Решение простейших дифференциальных уравнений

Дифференциальные уравнения - это уравнения, содержащие комбинации производных разного порядка зависимой переменной. Характерным примером такого уравнения является уравнение движения материальной точки в сильном поле F=F(x):

,

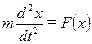здесь х- координата точки, t – время, m- масса.

Дифференциальные уравнения бывают линейными, когда неизвестная и ее производная представляют линейную комбинацию и нелинейным, когда неизвестные и ее производные входят в виде нелинейных зависимостей. Порядок старшей производной в уравнении определяет порядок дифференциального уравнения. Так, уравнение затухающих колебаний гармонического осциллятора является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами:

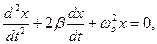
здесь х- смещение - 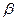коэффициент затухания, 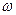_o-собственная частота осциллятора.

Дифференциальные уравнения, как правило, появляются при аналитическом решении различных физических задач. Решить дифференциальное уравнение означает найти явную зависимость зависимой переменной от ее аргумента. Ниже приводятся два метода решения простейших дифференциальных уравнений.

Метод разделения переменной.

Этот метод применяется в том случае, когда можно разделить зависимые и независимые переменные и разнести их в разные стороны уравнения.

Вот примеры таких уравнений:

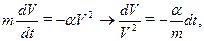
это уравнение описывает движение быстро движущихся тел в воздухе:

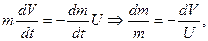
это уравнение описывает движение ракеты, здесь U -скорость истечения струи газа, 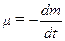- расход топлива.

В разделенных «дифференциальных» уравнениях левые и правые части зависят только от одной переменной. По этой причине их можно проинтегрировать независимо слева и справа и найти явный вид независимой переменной, как в случае уравнения:

,

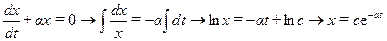здесь- с- некоторая постоянная.

Алгебраический метод.

Этот метод применим только к линейным дифференциальным уравнениям с постоянными коэффициентами:

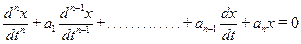
здесь а_i - постоянные величины.

В приведенном дифференциальном уравнении производные разного порядка связаны друг с другом линейной зависимостью. Подобной особенностью обладает экспоненциальная функция, в частности, выражение

.

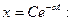
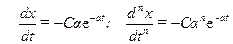Напрашивается мысль искать решение линейного дифференциального уравнения с постоянными коэффициентами в виде:

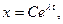
где с и 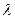- неизвестные постоянные величины. Проверим эту идею.

Подставляя предполагаемое решение в дифференциальное уравнение, производя необходимое дифференцирование и сокращение подобных сомножителей, получим обычные алгебраические уравнения:

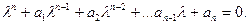
Корни этого уравнения λ_i имеют n- решений. Каждый корень определяет частные решения дифференциального уравнения:

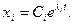
Суммой всех частных решений:

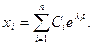
также является решением дифуравнения, и эта сумма есть его полное решение.

Неизвестные постоянные C_i, входящие в сумму находятся с помощью начальных или граничных условий конкретных физических задач.

Два приведенных метода решения дифференциальных уравнений являются эффектным инструментом при аналитическом решении простых задач физики. Реальный мир дифференциальных уравнений во много раз богаче и шире, а методы их решений тоньше и изощреннее. Но для решения задач механики первого курса университета, двух приведенных методов вполне достаточно.