Оценки для самоконтроля знаний
Результаты тестов:
По разделу «Кинематика» подсчитайте количество верных ответов на задачи из таблицы:
| Номера правильных ответов | Номера правильных ответов |
| 1.б) 2.а) 3.б),б),в) 4.б) 5.б) 6.б) 7.в) 8.в),а) 9.б,)в) 10.а) 11.а) 12.б) 13.а) 14.в) 15.а),б) 16.б) | 17.в) 18.в) 19.в) 20.б) 21.б),б) 22.б) 23.а) 24.б) 25.в) 26.в) 27.а) 28.б) 29.б) 30.а) 31.б) 32.в) |
Просуммируйте полученный результат и получите оценку в баллах:
от 1 до 13 верных ответов - 4 балла,
от 14 до 28 верных ответов – 8 баллов,
от 29 до 43верных ответов -10 баллов.
По разделу «Динамика материальной точки» подсчитайте количество правильных ответов на задачи, указанные в таблице:
| Номера правильных ответов | Номера правильных ответов | Номера правильных ответов |
| 1.б) 2.б) 3.а) 4.б) 5.б) 6.а) 7.б) 8.б)б) 9.а) 10.б) 11.б)б) 12.б)б) 13.а) 14.б) 15.в) 16.б) 17.в) 18.б)б) 19.б) 20.в) 21.в) 22.в)б) 23.в) 24.в) 25.в) | 26.в) 27.в)б) 28.в) 29.б) 30.в) 31.б) 32.б)а) 33.а) 34.а) 35.в) 36.б) 37.а) 38.в) 39.в) 40.в) 41.в)а) 42.в) 43.в) 44.б) 45.в) 46.б) 47.а) 48.а) 49.а) 50.б) | 51.в) 52.а) 53.а) 54.в) 55.в) 56.б) 57.в) 58.б) 59.в) 60.б) 61.в)б)а) 62.а) 63.в) 64.б)б) 65.в) 66.в) 67.в) 68.б)б)а) 69.б) 70.а) 71.б) 72.б) 73.б) 74.в) |
Просуммируйте полученный результат и получите оценку в баллах:
от 1 до 29 верных ответов - 4 балла,
от 30до 58 верных ответов – 8 баллов,
от 59 до 88 верных ответов -10 баллов.
Для подведения итога по разделу «Динамика твердого тела» подсчитайте количество правильных ответов на задачи из приведенной ниже таблицы:
| Номера правильных ответов | Номера правильных ответов |
| 1.б) 2.б) 3.б),а),б),а) 4.в),в) 5.а) 6.в) 7.в) 8.в) 9.а) 10.б) 11.в) 12.б) 13.в) 14.а),б) 15.в) 16.а) 17.б) 18.в) 19.а) 20.в) 21.б) 22.в) | 23.в) 24.б) 25.в) 26.а) 27.б) 28.в),а) 29.в) 30.в) 31.в) 32.в) 33.б) 34.а) 35.в) 36.в) 37.б) 38.б) 39.в) 40.в) 41.в) 42.в) 43.в) 44.в) |
от 1 до 17 верных ответов - 4 балла,
от 18 до 34 верных ответов – 8 баллов,
от 33 до 50 верных ответов -10 баллов.
Общая оценка определяется по сумме баллов по трем разделам:
от 4 до12 баллов – удовлетворительно,
от 14 до 22 баллов– хорошо,
от 24 до 30 – отлично.
Дополнительный материал
Векторная алгебра
Общие определения и свойства векторов.
Вектор- это геометрический объект, характеризуемый длиной и направлением. Визуально вектор можно представить как направленный отрезок.
Для задания произвольного вектора 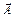 нужно задать три числа, которые называются его проекциями или компонентами. В декартовой системе координат вектор
нужно задать три числа, которые называются его проекциями или компонентами. В декартовой системе координат вектор 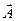 выражается через свои проекции
выражается через свои проекции 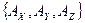 следующим образом:
следующим образом:
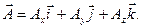
Геометрический смысл проекции на рисунке:
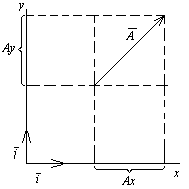
Длина вектора 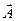 в декартовой системе координат равна:
в декартовой системе координат равна:
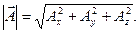
При переходе от одной декартовой системы координат (x,y,z) к другой (x`,y`,z`) вектор преобразуется: тройка чисел (Ax,,Ay,Az) переходит в новую тройку (A`x,,A`y,A`z). При этом преобразовании модуль или длина вектора 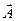 сохраняется:
сохраняется:
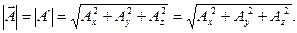
Равенство векторов
Два вектора 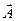 и
и 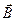 равны друг другу, если:
равны друг другу, если:
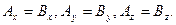
С геометрической точки зрения два вектора равны друг другу, если они имеют одну и ту же длину и направлены в одну и ту же сторону. Данное определение означает, что существует бесконечное большое число векторов равных некоторому вектору 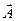 . Рисунок, представленный ниже, отражает это свойство векторов.
. Рисунок, представленный ниже, отражает это свойство векторов.
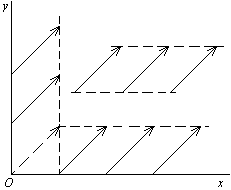
Все вектора на этом рисунке равны друг другу.
Параллельный перенос векторов
Как показывает рисунок, при параллельном переносе величина вектора 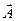 не изменяется.
не изменяется.
Векторные операции
Умножение вектора на скаляр
Операция 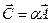 называется умножением вектора на скаляр. При такой операции длина вектора увеличивается в
называется умножением вектора на скаляр. При такой операции длина вектора увеличивается в 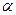 раз, а направление вектора сохраняется. В декартовой системе координат:
раз, а направление вектора сохраняется. В декартовой системе координат: 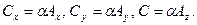
Сложение векторов
Суммой двух векторов 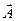 и
и 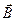 является новый вектор
является новый вектор 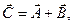 у которого проекции равны суммам соответствующих проекций векторов
у которого проекции равны суммам соответствующих проекций векторов 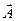 и
и 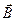 :
:
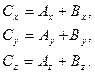
Геометрическим представлением сложения векторов является правило параллелограмма.
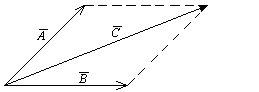
Вычитание векторов
Вычитание двух векторов является операция обратная сложению: 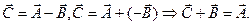
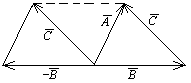
Геометрическим представлением вектора 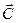 является вектор, соединяющий конец вектора
является вектор, соединяющий конец вектора 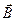 и
и 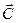 .
.
Скалярное произведение
Из двух векторов 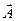 и
и 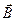 можно образовать скалярное произведение:
можно образовать скалярное произведение:
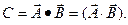
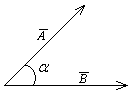
Величина скалярного произведения равна:
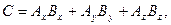
или 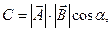 здесь
здесь 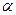 - угол между векторами
- угол между векторами 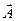 и
и 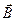 .
.
Векторное произведение
Операция векторного произведения из двух векторов 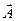 и
и 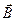 образует новый вектор:
образует новый вектор: 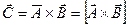 .Модуль векторного произведения равен
.Модуль векторного произведения равен 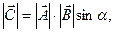 здесь
здесь 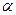 -угол между векторами
-угол между векторами 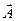 и
и 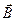 .
.
Геометрически модуль векторного произведения равен площади параллелограмма, построенного на векторах 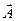 и
и 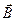 .
.
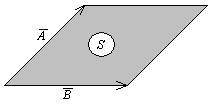
Направление векторного произведения определяется правилом правого винта: если головку винта вращать в плоскости векторов 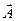 и
и 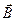 по кратчайшему направлению от вектора
по кратчайшему направлению от вектора 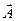 к вектору
к вектору 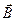 , то направление хода винта укажет направление вектора
, то направление хода винта укажет направление вектора 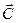 . Из этого определения следует, что вектор
. Из этого определения следует, что вектор 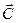 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 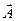 и
и 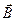 .
.
Проекции вектора 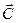 определяются с помощью определителя:
определяются с помощью определителя:
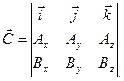
Откуда следует, что:
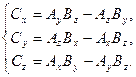
Основные векторные тождества:
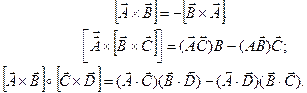
7.2.Таблицы производных и интегралов
| ФУНКЦИЯ | ПРОИЗВОДНАЯ |
| xn | nxn-1 |
| 1/x | -1/x2 |
| 1/xn | -n/xn+1 |
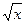
| 1/2 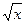
|
| eX | ex |
| exn | nenx |
| aX | ax lna |
| ln x | 1/x |
| sin x | cos x |
| cos x | - sin x |
| tg x | 1/cos2 x |
| ctg x | - 1/sin2 x |
| vu | u'/2vu |
| ln u | u'/u |
| u/v | (vu'-v'u)/v2 |
| arcsin x | 1/ 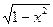
|
| arccos x | -1/ 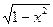
|
| arctg x | 1/(1+x2) |
| arcctg x | -1/(1+x2) |
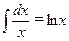 ;
; 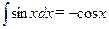 ;
;
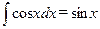 ;
; 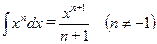 ;
;
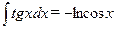 ;
; 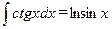 ;
;
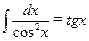 ;
; 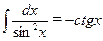 ;
;
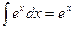 ;
; 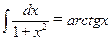 ;
;
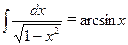 ;
; 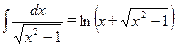 ;
; 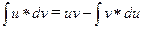 .
.
Дата добавления: 2020-10-25; просмотров: 572;











