Рекомендации по решению задач по механике с примерами решений
Решение типовых задач по механике не сложно. Как правило, эти задачи связаны с использование основных понятий механики и простых соотношений между ними. Примером такой задачи может быть следующее условие: показать, что при заданной скорости запуска диска спортсменом максимальная дальность полета достигается при угле пуска равном 45˚к горизонту. Для решения этой задачи достаточно помнить или найти в учебнике формулу для максимальной длины полета тела, брошенного под углом к горизонту. Применяя условие экстремума к функции, легко найти, что угол 45o отвечает максимуму длины.
Значительно сложнее решать задачи по механике, в которых решение не определяется готовыми формулами, а требует напряженных размышлений и глубокого понимания материала темы. Задачи такого плана в большом количестве даны в известном задачнике Московского физико-технического института: С.М.Козел, Э.И.Рашба, С.А.Славатинский «Сборник задач по физике». Переход от уверенного решения простых задач к столь же уверенному решению сложных является типичным примером развития творческих способностей студента. Он хорошо отражает общую тенденцию познания, когда человек переходит от понимания простого к пониманию сложного. Самое ценное при этом состоит в том, что на этом пути происходит постоянного накопления знаний и навыков, и приемы простых решений становятся составными шагами сложных. Сказанное означает, что приемы и алгоритмы решений как простых, так и сложных задач имеют общие основы или правила. Эти правила можно сформулировать так.
Правило 1. Успех решения задачи зависит от того, насколько глубоко поняты условия задачи.
Под пониманием подразумевается уверенные знания всех физических величин, входящих в условие задачи, а также ясное видение причинно-следственных связей между величинами задачи. Если по задаче нет ясных представлений ни о физических величинах, ни о функциональных связях между ними, необходимо открыть конспект лекций или учебник и внимательно прочитать нужный материал. Для поиска в учебнике нужного материала следует воспользоваться оглавлением и условиями задачи. Если в задаче фигурирует материальная точка, следует обратиться в разделы кинематики и динамики материальной точки. Если в условии идет речьо твердом теле, нужно открыть главы, посвященные кинематике и динамике твердого тела. И так следует поступать в любом случае, когда знаний на данный момент не хватает. Они появятся, но для этого придется напрячь мозги и потрудиться.
Правило 2. Для того, чтобы решить задачу, нужно построить логическую пошаговую схему, которая позволит перевести данные задачи в искомое решение. Примеры построения таких логических схем при решении задач повышенной трудности приведены в этом разделе.
Правило 3 (техническое). Решение задач, за редким исключением, должно производиться в алгебраических величинах. Это облегчает как саму процедуру вычислений, так и проверку правильности промежуточных шагов. Алгебраический подход позволяет также на каждом шаге задачи использовать метод размерностей для проверки промежуточных и окончательных выводов. При проведении численных вычислений нужно пользоваться правилом приближенных вычислений. В частности, точность вычислений должна соответствовать точности заданных исходных физических величин.
Объединяя два первых правила вместе, получим общий алгоритм решения задач по механике:
1. Строится физическая модель задачи, проводится при необходимости сведение ее к последовательности логически связанных подзадач, решение каждой из которых известно ранее, проводится объединение решений всех подзадач в окончательное решение.
2. Определяются ключевые понятия задачи и функциональные связи между ними. Фиксируются «внешние» условия задачи: характер движения физического объекта, замкнутость или разомкнутость физической системы, характер действующих в ней сил: потенциальных или нет, следствия из этих условий и т.д.
3. Строится логическая схема решения, проводится при необходимости сведение ее к последовательности логически связанных подзадач, решение каждой из которых известно ранее, проводится объединение решений всех подзадач в окончательное решение.
Ниже на примере решения трех задач повышенной трудности дана демонстрация того, как ищется решение в соответствии с приведенным алгоритмом. Три других примера конструирования решений даны в разделе 5 «Задачи-оценки».
Задача 1
С колеса движущегося автомобиля соскакивает декоративный колпак, который, попрыгав по дороге, начинает катиться без скольжения. При какой скорости автомобиля Vo это возможно? Радиус колеса равен R= 40 см, колпак можно рассматривать как однородный диск радиусом r=20 см, коэффициент трения между колпаком и дорогой k= 0,2.
1.Физическая модель задачи
Вначале колпак движется с колесом с поступательной скоростью Vo и угловой скоростью вращения 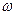 o=Vo /R. После срыва центра масс колпак падает с высоты (R-r) на дорогу и начинает подскакивать, испытывая с дорогой неупругие столкновения.
o=Vo /R. После срыва центра масс колпак падает с высоты (R-r) на дорогу и начинает подскакивать, испытывая с дорогой неупругие столкновения.
В каждый момент контакта с землей на колпак действуют две силы: трение скольжения и реакция поверхности, равная по величине и противоположная по направлению силе давления колпака на поверхность. Эффекты от действия этих сил легко определить из рисунка.
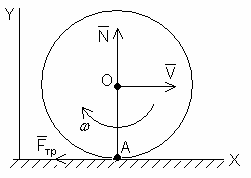
Как видно из рисунка, сила трения замедляет поступательное движение колеса, одновременно ускоряя его вращательное движение, так как момент этой силы направлен в направлении вращения.
Из-за неупругого взаимодействия колпака с дорогой после каждого удара подскок колпака становится ниже и ниже, и, наконец, подпрыгивание прекращается. Это означает, что вся потенциальная энергия, которой колпак обладал вначале- израсходована, вместе с ней была потеряна и часть энергии поступательного движения за счет действия силы трения.
2 Основные понятия
Качение без проскальзывания, неупругие столкновения, сила трения скольжения, момент силы трения, сила реакции, сила давления, уравнение движения твердого тела.
Качение без проскальзывания это движение колеса, в данной задаче колпака, когда в точке контакта колеса и поверхности, скорость колеса равна нулю. Это означает, что нет скольжения одного тела относительно другого. При качении без проскальзывания колпака скорость его центра масс связана с угловой скоростью вращения соотношением:
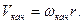
При проскальзывании это условие не выполняется и 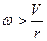 , или
, или 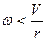 .
.
Сила трения скольжения равна 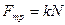 , где N - сила давления, равная и противоположная по направлению силе реакции опоры. Сила давления в общем случае зависит от характера взаимодействия тел. В частности, в данной задаче она зависит от вертикального импульса центра масс колеса. Связь всех названных физических величин задачи задается уравнением движения твердого тела:
, где N - сила давления, равная и противоположная по направлению силе реакции опоры. Сила давления в общем случае зависит от характера взаимодействия тел. В частности, в данной задаче она зависит от вертикального импульса центра масс колеса. Связь всех названных физических величин задачи задается уравнением движения твердого тела:
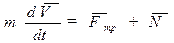 ,
,
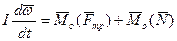 ,
,
где m и I-масса и момент инерции колпака, t- время,
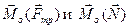 - моменты сил трения и реакция опоры относительно центра масс колпака.
- моменты сил трения и реакция опоры относительно центра масс колпака.
3.Логическая схема решения
Запишем уравнения движения колпака в координатных осях x, y и z (ось z проходит через центр масс колеса):
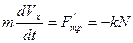 ,
, 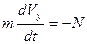 ,
, 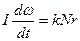 .
.
В приведенных формулах все обозначения соответствуют рисунку. Момент силы реакции в последнее уравнение не входит, так как он равен нулю.
Разделим первое уравнение на второе. В результате получим:
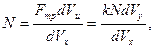
или
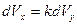 .
.
Проинтегрируем полученное уравнение в пределах изменения скорости V x от Vo до Vкач , а Vy от Vyo до нуля.
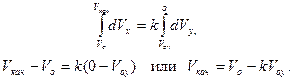
Так как центр масс колпака падает с высоты (R-r), то Voy равна:
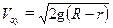 .
.
Окончательно:
 .
.
Свяжем теперь поступательную скорость движения колпака с его угловой скоростью. Для этого разделим первое уравнение системы на третье. Получим,
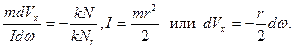
Проинтегрируем левую часть уравнения в пределах от Vo до Vкач , а правую часть от 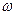 o до
o до 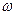 кач
кач
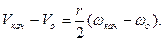
Учитывая, что:
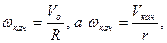
получим:
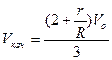 .
.
Теперь объединим промежуточные результаты
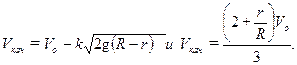
Выделяя Vo , имеем:
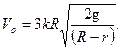
. Подставим в последнее выражение численные значения, найдем, что подобное движение колпака возникает при 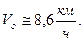
Задача 2
Пуля массой m, летящая горизонтально со скоростью V0 , попадает в покоящийся на шероховатом горизонтальном столе деревянный шар массой М и радиусом R на расстоянии l ниже центра масс шара и застревает в нем. Найти установившуюся скорость V шара. Считать, что m<<M.
1.Построение физической модели
Для построения физической модели задачи воспользуемся близким по характеру примером из бильярда. Как известно, при ударе кием по бильярдному шару, тот начинает катиться по поверхности стола. Импульс и момент вращения, кинетическая энергия шара возникли в результате столкновения кия с шаром. С учетом изложенного, картину столкновения пули и шара можно описать так. Быстролетящая пуля проникает в деревянный шар, тормозится и передает свой импульс, энергию и момент импульса шару. Так как удар неупругий, то механическая энергия не сохраняется, часть ее тратится на преодоление сил сопротивления материала. Полный импульс и момент импульса системы, напротив, сохраняются, так как для этих законов сохранения нет таких жестких ограничений как действие потенциальных сил. Важный момент данной задачи - скоротечность столкновения пули с шаром. Процесс проникновения и торможения пули происходит за десятые доли миллисекунды. За это время центр масс шара не успевает сколько-нибудь заметно сместиться из-за закона инерции. Второй важный момент задачи - учет шероховатости поверхности, который означает необходимость учета силы трения на начальном этапе движения шара. Эта сила может быть силой скольжения, если происходит качение шара с проскальзыванием, или сила трения качения, если проскальзывания нет.
2. Основные понятия задачи
В соответствии с физической моделью, имеем последовательность явлений:
1) неупругое столкновение пули с шаром с полной передачей импульса и момента вращения;
2) качение шара после столкновения при действии силы трения и заданных начальных условиях.
Для описания этих явлений необходимо знание:
1) импульса и момента импульса пули:
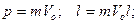
2) импульса и момента импульса шара:
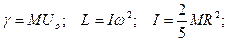 ;
;
3) условия непроскальзывания шара:
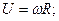
4) уравнений движения твердого тела:
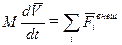 ,
,
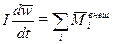 .
.
3. Логическая схема решения
В соответствии с физической моделью, данную задачу можно разбить на две подзадачи: столкновение и качение.
Описание столкновения. При столкновении пули и шара сохраняется полный импульс и момент импульса системы. Математически это выглядит так:
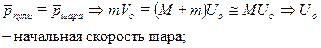
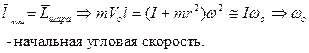

При написании последнего уравнения учтено, что ось вращения проходит через центр масс шара и параллельна плоскости качения.
Итак, сразу же после столкновения центр масс шара движется со скоростью -
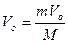 ,
,
а сам шар вращается с угловой скоростью-
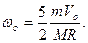
Легко видеть, что

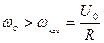 .
.
Это означает, что качение тела начинается с проскальзывания.
Описание качения
Эта подзадача во многом повторяет задачу о качении колеса (см. задачу 1). Поэтому, воспользуемся пояснениями предыдущей задачи.
Уравнения движения шара после столкновения:
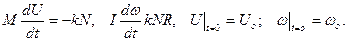
Разделим первое уравнение на второе:
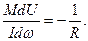
Преобразуем это уравнение к виду удобному для интегрирования:
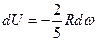
и проинтегрируем в пределах от Uo до Uкач и от 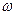 o до
o до 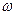 кач .
кач .
При интегрировании необходимо учесть один нюанс. Он связан с тем, что знаки 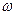 0 и
0 и 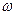 кач разные. Это показано на рисунке:
кач разные. Это показано на рисунке:
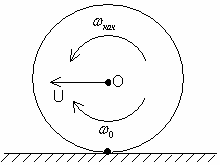
С учетом сказанного:
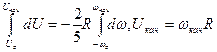 ,
,
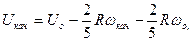
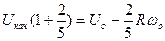 ,
,
 .
.
Задача 3
По направлению к Земле из глубины космоса движется метеоритное облако, скорость которого на значительном удалении от Земли равна Vo=5км/с. Поперечные размеры этого облака много больше диаметра Земли, (толщина облака по направлению движения) составляет h=1000 км, средняя концентрация метеоритов n=0,1 км-3, а центр облака движется в направлении центра Земли. Найти общее число N метеоритов, которые попадут не Землю.
1.Физическая модель
На Землю попадут все метеориты, траектории которых пересекутся с Землей. Одни из них упадут на Землю, двигаясь практически прямолинейно, другие столкнутся
С Землей, потому что их траектории будут искривлены притяжением планеты. Качественно характер траекторий метеоритов, которые упадут на Землю можно изобразить рисунком.

Из рисунка следует, что все метеориты, находящиеся в цилиндрической области облака с радиусом Ro и длиной h, попадут на Землю. Поверхность вращения, которая образуется вращением предельной траектории dd’ вокруг линии аа’, разграничивает две области метеоритов. Те которые лежат внутри этой поверхности - падают на Землю, те которые вне ее - облетают нашу планету и затем летят вспять.
1.Основные понятия
Может показаться, что основным понятием данной задачи будет сила гравитационного взаимодействия метеоритов и Земли, так как она искривляет траектории метеоритов, притягивая их к Земле. Однако решение этой задачи обходится без рассмотрения силы гравитации. Дело в том, что характер траекторий небесных тел, движущихся в поле тяготения силового центра (Солнца или Земли в данной задаче), определяется параметром орбиты и ее эксцентриситетом. Что это за величина можно узнать, заглянув в учебник А. Н. Матвеева “Механика и теория относительности” в разделе “Движение планет и комет”, тогда выяснится, что параметр орбиты и эксцентриситет определяются полной механической энергией и моментом импульса планет и комет. Сохранение же полной механической энергии и момента импульса при движении в потенциальном и центральном силовом гравитационном поле, обеспечивает каждую орбиту планеты или кометы своеобразной родовой меткой: на определенной орбите могут находиться только тела с фиксированными значениями полной механической энергии. Полная механическая энергия Е метеорита в поле тяготения Земли равна:
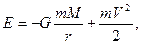
здесь r – расстояние от центра Земли до метеорита, m и M- масса метеорита и Земли, V - скорость метеорита относительно Земли.
Момент импульса l – метеорита относительно системы отсчета, связанной с центром земли равен:
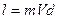 ,
,
где d - прицельный параметр – кратчайшее расстояние между направлением вектора скорости и центром Земли.
Сохранение полной механической энергии задается условием:
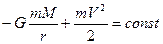 ;
;
сохранение момента импульса
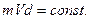
1.Логическая схема решения
Обратимся к рисунку, на котором изображены траектории движения метеоритов. Одна из этих dd’ является особой. Она разделяет траектории, пересекающиеся с Землей, и, проходящие мимо Земли. Применим к этой траектории законы сохранения полной механической энергии для точек d и d’:
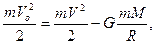
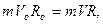
здесь R - радиус Земли.
Разрешая эту систему, найдем Ro:
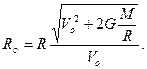
Теперь не составляет большого труда найти число метеоритов, попадающих на Землю. Оно будет равно, как отмечалось выше, числу метеоритов, находящихся внутри цилиндра радиусом Ro и длиной h,
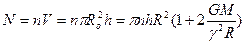 .
.
4. Качественные задачи-оценки
Задачи-оценки – это задачи, в которых все необходимые физические величины студент должен задать сам. Для решения таких задач не требуется высшая математика, но зато необходимы уверенные знания основ механики и физическая интуиция. Решение задач-оценок в определенной степени воспроизводит творческий подход профессионалов-физиков при первичном анализе новых явлений. Поэтому эти задачи можно рассматривать как первую «пробу на зубок» для тех, кто хочет в будущем серьезно заниматься физикой. Ниже предлагается несколько задач-оценок. Три из них сопровождены поясняющими решениями, остальные предназначены для самостоятельной работы.
Задача 1
Оценить силу сопротивления воздуха, которую испытывает автомобиль при движении со скоростью V.
Разобьем задачу на ряд шагов.
Шаг первый. Надо дать ответ на вопрос: почему воздух препятствует движению? Ответ на него прямо связан с понятием силы и вторым законом Ньютона. По второму закону Ньютона сила:
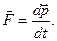
При постоянной скорости автомобиля его импульс не меняется, но сила сопротивления действует. Это означает, что должен меняться импульс набегающего на автомобиль воздуха. Ответим на вопрос: почему он меняется? При обтекании автомобиля воздух меняет свою скорость и направление движения. Это и приводит к изменению импульса. Теперь остается количественно описать это изменение.
Шаг второй. Перейдем к количественным оценкам силы сопротивления. Для этого представим второй закон Ньютона в виде отношения конечных приращений:
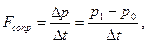
здесь p1 – импульс воздуха после прохождения автомобиля;
pO - импульс набегающего воздуха до прохождения; 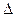 t- время обтекания. Предположим для простоты, что после взаимодействия с поверхностью автомобиля воздух остановился. Тогда:
t- время обтекания. Предположим для простоты, что после взаимодействия с поверхностью автомобиля воздух остановился. Тогда:
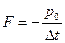 .
.
Найдем величину импульса po набегающего воздуха, помня о том, что это воздух, который обтекает автомобиль за время. 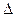 t. Очевидно, что это количество воздуха будет по величине близко к массе воздуха, который автомобиль вытеснит на своем пути. За время
t. Очевидно, что это количество воздуха будет по величине близко к массе воздуха, который автомобиль вытеснит на своем пути. За время 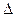 t автомобиль пройдет расстояние v
t автомобиль пройдет расстояние v 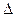 t и вытеснит воздух, который находится внутри объема
t и вытеснит воздух, который находится внутри объема 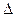 V,
V, 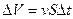 , где S – поперечное сечение автомобиля. Масса этого набегающего воздуха будет равна:
, где S – поперечное сечение автомобиля. Масса этого набегающего воздуха будет равна:

где 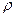 – плотность воздуха, а импульс:
– плотность воздуха, а импульс:
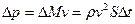 .
.
Подставим полученное соотношение в выражение для силы и найдем оценочно силу сопротивления Fсопр:
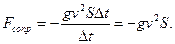
Шаг третий. Проанализируем полученное выражение. Основной вывод, который напрашивается, заключается в том, что сила сопротивления пропорциональна квадрату скорости. Другой вывод связан с зависимостью силы сопротивления от площади поперечного сечения. Эта сила тем меньше, чем меньше поперечные габариты автомобилей. По этой причине спортивные болиды делаются приземистыми и обтекаемыми.
Задача 2
Оценить частоту звучания скрипичной струны и зависимость ее от натяжения и плотности материала.
Шаг первый. Выясним, почему «поет» струна. Ответ прост. Для этого достаточно понаблюдать «пение» струны и придти к заключению, что причиной «пения» является колебание струны: струна «поет», когда есть колебания, и «молчит», когда их нет. Теперь остается сделать следующий шаг – оценить частоту колебаний струны и связать ее с частотой звуковых волн, возбуждаемых этими колебаниями.
Шаг второй. Для приближенного нахождения частоты колебаний закрепленной струны следует построить простейшую модель деформации струны смычком. Предположим, что смычок касается струны в ее середине. При движении смычка за счет сил трения струна будет увлекаться за смычком и деформироваться. В результате деформации струна примет следующую форму:
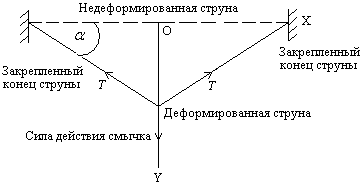
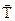 - сила натяжения струны.
- сила натяжения струны.
Шаг третий. Поставим вопрос: насколько сильно может деформироваться струна? Ответ на этот вопрос связан с соотношением сил деформации и действия смычка. Последняя, при отсутствии проскальзывания смычка, есть не что иное, как сила трения покоя. Итак, одна сила может нарастать без особых ограничений, а другая имеет предел в виде силы трения скольжения. Что может произойти в этом случае? Конечно же, срыв струны. Причем, срыв произойдет тогда, когда параметр деформации струны у достигнет некоторого максимального значения 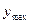 .
.
Шаг четвертый. Найдем характерное время возвращения струны в равновесное положение, когда после срыва на нее действует только сила деформации. Для простоты оценок будем считать, что вся масса струны собрана в ее центре. Как видно из рисунка, на эту массу в направлении y будет действовать результирующая сила равновесия:
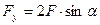 ,
,
здесь F – сила натяжения. Сделаем новое предположение относительно силы натяжения. Это предположение основано на реальной практике: струна «поет» тем лучше, чем сильней она натянута изначально. С учетом того, что амплитуда колебаний мала (смещение струны скрипки трудно заметить невооруженным глазом), делаем другое предположение: при деформации струны сила натяжения возрастает, но ее величина остается близкой к величине начальной силы натяжения. Сказанное означает, что при деформации струны силу натяжения можно считать постоянной, а угол 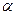 настолько малым, что
настолько малым, что 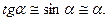
Теперь мы обладаем необходимой информацией, чтобы рассчитать время возвращения струны в положение равновесия.
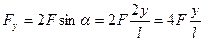
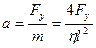
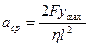
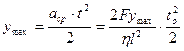
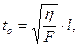
здесь F – сила натяжения; l - длина; 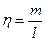 – линейная плотность материала струны;
– линейная плотность материала струны; 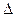 t– характерное время возвращения струны в равновесное положение.
t– характерное время возвращения струны в равновесное положение.
Шаг пятый. Расчет характерной частоты «пения» струны. Вспомним, что это возмущения давления и плотности воздуха. При движении струны такие возмущения должны повторяться с периодичностью 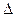 t, причем они будут максимальными, когда струна будет проходить положение равновесия, и ее скорость будет максимальной. Остается теперь связать период возмущений давления воздуха с характерной частотой звуковых волн:
t, причем они будут максимальными, когда струна будет проходить положение равновесия, и ее скорость будет максимальной. Остается теперь связать период возмущений давления воздуха с характерной частотой звуковых волн:
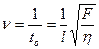 .
.
Шаг шестой. Анализ полученного результата.
Формула для характерной частоты звучания струны указывает на три принципиальные зависимости:
-частота зависит от силы натяжения как F1/2,
- частота зависит от линейной плотности как 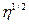 ;
;
- частота обратно пропорциональна длине струны.
Все эти зависимости используются в струнных инструментах для того, чтобы их игра была богаче и выразительнее.
Задача 3
Оценить температуру, до которой может, разогреется протозвезда при сжатии. Начальный радиус протозвезды R1 , конечный-R2 . Масса звезды M однородно распределена по шаровому объему. Полученный результат применить для оценки температуры внутри Солнца.
Первый шаг. Выясним, почему при сжатии протозвезд (больших по размерам и массе образованиям космической пыли) происходит разогрев вещества. Для этого вспомним, что температура – это мера теплового или хаотического движения атомов в газообразной среде. В частности, тепловая кинетическая энергия частиц идеального газа равна:
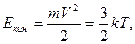
здесь m и V-масса и средняя тепловая скорость движения частиц, k- постоянная Больцмана, T- температура в градусах Кельвина. Из приведенной формулы следует, что температура идеального газа тем выше, чем больше по величине скорость теплового движения частиц. Так как при сжатии протозвезды температура вещества повышается, существует механизм увеличения кинетической энергии теплового движения частиц. Этот механизм должен быть связан с действием сил гравитации, работа которых может изменить кинетическую энергию частиц. Эта сила стремится стянуть вещество протозвезды к некому центру, который можно условно назвать ядром будущей звезды. При сжатии вещества протозвезды гравитационные силы совершают положительную работу, которая и переходит в конечном итоге в кинетическую энергию теплового движения частиц. В чем-то процесс увеличения кинетической энергии теплового движения частиц протозвезды похож на возрастание энергии свободно падающего на землю тела, хотя сам процесс перехода гравитационной энергии частиц в их кинетическую энергию значительно сложнее. Также значительно сложнее сама физика сжимающихся протозвезд, в которых процесс сжатия развивается при конкуренции сил гравитации и теплового давления, порождаемого все тем же тепловым движением частиц.
Шаг второй. Оценим работу, которую совершают силы гравитации сжатии протозвезды. Для этого представим шарообразную звезду как объект состоящий из двух половин –полушаров равной массы M/2, которые находятся на расстоянии R/2 друг от друга. Выбор расстояния в половину радиуса протозвезды обусловлен тем, что основная масса полушаров находится поближе к большому диаметру полушаров, нежели к их периферии. Для оценки потенциальной энергии гравитационного взаимодействия двух полусфер воспользуемся известной формулой для потенциальной энергии притяжения двух точечных масс, находящихся на расстоянии друг от друга. В результате получим приближенное соотношение:
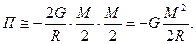
Отметим, что полученное нами выражение очень близко по величине к точному выражению собственной потенциальной гравитационной энергии однородного шара, равной:
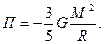
Найдем работу, которую совершает гравитация при сжатии протозвезды. Для этого воспользуемся связью между работой и потенциальной энергией:
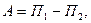
здесь П1 и П2 –потенциальная энергия в начальном и конечном состоянии системы. Применительно к сжатию протозвезды:
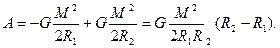
Шаг третий. Свяжем теперь работу сил гравитации с применением кинетической энергии вещества протозвезды. Как известно, приращение кинетической энергии равно работе  отсюда следует, что:
отсюда следует, что:
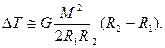
Насколько это выражение верно - предлагаем разобраться самостоятельно, подсказкой будет теорема о вириале, о которой можно прочесть в книге Ч. Кителя, У. Найта и М. Рудермана «Берклиевский курс физики. Механика».
Предположим далее, что все изменения кинетической энергии вещества протозвезды перешло в энергию теплового движения частиц.
Полная тепловая энергия вещества протозвезды равна:
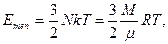
здесь N - полное число частиц, 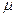 - молярная масса вещества протозвезды, R-универсальная газовая постоянная, Т-температура.
- молярная масса вещества протозвезды, R-универсальная газовая постоянная, Т-температура.
Изменение тепловой энергии в свою очередь равно изменению кинетической энергии вещества протозвезды:
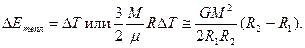
В итоге:
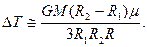
Шаг четвертый. Оценим температуру внутри ближайшей звезды – Солнца, считая, что начальный радиус протоСолнца была много больше настоящего значения, а масса Солнца не изменилась сильно за время своего существования.
Так как 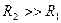 , то
, то
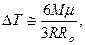
здесь Ro – радиус Солнца. Молярная масса 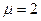 с учетом того, что Солнце на 60% состоит из водорода и на 40% из гелия. Масса и радиус Солнца равны соответственно:
с учетом того, что Солнце на 60% состоит из водорода и на 40% из гелия. Масса и радиус Солнца равны соответственно:
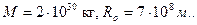
В результате получаем:
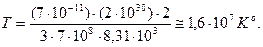
Полученное значения температуры Солнца близко к тому, что получается при более точных расчетах и определяется на основе измерения потока нейтрино от Солнца. Это говорит об обоснованности наших упрощенных оценочных расчетов и правильности выбранных модельных представлений.
Задачи-оценки для самостоятельного решения.
Задача 1. Оценить силу натяжения тросов парашюта в момент раскрытия и скорость опускания парашютиста после раскрытия.
Задача 2. Оценить глубину ямы на поверхности воды под вертолетом, зависшим над озером на небольшой высоте.
Задача 3. Оценить наименьшую скорость, с которой можно ехать на водных лыжах.
Задача 4. Оценить давление в центре Земли.
Задача 5. Оценить силу натяжения цепи велосипеда при езде в гору.
Задача 6. Оценить различие в расстоянии от уровня мирового океана до центра Земли на полюсе и на экваторе, вызванное вращением Земли.
Задача 7. Оценить давление, создаваемое острием швейной иголки, поставленной вертикально на письменный стол, покрытый стеклом, если стукнуть по ней молотком.
Задача 8. Оценить, на какой высоте лопнет воздушный шарик, наполненный гелием.
Задача 9. Оценить время столкновения двух воздушных шаров.
Задача 10. Оценить время колебаний дождевой капли.
5. Тестовые задачи
КИНЕМАТИКА
I. Точка движется по окружности радиусом R и совершает один оборот. Чему равны перемещение и путь, пройденные точкой?
| а) | 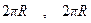 ; ;
|
| б) |  . .
|
2. Частица движется с постоянной скоростью V по окружности радиуса R. Чему равны тангенциальное, нормальное и полное ускорение?
| а) | 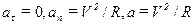 ; ;
| |
| б) | 
| |
3. Математический маятник совершает колебания с угловой амплитудой 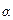 . Чему равно нормальное ускорение в крайнем положении?
. Чему равно нормальное ускорение в крайнем положении?
| а) | 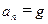 ; ;
|
| б) | 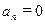 . .
|
Чему равно тангенциальное ускорение в этой точке?
| а) | 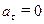 ; ;
|
| б) | 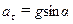 . .
|
Чему равно нормальное ускорение в положении равновесия?
| а) |  ; ;
|
| б) | 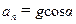 ; ;
|
| в) | 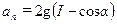 . .
|
4. Ускорение частицы равно нулю, если:
| а) | Модуль скорости 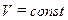 ; ;
|
| б) | Скорость частицы 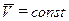 . .
|
5. Может ли тело в один и тот же момент времени иметь равную нулю скорость и не равное нулю ускорение?
| а) | Нет; |
| б) | Да. |
6. Человек, стоящий на крае обрыва бросает вертикально вверх камень со скоростью V. Второй камень он бросает вниз с той же скоростью. Упадет ли второй камень к подножию обрыва с большей скоростью? Сопротивлением воздуха пренебречь.
| а) | Да; |
| б) | Нет. |
7. Положение тела х дается выражением x=At+4Bt3 , где А и В - константы, t - время. Чему равно ускорение тела в зависимости от времени?
| а) | 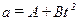 ; ;
|
| б | 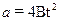 ; ;
|
| в) | 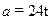 . .
|
8. Зависимость радиус-вектора 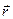 частицы от времени дается законом:
частицы от времени дается законом:
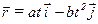 ,
,
где a, b - константы,  и
и 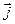 - единичные орты.
- единичные орты.
Уравнение траектории частицы дается выражением:
| а) | 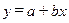 ; ;
|
| б) | 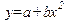 ; ;
|
| в) |  . .
|
Модуль скорости движения частицы дается выражением:
| а) | 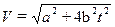 ; ;
|
| б | 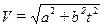 ; ;
|
| в) | 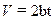 . .
|
9. Точка движется по окружности радиуса R так, что зависимость пути S от времени дается формулой:
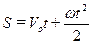 .
.
Тангенциальное ускорение aτ точки равно:
| а) | 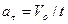 ; ;
|
| б) | 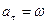 ; ;
|
| в) | 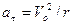 . .
|
Полное ускорение точки равно:
| а) | 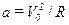 ; ;
|
| б) | 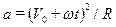 ; ;
|
| в) | 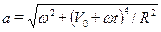 . .
|
10. Точка движется по окружности. Может ли вектор ускорения быть направлен под углом отличным от нуля к касательной в данной точке?
| а) | Да; |
| б) | Нет. |
11. Точка движется по некоторой кривой, имея постоянные по модулю скорость и ускорение. Форма кривой определяется как:
| а) | Окружность; |
Дата добавления: 2020-10-25; просмотров: 693;











