Внутренняя (полная) удельная поверхностная энергия

При образовании единицы поверхности S изменяется внутренняя поверхностная энергия.

Вернемся к объединенному уравнению первого и второго начал химической термодинамики для этого случая:

dU=TdS – pdV + σds +Σ μ_idn_i + φ dq (2.27)

где S – энтропия, μ_i – химический потенциал компонента, φ – потенциал поверхности.

При неизменном объеме системы V, постоянном составе вещества n, отсутствии заряда q на поверхности (V, n, q = const) получаем:

dU=TdS + σds. (2.28)

Проинтегрируем полученное уравнение от s до (s+1) (при образовании единичнгой поверхности):

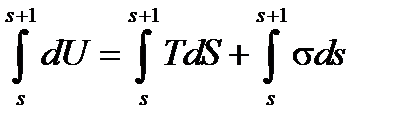, (2.29)

получаем: U_S= TS_S + σ, (2.30)

где σ = G_S, а TS_S = q_s– скрытая теплота образования единицы поверхности, величина q_s всегда >0.

Внутренняя поверхностная энергия единицы поверхности больше поверхностной энергии Гиббса^(*) на теплоту образования единицы поверхности. Поэтому ее обычно называют полной поверхностной энергией.

Запишем уравнение для изобарно-изотермического потенциала в дифференциальной форме:

dG= SdT –VdP, (2.31)

где S – энтропия системы; Т – температура, V – объем, P – давление.

Из этого уравнения следует, что температурная зависимость энергии Гиббса:

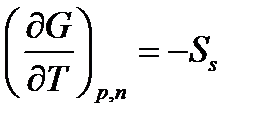; а т.к. σ = G_S_,то и 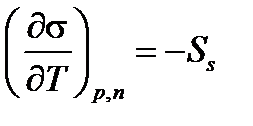(2.32)

Отсюда q_s = TS= 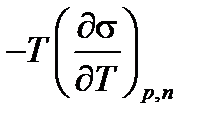(2.33)

Для конденсированных систем из-за очень небольшой разницы в объемах полная внутренняя энергия U и энтальпия Н практически совпадают, поэтому уравнение Гиббса-Гельмгольца^(**), связывающее полную поверхностную энергию или энтальпию с энергией Гиббса в этом случае можно записать:

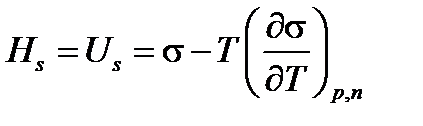. (2.34)

Как следует из уравнения (2.34), для определения U_s или Н_s надо знать σ и зависимость σ = f(Т). Конкретную зависимость можно определить только экспериментально.

Значения U_s, Н_s, q_s для некоторых веществ приведены в табл. 2.3.

Таблица 2.3

<7 8 91011 12 13 >

Дата добавления: 2016-07-27; просмотров: 3097;