Показатели силы влияний

Определение силы влияний по их результатам требуется в биологии, сельском хозяйстве, медицине для выбора наиболее эффективных средств воздействия, для дозировки физических и химических агентов – стимуляторов, замедлителей, возбудителей, лекарственных препаратов, пищевых средств.

Измерение силы статистического влияния может быть произведено при помощи квадрата корреляционного отношения, предложенного К. Пирсоном, – показателя, который может измерять силу влияния одного признака на другой при любой форме корреляционной связи.

Такое использование корреляционного отношения стало возможным потому, что в основу этого показателя К. Пирсон положил отношение величин, которые в настоящее время определяются как дисперсии – факториальная (межгрупповая) и общая, т. е. как основные элементы дисперсионного анализа.

При дисперсионном анализе ортогональных комплексов используются аддитивные свойства частных дисперсий (сумм квадратов центральных отклонений):

С_V + С_Z = С_Y, С_А + С_B + С_АВ + С_Z = С_Y.

На этом свойстве аддитивности частных дисперсий основан описанный выше закон разложения общих дисперсий в ортогональных комплексах.

Если взять отношения частных дисперсий к общей:

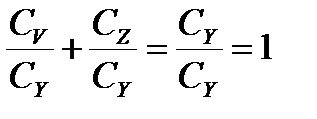; (15.13)

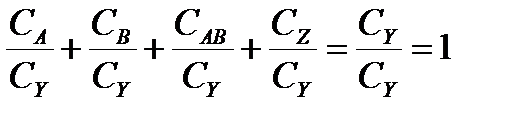, (15.14)

Каждое из этих отношений будет показывать долю участия отдельной частной дисперсии в образовании общей дисперсии.

А так как каждая частная дисперсия соответствует одному из частных влияний, то отношение частной дисперсии к общей измеряет долю данного влияния в общем суммарном статистическом влиянии всех факторов определяющих развитие данного результативного признака.

Поэтому доля (выраженная в относительных единицах или в процентах) каждой частной дисперсии в общей их сумме может быть принята за показатель силы влияния, того влияния, которое характеризуется данной частной дисперсией – или одной из факториальных или случайной.

Например, в однофакторном комплексе, чем большую долю в общей дисперсии занимает ее факториальная часть (С_V/С_Y), тем большая часть общего разнообразия обусловлена разнообразием градаций фактора, а это и означает, что фактор действует с большей силой, оставляя на долю случайных влияний меньшую часть общего разнообразия признака.

Таким образом, сила влияния фактора (факторов) в дисперсионном анализе измеряется отношением дисперсий частных к общей:

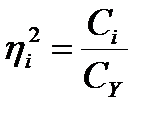(15.15)

Так как этот показатель отражает основной закон разложения общих дисперсий и основное аддитивное свойство частных дисперсий, а также составлен из основных элементов дисперсионного анализа, то отношение одной из факториальных дисперсий (С_V, С_А, С_B, С_АB) или случайной дисперсии (C_Z) к общей (С_Y) можно назвать основным показателем силы влияний факторов – организованных и неорганизованных.

Квадратный корень из основного показателя силы влияния в однофакторных комплексах 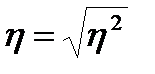есть пирсоновское корреляционное отношение, символ которого η перешел и на современный показатель, силы влияния.

В однофакторном комплексе определяются два показателя силы влияния: организованного фактора:

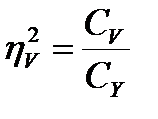(15.16)

и неорганизованного фактора:

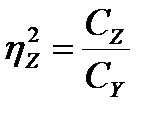(15.17)

Сумма этих показателей равна единице:

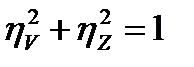(15.18)

В двухфакторном комплексе определяются пять видов влияний:

1 Влияние первого фактора:

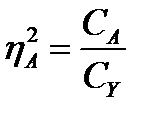(15.19)

2 Влияние второго фактора:

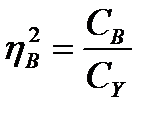(15.20)

3 Влияние сочетаний градаций обоих факторов:

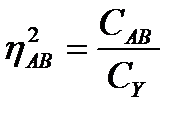(15.21)

4 Суммарное действие обоих факторов:

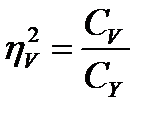(15.22)

5 Действие случайных факторов:

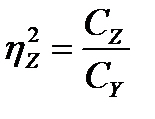(15.23)

Интерпретация показателей 4-го и 5-го влияний в двухфакторном дисперсионном комплексе проводится так же, как и в однофакторном: комплексе: чем больше 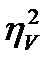, а значит, чем меньше 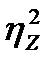, тем сильнее проявилось суммарное действие обоих организованных факторов.

Интерпретацию первых трех влияний в двухфакторном комплексе лучше начинать с показателя влияния сочетаний градаций.

Этот показатель 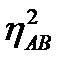всегда настолько больше нуля, насколько сильно действие одного фактора зависит от действия (градаций) другого.

Наименьшее значение этого показателя 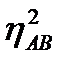=0 получается, когда один фактор действует совершенно одинаково при любых градациях второго.

Наибольшее значение этого показателя равно показателю суммарного влияния организованных факторов: 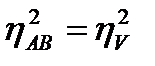. Так может получиться, когда действие одного фактора при одной градации второго фактора строго противоположно его действию при других градациях второго фактора.

В таких крайних случаях получаются очень малые показатели частных влияний первого фактора 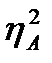или второго 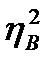, или того и другого – они приближаются к нулю, но это не связано со слабым действием каждого фактора в отдельности.

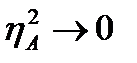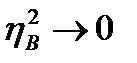
При , 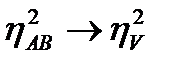действие одного фактора настолько сильно зависит от действия другого, что становится невозможным изучать и использовать влияние первого фактора без учета влияния второго.

Показатели силы влияния каждого фактора в двухфакторном комплексе 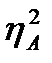и и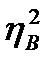меют особое значение, зависящее от силы сочетания их градаций: .

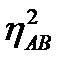Если показатель сочетания градаций не велик 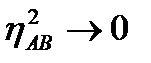, то показатели частных влияний факторов ( 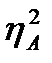и 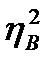) имеют обычное значение: чем они больше, тем сильнее влияние фактора.

Надо только помнить, что сила каждого фактора в отдельности измеряется в дисперсионном комплексе при усредненном действии градаций другого фактора, что равносильно известному требованию изучать варианты воздействий «при прочих равных условиях».

В тех же случаях, когда возрастает влияние сочетания градаций обоих факторов ( 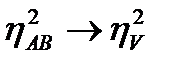), уже нельзя по показателям ( 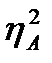и 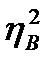) судить в полной мере о силе соответствующих влияний. Как указывалось, в таких случаях возможны очень малые показатели силы статистического влияния каждого фактора в отдельности при очень заметном их физиологическом влиянии на результативный признак.

В таких случаях сильное действие одного фактора имеет противоположное направление в разных градациях другого фактора. При усреднении таких противоположных действий получается в большей или меньшей степени нивелировка измерений силы влияния, что и приводит к уменьшению показателей силы частного влияния каждого фактора в отдельности.