Алгоритм дискриминантного анализа

Решение задач дискриминации (дискриминантный анализ) состоит в разбиении всего выборочного пространства (множества реализации всех рассматриваемых многомерных случайных величин) на некоторое число областей.

Пусть имеются две генеральные совокупности X и Y, имеющие многомерный (трехмерный) нормальный закон распределения с неизвестными, но равными ковариационными матрицами.

Из этих совокупностей взяты обучающие выборки объемами n₁ и n₂ соответственно:

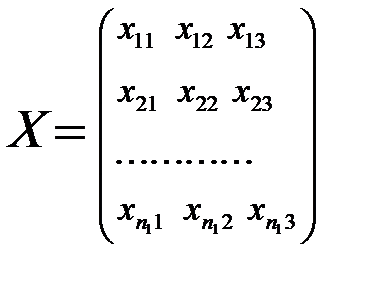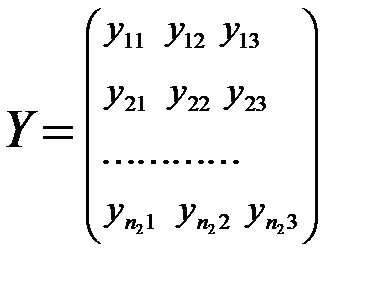; (16.1)

Целью дискриминантного анализа в этом случае является отнесение нового наблюдения (строки) из матрицы:

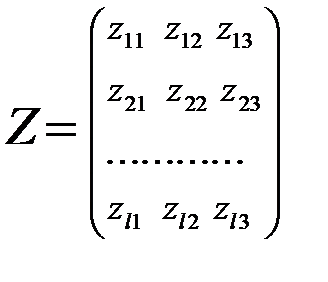(16.2)

либо к X, либо к Y.

Для решения задачи по обучающим выборкам проводятся оценки векторов средних и ковариационных матриц

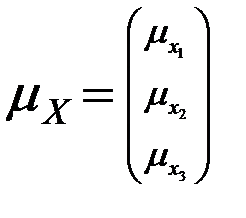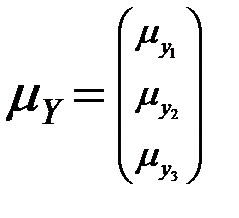; (16.3)

Затем определяется граница дискриминации – константа С.

Оценку дискриминантной функции U_i для i–й строки матрицы Z, которая характеризует i-e наблюдение, подлежащее дискриминации, получается из уравнения:

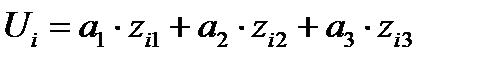(16.4)

Если U_i ≥ C, то i–e наблюдение следует отнести к совокупности X, если же U_i < C, то i–e наблюдение относится к совокупности Y.

Дискриминантный анализ допускает наличие более двух обучающих выборок, однако в этом случае задача существенно усложняется и не всегда приводит к однозначной дискриминации, т.е. не все объекты удается отнести к какому-либо классу.

Кластерный анализ

Кластерный анализ объединяет различные процедуры, используемые для проведения классификации. В результате применения этих процедур исходная совокупность объектов разделяется на кластеры или группы (классы) схожих между собой объектов. Под кластером обычно понимают группу объектов, обладающую свойством плотности (плотность объектов внутри кластера выше, чем вне его), дисперсией, отделимостью от других кластеров, формой (например, кластер может иметь очертания гиперсферы или эллипсоида), размером. Конечно, данное определение не является строгим (строгого определения не существует вообще). Если вы взглянете на географическую карту и увидите на ней горы или созвездия на звездном небе, то поймете, что такое кластеры.

Наиболее часто методы кластерного анализа используются в социологии, маркетинговых исследованиях, экономике, биологии, медицине, археологии.

Сложность задач кластерного анализа состоит в том, что реальные объекты являются многомерными, то есть описываются не одним, а несколькими параметрами (представьте, что объекты – это персональные компьютеры), и объединение объектов в группы проводится в пространстве многих измерений, что весьма нетривиально. Кроме того, данные могут носить нечисловой характер.

В целом методы кластеризации делятся на агломеративные (от слова агломерат – скопление) и итеративные дивизивные (от слова division –деление, разделение).

В агломеративных, или объединительных методах происходит последовательное объединение наиболее близких объектов в один кластер. Процесс такого последовательного объединения можно показать на графике в виде дендрограммы, или дерева объединения. Это удобное представление позволяет наглядно представить кластеризацию агломеративными алгоритмами.

Исходными данными для анализа могут быть собственно объекты и их параметры. Данные для анализа могут быть также представлены матрицей расстояний между объектами, в которой на пересечении строки с номером i и столбца с номером j записано расстояние между i-м и j-м объектом.

Если расстояния не даны сразу, то агломеративные алгоритмы начинаются с вычисления расстояний между объектами.

Переход от объектов к расстояниям между объектами – важный момент.

Расстояние между объектами – одна из мер сходства. Интуитивно понятно, что, чем меньше расстояние между объектами, тем они более схожи. Но как выбрать естественную метрику, то есть, как естественно для данной задачи измерить расстояние между объектами?

Часто используют обычную евклидову метрику, например, если объект описывается двумя параметрами, то он может быть изображен точкой на плоскости, а расстояние между объектами – это расстояние между точками, вычисленное по теореме Пифагора. Вы просто возводите в квадрат расстояния по каждой координате, суммируете их и из полученной суммы извлекаете квадратный корень. Если вы не будете возводить в квадрат покоординатные расстояния, а просто возьмете их абсолютные значения и просуммируете, то получите так называемое манхэттенское расстояние, или «расстояние городских кварталов». Такое расстояние связано с перемещением человека по улицам города, а не с движением по ровной местности.

Представьте, что вы находитесь в городе. Здесь существуют определенные правила перемещения и, соответственно, правила вычисления пройденного расстояния. Перемещаться можно только по улицам (нельзя, например, пересечь квартал или дом по диагонали). Аналогия в декартовой плоскости приводит к перемещениям только по линиям, параллельным осям координат, и, соответственно, к манхэттенскому расстоянию.