Алгоритм кластерного анализа
Кластерный анализ – это совокупность методов классификации многомерных наблюдений или объектов, основанных на определении понятия расстояния между объектами с последующим выделением из них групп, "сгустков" наблюдений (кластеров, таксонов). При этом не требуется априорной информации о распределении генеральной совокупности.
Выбор конкретного метода кластерного анализа зависит от цели классификации.
Кластерный анализ используется при исследовании структуры каких–либо совокупностей.
От матрицы исходных данных
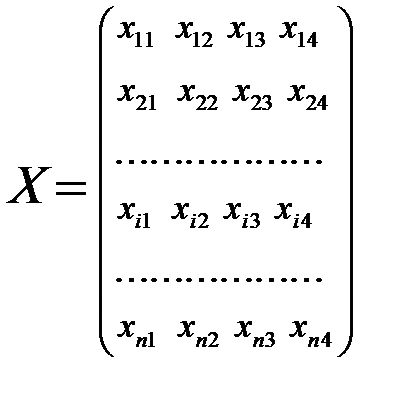 (16.5)
(16.5)
переходят к матрице нормированных значений Z с элементами:
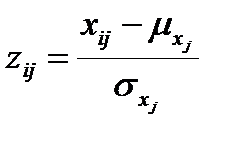 , (16.6)
, (16.6)
где:
j = 1, 2, 3, 4 – номер показателя, i = 1,2,..., n – номер наблюдения;
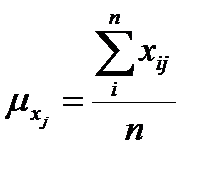 ; (16.7)
; (16.7)
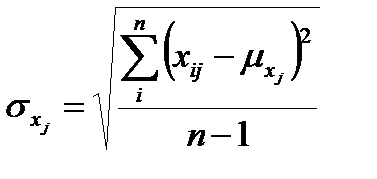 (16.8)
(16.8)
В качестве расстояния между двумя наблюдениями zi и zν используется "взвешенное" евклидово расстояние, определяемое по формуле:
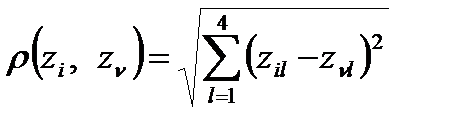 (16.9)
(16.9)
Полученные значения удобно представить в виде матрицы расстояний:
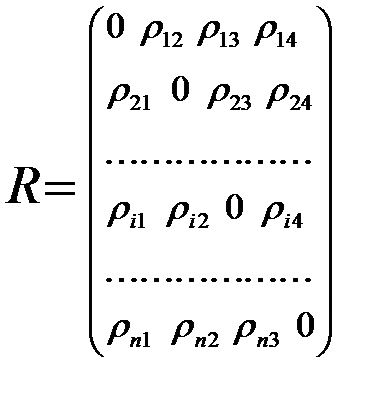 ,
,  (16.10)
(16.10)
Так как матрица R симметрическая, т.е. 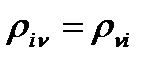 , то достаточно ограничиться записью наддиагональных элементов матрицы.
, то достаточно ограничиться записью наддиагональных элементов матрицы.
Используя матрицу расстояний, можно реализовать агломеративную иерархическую процедуру кластерного анализа. Расстояния между кластерами определяют по принципу «ближайшего соседа» или «дальнего соседа». В первом случае за расстояние между кластерами принимают расстояние между ближайшими элементами этих кластеров, а во втором – между наиболее удаленными друг от друга.
Принцип работы иерархических агломеративных процедур состоит в последовательном объединении групп элементов сначала самых близких, а затем все более отдаленных друг от друга.
На первом шаге алгоритма каждое наблюдение zi (i = 1, 2,..., n) рассматривается как отдельный кластер. В дальнейшем на каждом шаге работы алгоритма происходит объединение двух самых близких кластеров, и вновь строится матрица расстояний, размерность которой снижается на единицу. Работа алгоритма заканчивается, когда все наблюдения объединены в один класс.
Вопросы для самоконтроля
1 В чем принципиальное отличие между дискриминантным и кластерным анализами при отнесении признака к какому-то либо существующему или вновь образующемуся классу?
2 По каким критериям можно выбирать оптимальный способ классификации признака при дискриминантном анализе?
3 Чем отличаются рандомизированные и нерандомизированные решающие правила при дискриминантном анализе?
4 В чем разница между двумя общими методами дискриминантного анализа: стандартного и пошагового?
5 При каком количестве обучающих выборок дискриминантный анализ может дать достаточно достоверную оценку разделения признаков?
6 Что может служить мерой сходства между объектами в кластерном анализе?
7 Чем отличаются методы одиночной, средней и полной связей в кластерном анализе?
8 Какое количество кластеров закладывается на первом этапе классификации n объектов?
Литература
ОСНОВНАЯ
1 Лакин, Г.Ф. Биометрия / Г.Ф. Лакин - М.: «Высшая школа», 1990. – 142 с.
2 Плохинский, Н.А. Биометрия / Н.А. Плохинский - М.: «МГУ», 1970. – 368 с.
3 Свалов, Н.Н. Вариационная статистика / Н.Н. Свалов - М.: «Лесная промышленность», 1977. – 177 с.
4 Рокитский, П.Ф. Биологическая статистика: изд. 3 испр. / П.Ф. Рокитский - Минск: «Вышейшая школа», 1973. – 320 с.
5 Жученко, Ю.М. Статистическая обработка информации с применением персональных компьютеров: практическое руководство для студентов 5 курса / Ю.М Жученко – Гомель: УО ГГУ им.
Ф. Скорины, 2007.– 101 с.
6 Зайцев Г.Н. Математическая статистика в экспериментальной ботанике / Г.Н. Зайцев - М.: «Наука», 1984. –
424 с.
ДОПОЛНИТЕЛЬНАЯ
7 Мюллер, П. Таблицы по математической статистике /
П. Мюллер [и др.] - М.: «Финансы и статистика», 1982. – 64 с.
8 Павловский, З. Введение в математическую статистику /
З. Павловский - М.: «Статистика», 1967. – 285 с.
9 Карасев, А.И. Теория вероятностей и математическая статистика / А.И. Карасев - М.: «Статистика», 1979. – 279 с.
10 Бейли, Н. Математика в биологии и медицине / Н. Бейли - М.: «Мир», 1970. – 167 с.
11 Урбах, В.Ю. Статистический анализ в биологических и медицинских исследованиях / В.Ю. Урбах - М.: «Медицина», 1975. – 321 с.
12 Боровиков, В.П. Популярное введение в программу STATISTICA / В.П. Боровиков - М.: «КомпьютерПресс», 1998. – 69 с.
13 Лапач, С.Н. Статистические методы в медико-биологических исследованиях с использованием Excel / С.Н. Лапач
[и др.] - К.: «МОРИОН», 2000. – 196 с.
14 Реброва, О.Ю. Статистический анализ медицинских данных: применение пакета прикладных программ STATISTICA /
Реброва О.Ю. - М.: «МедиаСфера», 2002. – 84 с.
Приложение. Основные формулы и определения
Алгебраические преобразования
Законы действий над числами
Переместительный закон сложения: 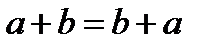 .
.
Сочетательный закон сложения: 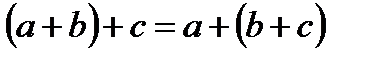 .
.
Переместительный закон умножения: 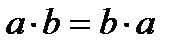 .
.
Сочетательный закон умножения: 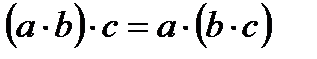 .
.
Распределительный закон умножения относительно сложения:
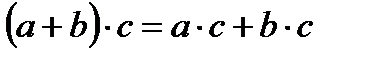
Распределительный закон умножения относительно вычитания:
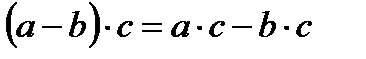
Дробные выражения
Основное свойство дроби: 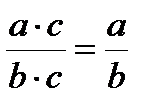 ,
, 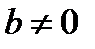 ,
, 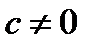
Действия с дробями (предполагается, что знаменатели дробей отличны от нуля):
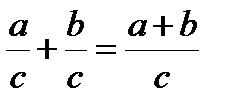 ,
, 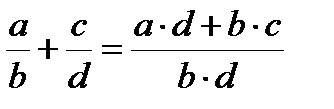
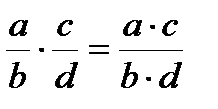 ,
, 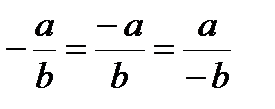
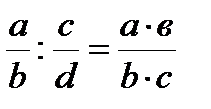 ,
, 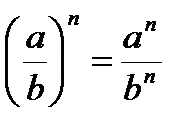
Пропорциональность
Пропорция – равенство двух отношений:
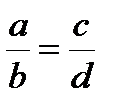 ,
, 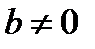 ,
, 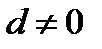
(a, d – крайние члены пропорции; b, с – средние члены пропорции).
Основное свойство пропорции: 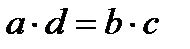 .
.
Выражение члена пропорции через остальные:
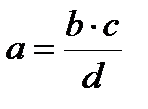 ,
, 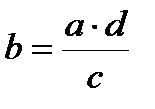 ,
, 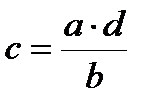 ,
, 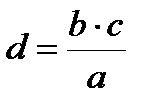 .
.
Если истинна пропорция 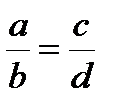 , то истинны и следующие пропорции:
, то истинны и следующие пропорции: 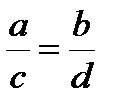 ,
, 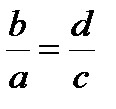 ,
, 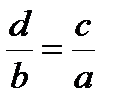 ,
, 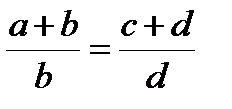 ,
, 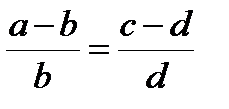 ,
, 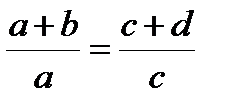 ,
, 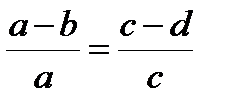 ,
, 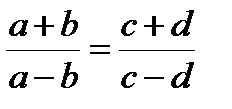 .
.
Прямая пропорциональность – функция, заданная формулой:
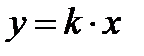 ,
, 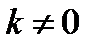
где k – коэффициент пропорциональности;
y, x – пропорциональные переменные.
Свойство прямой пропорциональности: 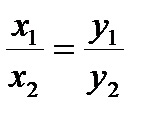 .
.
Обратная пропорциональность – функция, заданная формулой:
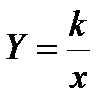 ,
, 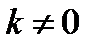 ,
, 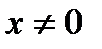
Свойство обратной пропорциональности: 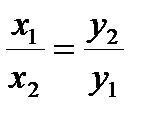 .
.
Степени и корни
Степень с целым показателем
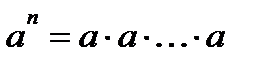 (n раз,
(n раз, 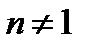 ),
), 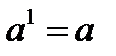 ,
, 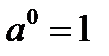
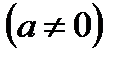 ,
, 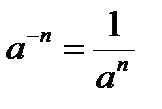
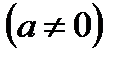 .
.
Свойства:
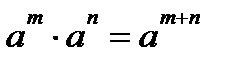 ,
, 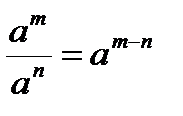 ,
, 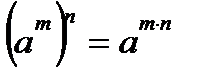 ,
, 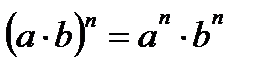 ,
, 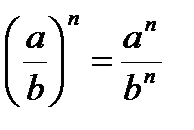 .
.
Корень n–й степени
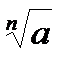 – арифметический корень n–й степени из числа а, а > 0,
– арифметический корень n–й степени из числа а, а > 0,
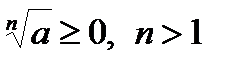 .
.
Свойства:
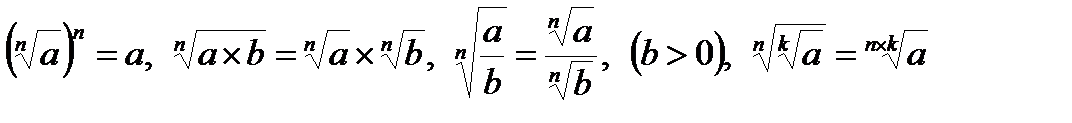 .
.
В частности, 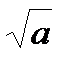 – арифметический квадратный корень:
– арифметический квадратный корень:
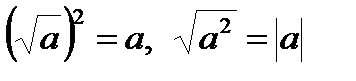 .
.
Степень с дробным (рациональным) показателем
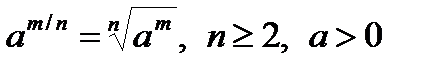 .
.
Свойства степени с действительным показателем
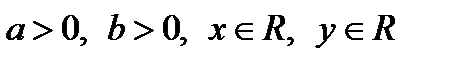
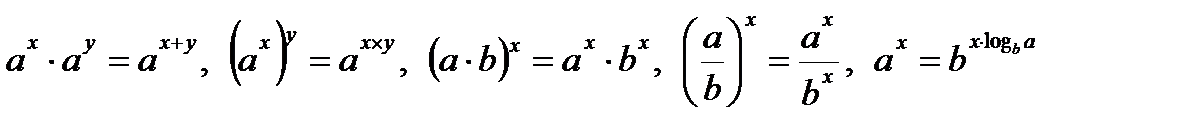 ,
,
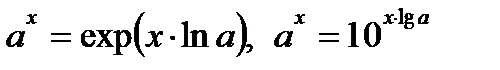
Прогрессии
Арифметическая прогрессия
Арифметическая прогрессия – числовая последовательность (an), определяемая условиями: 1) а1= а; 2) an+1 = аn + d, n = 1, 2, ...
(d – разность арифметической прогрессии).
Свойства арифметической прогрессии:
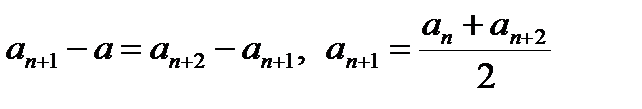
Формула n-ro члена: 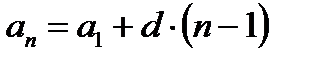 .
.
Формулы суммы n первых членов:
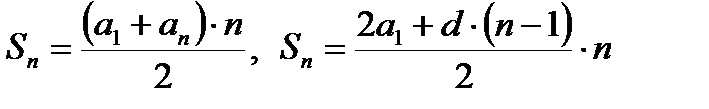
Геометрическая прогрессия
Геометрическая прогрессия – числовая последовательность (bn), определяемая условиями: 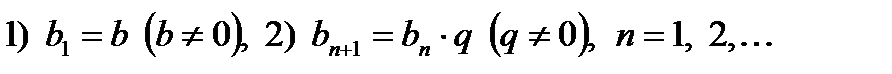
(q – знаменатель геометрической прогрессии).
Свойства геометрической прогрессии:
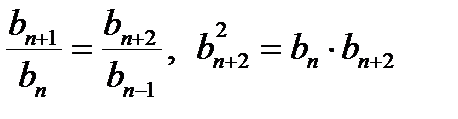 .
.
Формула n-ro члена: 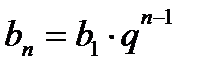 .
.
Формулы суммы n первых членов ( 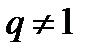 ):
):
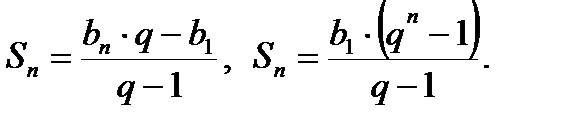
Сумма бесконечной геометрической прогрессии:
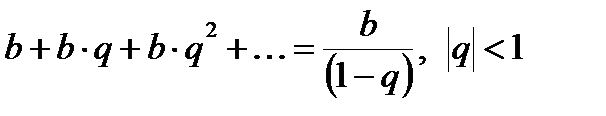 .
.
Формулы сокращенного умножения
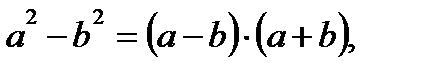
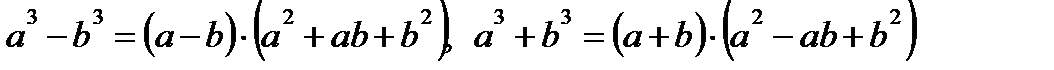
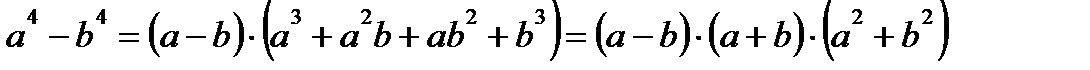
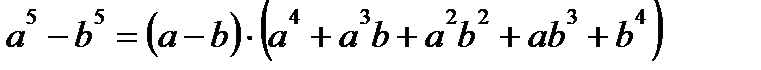
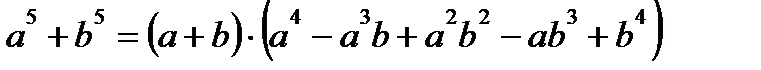
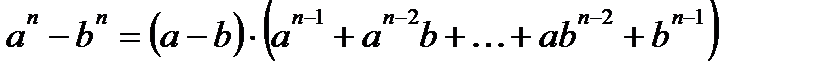
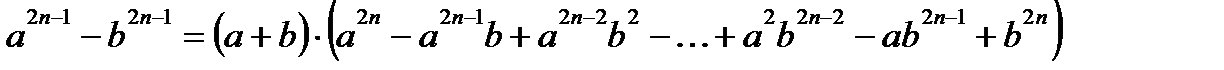
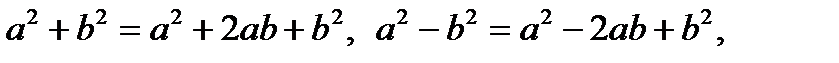
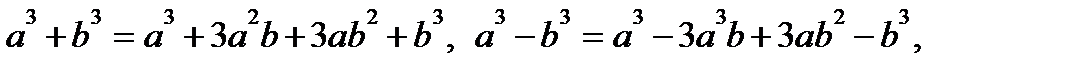
Логарифмы
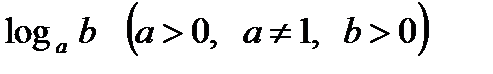 – логарифм числа b по основанию а.
– логарифм числа b по основанию а.
Основное логарифмическое тождество: 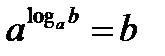 .
.
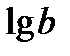 – десятичный логарифм (логарифм по основанию 10):
– десятичный логарифм (логарифм по основанию 10): 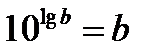 .
.
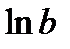 – натуральный логарифм (логарифм по основанию е):
– натуральный логарифм (логарифм по основанию е): 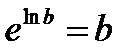 .
.
Переход от одного основания к другому:
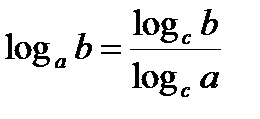
В частности,
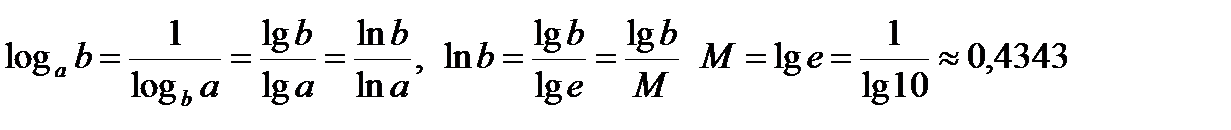
M – модуль перехода от натуральных логарифмов к десятичным.
Свойства логарифмов (u, v > 0):
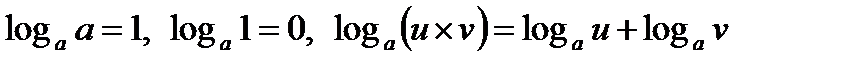
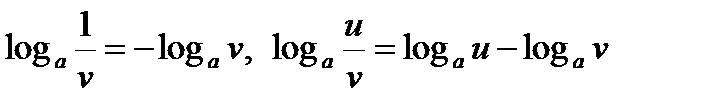 ,
,
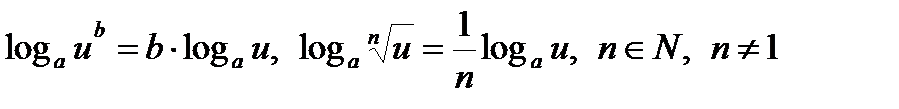 .
.
Элементы комбинаторики. Формула Ньютона
Перестановки. Размещения. Сочетания
Число перестановок из n элементов:
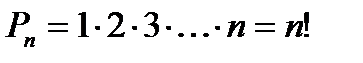 (n! – n факториал)
(n! – n факториал)
Число размещений из n по m (n ≥ m):
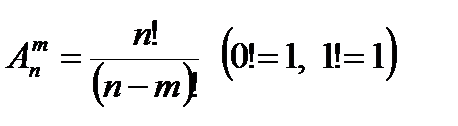
Число сочетаний из n по m (n ≥ m):
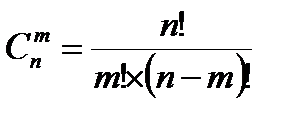
Формула бинома Ньютона
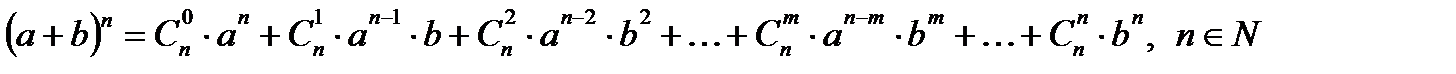
Треугольник Паскаля
Числовые функции
Основные понятия
Область определения (множество задания) функции f: 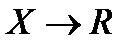 :
:
X = D(f).
Множество значений функции f:
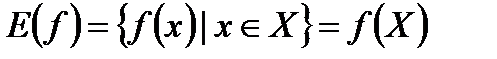 .
.
График функции:
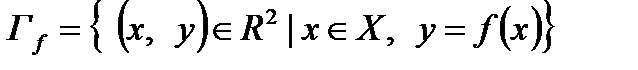 .
.
Четная функция:
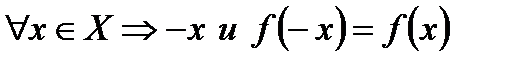 .
.
Нечетная функция:
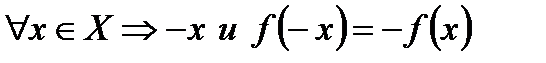 .
.
Периодическая функция (периода ω):
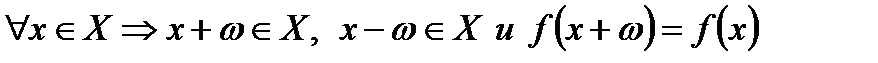 .
.
Линейная функция
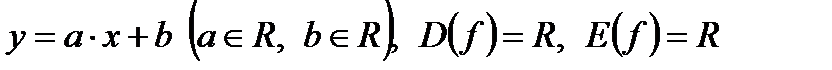
Функция строго возрастает при а > 0, строго убывает при а < 0.
График функции – прямая линия.
Квадратичная функция: 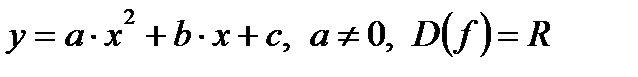
1. При а > 0 (рисунок 1–а) функция строго убывает на 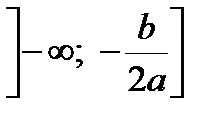 и строго возрастает на
и строго возрастает на 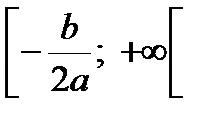 . График функции – парабола с осью
. График функции – парабола с осью 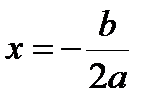 , вершиной в точке
, вершиной в точке 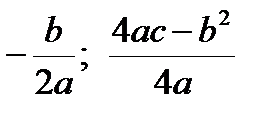 и ветвями, направленными вверх.
и ветвями, направленными вверх.
2. При а < 0(рисунок 1–б) функция строго возрастает на 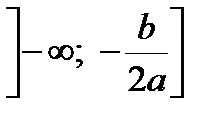 и строго убывает на
и строго убывает на 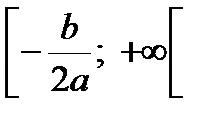 . График функции – парабола с осью
. График функции – парабола с осью 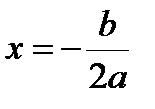 , вершиной в точке
, вершиной в точке 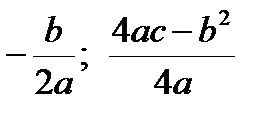 и ветвями, направленными вниз.
и ветвями, направленными вниз.
| | |
Рисунок 1 – Квадратичная функция
a) 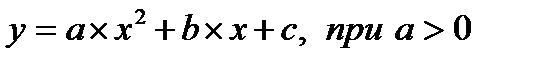 ; б) ; б) 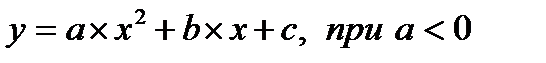
|
Степенная функция: 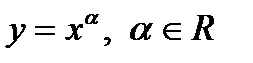
1. 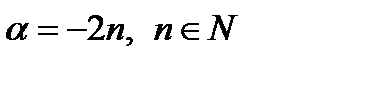 :
: 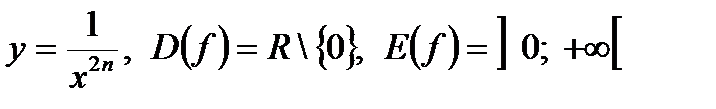 . Функция четная, строго возрастает на
. Функция четная, строго возрастает на  и строго убывает на
и строго убывает на  (рисунок 2–а).
(рисунок 2–а).
2. 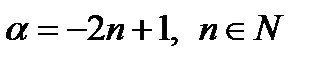 :
: 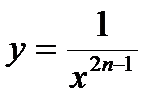 ,
, 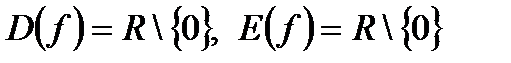 . Функция нечетная, строго убывает на
. Функция нечетная, строго убывает на 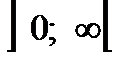 и
и 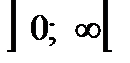 (рисунок 2–б)
(рисунок 2–б)
| | |
Рисунок 2 – Степенная функция: а) 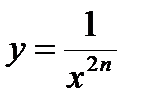 ; б) ; б) 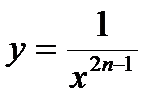
|
Экспонента: 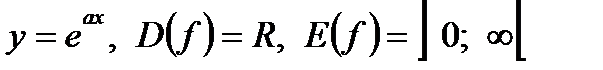 (рисунок 3–а)
(рисунок 3–а)
При a > 0 – функция строго возрастает. При a < 0 – функция строго убывает.
Показательная функция: 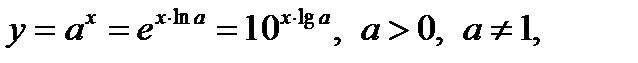
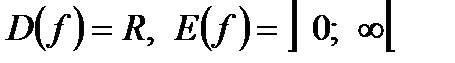 (рисунок 3–б)
(рисунок 3–б)
При 0< а< 1 функция строго убывает, при а >1 строго возрастает.
| | |
Рисунок 3 – Показательная функция: а) 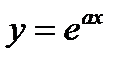 ; б) ; б) 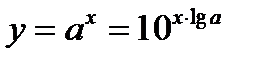
|
Логарифмическая функция
Логарифм натуральный: 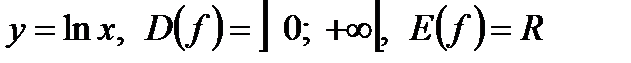 .
.
Функция строго возрастает (рисунок 4–а).
Логарифм с основанием а: 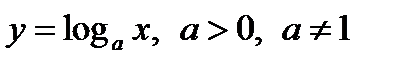 ,
,
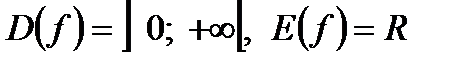
При 0 < а < 1 функция строго убывает, при а > 1 строго возрастает (рисунок 4–б).
| | |
Рисунок 4 – Логарифмическая функция: а) 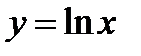 ; б) ; б) 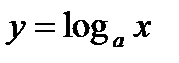
|
Логистическая функция
Уравнение Ферхюльтса: 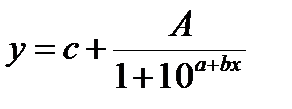 ,
, 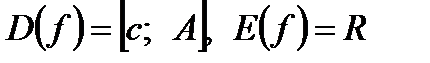
При a ≥ 0 и b ≤ 0 функция строго возрастает (рисунок 5–а).
При a ≤ 0 и b ≥ 0 функция строго убывает (рисунок 5–б).
| | |
Рисунок 5 – Логистическая функция:
а) 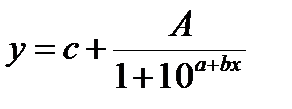 , a>0, b<0; б) , a>0, b<0; б) 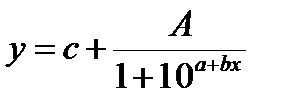 , a<0, b>0 , a<0, b>0
|
Дата добавления: 2020-10-25; просмотров: 748;











