Взвешенная средняя арифметическая

Обычно, чтобы рассчитать среднюю арифметическую, складывают все значения признака и полученную сумму делят на число вариантов. В этом случае каждое значение, входя в сумму, увеличивает ее на полную свою величину. Но не всегда это возможно. Иногда значения признака должны входить в сумму с неодинаковой поправкой. Эта поправка, выраженная определенным множителем, называется математическим весом значения.

Средняя, рассчитанная для значений признака с неодинаковыми весами, называется взвешенной средней. Взвешенная средняя арифметическая рассчитывается по следующей формуле:

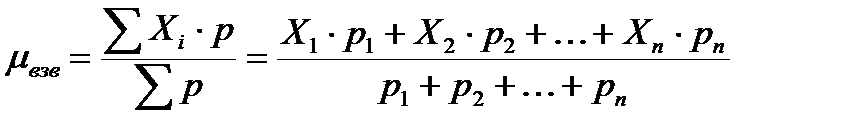, (6.4)

где:

X_i – значение признака, варианта;

p – математический вес усредняемого значения.

Чтобы рассчитать взвешенную среднюю арифметическую, необходимо каждое значение признака помножить на его вес, все эти произведения сложить и полученную сумму разделить на сумму весов.

Пример

Имеются результаты двух исследований длины хоботка пчел: в одном случае получена средняя длина хоботка 6,6 мм, в другом – 6,0 мм. Требуется получить общую среднюю, причем известно, что в первом исследовании были измерены хоботки у 100 пчел, во втором – у 20.

В данном случае значениями признака являются средние μ₁ = 6,6 и μ₂ = 6,0 мм; их весами – численности групп n₁ = 100 и n₂ = 20. Взвешенная средняя арифметическая рассчитывается следующим образом:

.

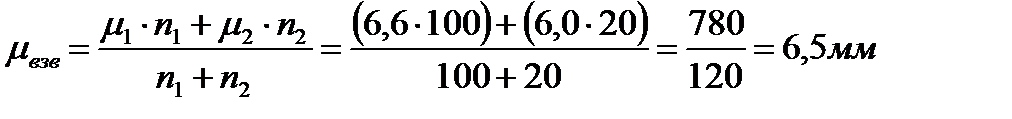Пример

В 100 кг кормовой смеси содержатся следующие количества отдельных кормов:

сена 50 кг, с содержанием белка 3%

молотой овсяной соломы 10 кг, с содержанием белка 1%

жмыха подсолнечного 20 кг, с содержанием белка 33%

отрубей пшеничных грубых 20 кг, с содержанием белка 11%

Требуется определить содержание белка в данной смеси.

Для решения этой задачи необходимо рассчитать взвешенную среднюю арифметическую. Значениями признака будет содержание белка в отдельных кормах: 3; 1; 33 и 11%, а их математическими весами — физические веса кормов, входящих в смесь: 50; 10; 20 и 20 кг. Содержание в смеси переваримого белка:

,

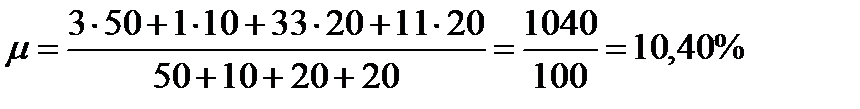т. е. в каждом килограмме смеси содержится 104 г переваримого белка.

Таким же способом рассчитываются среднее выхода продукта по нескольким партиям сырья.

Пример

Проведены три независимых наблюдения числа сокращений пульсирующей вакуоли у амебы в определенной среде. В первом наблюдении зарегистрировано 24 сокращения в 1 час, во втором – 16 и в третьем – 23, причем первое наблюдение длилось 2, второе – 6 и третье –1 час. Для определения среднего числа сокращений в час необходимо найти взвешенную среднюю арифметическую. Значениями признака будут наблюдавшиеся количества сокращений в час (24, 16 и 23), их весами – продолжительность отдельных наблюдений (2, 6 и 1 час). Следовательно,

.

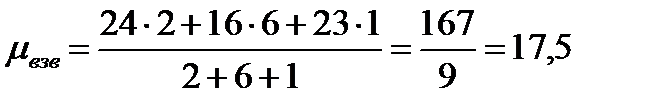Простая средняя в данном случае: 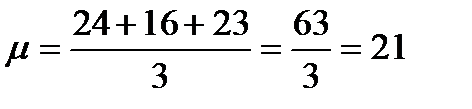даст завышенную характеристику.