Динамика объема продукции по предприятию за 1995 – 1999 гг.
| Годы | Произве-дено продук., тыс. шт. | Абсолютные приросты, тыс. шт. | Темпы роста, % | Темпы прироста % | Абсо-лют. значе-ние 1 % приро-ста, тыс. шт. | |||
| цеп. | баз. | цеп. | баз. | цеп. | ба | |||
| - | - | - | - | - | - | |||
| 0,2 | ||||||||
| 0,25 | ||||||||
| 114,3 | 14,3 | 0,35 | ||||||
| 0,40 | ||||||||
| Итог | - | - | - | - | - | - |
В нашем примере в 1996 и 1998 гг. абсолютное изменение объема продукции было одинаковым – 5 тыс. шт., но интенсивность роста объема произведенной продукции в эти годы была различной: в 1996 г. прирост в 5 тыс. ед. по сравнению с предыдущим годом составил 25 %, а в 1998 г. По сравнению с предыдущим годом – лишь 14,3 %. Аналогично один и тот же прирост в 10 тыс. ед. для 1997 и 1999 гг. означает разную интенсивность роста: в 1997 г. – прирост составил по сравнению с предыдущим годом 40 %, а в 1999г. – 25 %.
Интенсивность изменения уровней временного ряда характеризуется темпами роста и прироста.
Темп ростаесть отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные:
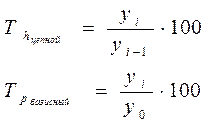
Если база сравнения по периодам меняется, то найденные темпы роста называются цепными. Если же база сравнения по периодам неизменна 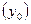 , то темпы роста называются базисными.
, то темпы роста называются базисными.
Темпы роста, выраженные в коэффициентах, принято называть коэффициентами роста:
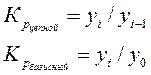 .
.
В анализе используется один из этих показателей: либо темп роста, либо коэффициент роста, ибо экономическое их содержание одно и то же, но по-разному выражено: в % 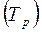 и в разах
и в разах 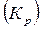 . Так, по данным таблицы можно сделать вывод, что наибольшая интенсивность роста была достигнута в 1997 г., когда темп роста составил 140 %, или в 1,4 раза превысил уровень предыдущего года.
. Так, по данным таблицы можно сделать вывод, что наибольшая интенсивность роста была достигнута в 1997 г., когда темп роста составил 140 %, или в 1,4 раза превысил уровень предыдущего года.
Если цепные темпы роста характеризуют интенсивность изменения уровней от года к году (от месяца к месяцу), то базисные темпы роста фиксируют интенсивность роста (снижения) за весь интервал времени между текущим и базисным уровнями. Так по данным табл. 10,
базисный темп роста за весь период с 1996 по 1999 г. составил 250 % (1995 г. взят за базу сравнения).
Темп приростаесть отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель):
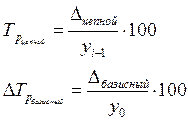
По данным табл. 10, темп прироста для 1999 г. составит: цепной – 25 % 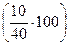 и базисный – 150 %
и базисный – 150 % 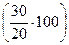 , т.е. в 1999 г. объем продукции увеличился по сравнению 1998 г. на 25 %, а в целом за весь рассматриваемый период прирост составил 150 %.
, т.е. в 1999 г. объем продукции увеличился по сравнению 1998 г. на 25 %, а в целом за весь рассматриваемый период прирост составил 150 %.
Между цепными и базисными показателями изменения уровней ряда существует следующая взаимосвязь:
а) сумма цепных абсолютных приростов равна базисному приросту (см. табл. 9, где в итоговой строке накопленный прирост за 1996 – 1999 гг. – 30 тыс. шт. – совпадает с базисным абсолютным приростом для 1999 г.);
б) произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста. Так, по данным табл. 10, имеем:
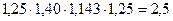 , или 250 % - базисный темп роста;
, или 250 % - базисный темп роста;
200/175=1,143, или 143,3 % - цепной коэффициент роста для 1998 г.
Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным и наоборот;
в) темп прироста связан с темпом роста: 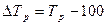 (см. табл. 10, где темпы прироста меньше темпов роста на 100). Поэтому при анализе обычно приводится какой-то один из них: темп роста, либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста. Для этого нужно от темпов прироста перейти к темпам (коэффициента) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.
(см. табл. 10, где темпы прироста меньше темпов роста на 100). Поэтому при анализе обычно приводится какой-то один из них: темп роста, либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста. Для этого нужно от темпов прироста перейти к темпам (коэффициента) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.
Так, например, изменение цен на потребительские товары и услуги за I квартал 2001 г. оказалось в Санкт-Петербурге следующим:
Изменение цен
(в % к предыдущему месяцу)
| Месяц | Январь | Февраль | Март |
| Изменение цен | 3,7 | 1,7 | 1,8 |
В целом за I квартал прирост цен составит:
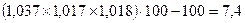 %
%
т.е. в марте 2001 г. по сравнению с декабрем 2000 г. цены выросли на
7,4 %.
Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1 % приростакак отношение абсолютного прироста уровня за интервал времени к темпу прироста за этот же промежуток времени:
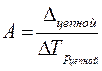 или
или
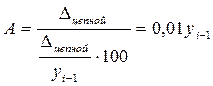
Иными словами, абсолютное значение одного процента прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде (см. табл. 10, последнюю графу). В связи с этим расчет абсолютного значения 1 % прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина – сотая часть уровня базисного периода.
Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как 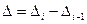 , т.е. по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости. По табл. 10 в нашем примере ускорение имело место лишь в 1997 и в 1999 гг., когда
, т.е. по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости. По табл. 10 в нашем примере ускорение имело место лишь в 1997 и в 1999 гг., когда 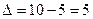 тыс. шт.
тыс. шт.
Если систематически растут цепные темпы роста, то ряд развивается с относительным ускорением. Относительное ускорениеможно определить как разность следующих друг за другом темпов роста или прироста:
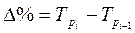 или
или 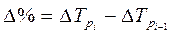
Полученная величина выражается в процентных пунктах (п.п.). По данным табл. 10, относительное ускорение имело место лишь в 1997 г. – 15 процентных пунктов по сравнению с предыдущим годом.
Относительное ускорение может быть измерено и с помощью коэффициента опережения.
Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:
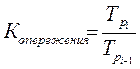
В нашем примере коэффициент опережения для 1997 г. составил: 140/125=1,12, что означает, что в 1997 г. темп роста был в 1,12 раза больше, чем в 1996 г.
Дата добавления: 2020-10-25; просмотров: 517;











