Непосредственное интегрирование
Первообразная функция и неопределенный интеграл
Функция 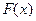 называется первообразной функцией для функции
называется первообразной функцией для функции 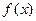 , если
, если 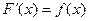 или
или 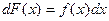 .
.
Если функция 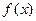 имеет первообразную
имеет первообразную 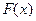 , то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении
, то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении 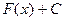 , где С – постоянная.
, где С – постоянная.
Например, для функции 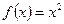 функция
функция 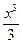 является первообразной, т.к.
является первообразной, т.к. 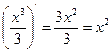 , т.е.
, т.е. 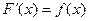 .
.
Неопределенным интеграломот функции 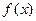 (или от выражения
(или от выражения 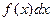 ) называется совокупность всех ее первообразных.
) называется совокупность всех ее первообразных.
Обозначение: 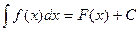 .
.
Здесь 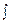 – знак интеграла,
– знак интеграла, 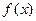 –подынтегральная функция,
–подынтегральная функция, 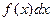 – подынтегральное выражение, х – переменная интегрирования.
– подынтегральное выражение, х – переменная интегрирования.
Отыскание неопределенного интеграла называется интегрированием функции.
Например, т.к. 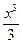 является первообразнойдля функции
является первообразнойдля функции 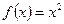 , то
, то 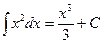 .
.
Свойства неопределенного интеграла
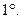
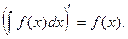
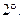
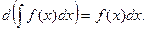
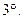
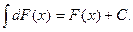
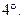
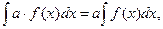 где a – постоянная.
где a – постоянная.
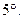
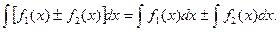
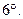 Если
Если 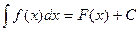 и
и 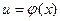 , то
, то 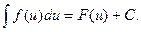
Таблица интегралов от основных элементарных функций
Перечислим интегралы от основных элементарных функций, которые в дальнейшем будем называть табличными.
I. 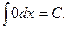
II. 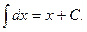
III. 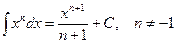
IV. 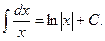
V. 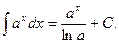
VI. 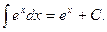
VII. 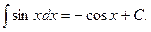
VIII. 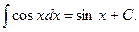
IX. 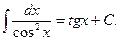
X. 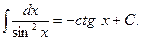
XI. 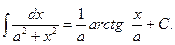
XII. 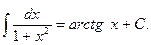
XIII. 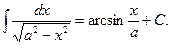
XIV. 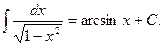
XV. 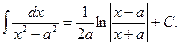
XVI. 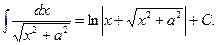
XVII. 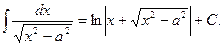
XVIII. 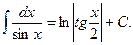
XIX. 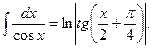
XX. 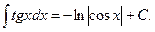
XXI. 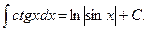
Непосредственное интегрирование
Метод непосредственного интегрирования основан на применении свойств неопределенного интеграла и таблицы интегралов.
Например, найдем интеграл
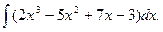
Используя свойства 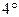 и
и 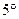 , получаем
, получаем
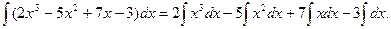
К первым трем интегралам правой части применим формулу 3, а к четвертому интегралу – формулу 2:
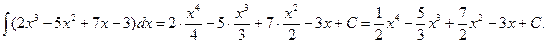
Свойство 6° позволяет значительно расширить таблицу основных интегралов с помощью интегрирования подведением под знак дифференциала.
Например, найдем интеграл 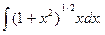
Этот интеграл можно привести к формуле 3, преобразовав его следующим образом:
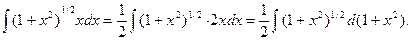
Теперь переменной интегрирования служит выражение 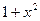 и относительно этой переменной получается интеграл от степенной функции.
и относительно этой переменной получается интеграл от степенной функции.
Следовательно,
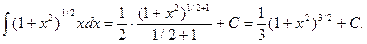
Дата добавления: 2020-10-25; просмотров: 487;











