Метод наилучшего равномерного приближения.

В этом методе параметры измерительной цепи отыскиваются из условия минимальности модуля максимума теоретической погрешности

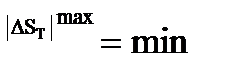
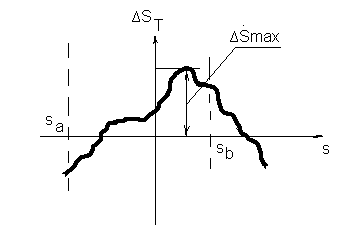
Для решения этой задачи используются специальные полиномы Чебышева, которые на заданном диапазоне аргумента наименее отклоняются от 0.

Наиболее часто используются 3 полинома:

1)

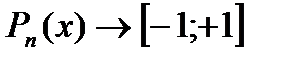
2)

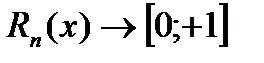
3)

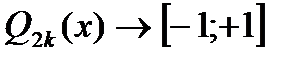
Теоретическую погрешность приравнивают к полиному и решают полученные уравнения.

11. Выявление первичных погрешностей.

Под первичной погрешностью мы понимаем любое отклонение параметров цепи от расчетных, приводящие к искажению градуировочной характеристики.

Принято все первичные погрешности разделять на две категории:

1) скалярные первичные погрешности

2) векторные первичные погрешности.

Скалярные первичные погрешности отличаются тем, что направление их действия нам заранее известно, а значение их заранее предсказать нельзя, но оно может быть принято в пределах допуска.

Векторная первичная погрешность характеризуется неопределенным и непредсказуемым направлением действия. В отличии от скалярной первичной погрешности, векторная является как бы дважды случайной: ее значение – любое в пределах допуска, а направление действия – любое в пределах зоны действия.

Методика рассмотрения первичных погрешностей механизма, предложенная академиком Н.Г.Бруевичем, позволяет строго определить возможное число первичных погрешностей каждого звена и механизма в целом.