ПОСТАНОВКА ЗАДАЧИ ИНТЕРПОЛИРОВАНИЯ
В первоначальном понимании интерполяция[4] – это нахождение промежуточных значений табличной функции («сгущение» таблицы). В более широком смысле – это восстановление функции (точное или приближенное) по известным ее значениям, то есть замена табличной функции другой, заданной в аналитическом виде. Цели интерполяции могут быть различны, но почти всегда в ее основе – желание иметь быстрый алгоритм вычисления значений f(x)для х, не содержащихся в таблице данных {xi , yi }. Компактная таблица данных и небольшая программа интерполирования могут заменить очень длинную таблицу значений функции.
При интерполяции требуется точное прохождение интерполяционной функции у=F(x) через узловые точки {xi , yi }:
F( xi ) = f( xi ) = yi . (2.4)
Исторически и прагматически наиболее важным классом интерполирующих функций является множество алгебраических полиномов (многочленов). Полиномы имеют очевидное достоинство – их значения легко вычислять. Их также легко складывать, умножать, интегрировать и дифференцировать.
Если степень полинома совпадает с количеством узлов интерполяции, то говорят о глобальной интерполяции, то есть один полином
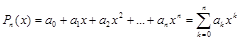
используется для интерполяции функции f(x) на всем рассматриваемом интервале изменения аргумента х.
Ясно, что потребовав, чтобы он проходил через n+1 точку , получим n+1линейное уравнение для неизвестных коэффициентов аk :
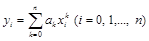 .
.
Определителем этой системы является отличный от нуля определитель Вандермонда:
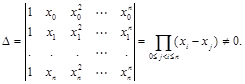
Отсюда следует существование и единственность интерполяционного полинома при xi ¹ xj .Но отметим сразу, что форм его записи может быть много.
Интерполяционные многочлены могут также строиться отдельно для разных частей рассматриваемого интервала изменения х. В этом случае говорят о кусочной (локальной) интерполяции.
Простейшим видом локальной интерполяции является линейная интерполяция (рис.2.3). Ее суть: функция считается изменяющейся между двумя соседними значениями аргумента линейно, то есть узловые точки {xk , yk}, k=0, 1,.., n соединяются прямолинейными отрезками.
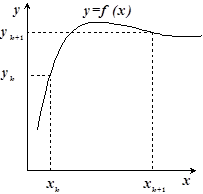 Следовательно, интерполяционный многочлен будет состоять из «кусочков» вида
Следовательно, интерполяционный многочлен будет состоять из «кусочков» вида
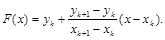
Как будет показано ниже, погрешность линейной интерполяции между узловыми точками определяется выражением
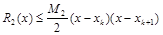 ,
,
| Рис.2.3 – Линейная интерполяция |
где 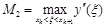 .
.
Дата добавления: 2020-10-25; просмотров: 836;











