Идентификация математических моделей

Математическое моделирование гидрологических процессов связано, как правило, с задачами идентификации. Дело в том, что традиционные методы моделирования, основанные на строгом применении общих физических законов к описанию определенных явлений, предполагает наличие измеренных параметров системы. Однако параметры подавляющего большинства исследуемых в природе объектов, например, речного бассейна, установить полностью путем измерений практически невозможно. Поэтому при математическом моделировании такие объекты обычно рассматриваются как системы с не измеряемыми параметрами. Для определения системы в этом случае используются наблюдения за факторами формирования исследуемых процессов (вход) и режимом исследуемого процесса на выходе. (рис. 1.1).

Такой подход позволяет заменить отсутствующие или ненадежные реальные физические характеристики параметрами, которые находятся по достаточно точным измеренным величинам. Эти параметры могут иметь различную физическую интерпретацию. В упрощенных моделях они обычно отражают влияние сразу нескольких факторов, и их следует рассматривать как эмпирические коэффициенты, позволяющие установить соответствие между доступными для измерения величинами.

Таким образом, недоступность непосредственных измерений ставит перед исследователями задачу косвенных определений по наблюдениям на входе и выходе исследуемой системы, что является типичной задачей идентификации.

Идентификация в широком смысле – построение оптимальной математической модели динамической системы на основании наблюдений на ее входе и выходе.

Эта задача включает в себя установление структуры математической модели, т. е. выбор общего вида уравнений и связей, и параметров этих уравнений и связей (параметризация).

Идентификация по структуре математической модели обычно основывается на совпадении граничных условий, определяющих исследуемые стороны данного явления и математическую модель. Идентификация параметров или параметризация (задача идентификации в узком смысле) проводится как правило, путем решения обратной задачи.

Задача идентификации структуры и параметров математической модели обычно ставится в следующем виде:

Задан ряд наблюдений Х за воздействием на систему и ряд У на выходе системы (рис. 2.1). Необходимо найти оператор наилучшим образом согласующий Х и У. Структура и параметры искомого оператора, как правило, неизвестны. Вместе с тем почти всегда существует информация о возможных классах структуры математической модели и возможных пределах изменений ее параметров. Источник информации — теоретические представления о механизме физических явлений данного класса. Эту информацию можно получить одним из следующих способов: просмотр литературы, составление библиографических справок, анализ источников информации и данных наблюдений, анализ экспериментальных данных, консультации со специалистами и экспертами и т. д. Также одним из возможных источников информации могут быть априорные предположения, включенные в процесс моделирования и основанные, как и предыдущие источники информации, на имеющемся уже опыте.

В тех случаях, когда имеющейся информации недостаточно для построения модели, выдвигаются рабочие гипотезы, принимаются различные допущения, которые в сумме представляют собой априорное математическое описание процессов исследуемой системы. При получении новой информации в процессе идентификации или работы модели се структура и параметры могут быть пересмотрены.

Математическая модель становится адекватной, то есть вполне соответствующей, и приобретает объективное содержание только при выполнении следующих условий.

- Во-первых, представления, составляющие априорное содержание модели, должны быть связаны определенными соотношениями с объективными характеристиками изучаемого объекта.

- Во-вторых, должна быть разработана и использована четкая процедура проверки справедливости системы умозаключений, следующих из данной математической модели. Этим гарантируется получение объективных результатов, не зависящих от произвольных желаний ис­следователя.

- В-третьих, должна быть обеспечена определенная степень согласованности между результатами, полученными при экспериментировании с объектами, и соответствующими значениями, вычисленными или «снятыми» с модели.

- В-четвертых, должно быть определенное соответствие между предсказаниями на основе математической модели и реальным поведением объекта.

Следует отметить, что определение параметров модели путем непосредственного решения уравнений, связывающих наблюдения на ее входе и выходе, может привести к большим погрешностям, так как небольшие изменения входных и выходных данных могут значительно изменить определяемые таким образом параметры. Поэтому в некоторых случаях при определении параметров математической модели [31] привлекают теорию некорректных задач, позволяющую с помощью дополнительной информации получить более устойчивые решения с точностью, соответствующей точности задания исходных данных и адекватности математической модели реальному процессу [56].

Нередко при определении параметров рассматриваемой системы отсутствует гарантия, что будут получены фактические значения параметров. Это объясняется тем, что в значениях исходных данных могут быть большие погрешности, вызванные, с одной стороны, погрешностями наблюдений, с другой — выборочным характером исходных данных. Роль отдельных грубых погрешностей можно в значительной степени снизить, объединив все имеющиеся наблюдения и дополнительную информацию о параметрах. Однако при объединении наблюдений число уравнений превышает количество искомых параметров, причем используются неточные, а иногда противоречивые соотношения. В этом случае постановку задачи меняют, ищут не точные значения параметров, а их оптимальные значения в соответствии с заранее выбранными условиями.

2.4. Методы оптимизации

В более общей постановке задачу определения оптимальных параметров можно рассматривать как задачу отыскания таких значений параметров, при которых некоторая заданная функция, зависящая от сходимости рассчитанных значений и данных наблюдений, достигает минимума. Такая функция называется критерием оптимизации или критерием качества.

Критерий качества – ­ некоторая заданная функция, зависящая от сходимости рассчитанных значений и данных наблюдений,

В отличие отметодов определения параметров, основанных на непосредственном решении уравнений относительно этих параметров и дающих вполне определенный набор решений для рассматриваемых входных и выходных данных, методы оптимизации могут давать различные значения параметров в зависимости от принятого критерия качества. Большим достоинством метода оптимизации является возможность охватить практически неограниченный объем наблюдений и дополнительную априорную информацию, ограничивающую область, в которой должны искать решение. Это позволяет при достаточном объеме информации находить значения параметров, близкие к фактическим.

Вследствие универсальности метода идентификации на основе оптимизации требуется, чтобы поставленная задача была достаточно обоснована физически, а также, чтобы была уверенность в существовании семейства сравнительно мало отличающихся решений. Без этого применение методов оптимизации создаст лишь иллюзию решения задачи идентификации параметров, а сами параметры, при которых получают хорошую сходимость поверочных расчетов, при испытаниях на независимом материале дают резуль­таты, совершенно отличающиеся от фактических.

Важную роль при оптимизации играет выбор критерия качества, от которого, как отмечалось, во многом зависят конечные результаты расчетов.

Строгое физическое обоснование имеют критерии, характеризующие отклонения фактических значений от расчетных:

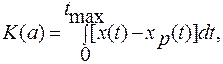(2.3)

где x(t) и х_р(t) — соответственно фактические и рассчитанные значения X.

Однако результаты оптимизации на основе этого критерия могут иметь неопределенный характер, если распределение разности x(t) - x_p(t) является симметричным.

В последнее время в различных расчетах за критерий качества часто принимается абсолютная погрешность расчетов

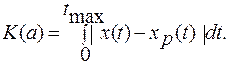(2.4)

Этот критерий дает более определенные результаты. Однако использовать его в расчетных формулах в некоторых случаях достаточно сложно.

Наиболее часто критерий качества представляется в виде среднего квадрата или суммы квадратов разностей фактических и рассчитанных значений

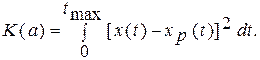(2.5)

Именно на этом критерии основывается принцип наименьших квадратов, широко используемый (см. ниже) в различного рода выводах.

Для придания большего веса высоким значениям исходной величины иногда используется критерий вида

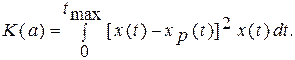(2.6)

В некоторых работах используются нормированные критерии качества, например

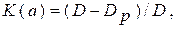(2.7)

где D и D_p — соответственно дисперсия исходного и рассчитанного ряда.

В заключение следует отметить, что проблема выбора критерия качества для оптимизации параметров моделей стока тесно связана с проблемой объективной оценки точности расчета исследуе­мой величины. Например, если оценку точности расчета гидрографа паводка произвести по точности расчета отдельных ординат, то небольшие сдвиги фаз могут дать большие погрешности, и рассматриваемая методика окажется непригодной, несмотря на то, что в общем она дает верное представление о форме гидрографа.

На первых этапах развития геоэкологических исследований, когда структуры математических моделей были очень просты и включали, как правило, не более 2—5 параметров, оптимизацион­ные расчеты заключались в последовательном переборе всех возможных значений параметров и выборе тех из них, которые дают минимальное значение критерия качества. Этот простой и надежный метод поиска экстремума критерия качества называется сканированием.

Сканирование ­– последовательный перебор всех возможных значений параметров и выбор тех из них, которые дают минимальное значение критерия качества.

Сканирование относится к методам пассивного поиска, т. е. к тем методам, при которых направление последующего поиска не зависит от результатов предшествующих шагов поиска. Преимущество сканирования состоит в том, что оно позволяет находить истинный минимум критерия качества при любой зависимости (топографии) критерия качества от значений параметров. Однако сканирование возможно не во всех случаях, а только тогда, когда число параметров и их значений невелико.

Большое распространение в технических приложениях получил метод покоординатного спуска (метод Гаусса — Зейделя). Этот метод состоит в минимизации критерия качества для каждого из параметров при постоянном значении остальных параметров, причем последовательность оптимизации каждого параметра устанавливается в зависимости от его влияния на функцию качества. Значение параметра, дающее минимум критерия качества, использу­ется затем для оптимизации следующего параметра и так до тех пор, пока наблюдается заметное уменьшение критерия качества.

Метод покоординатного спуска дает хорошие результаты при сравнительно простой топографии критерия качества. Например [20], на рис. 2.2 представлены разные топографии критерия качества при двух параметрах а₁ и а_2. В соответствии с алгоритмом названного метода, принимаем начальное значение а₂ на левом графике рисункаравным нулю, и изменяем а₁, вдоль оси абсцисс от начального значения до тех пор, пока будет наблюдаться уменьшение критерия качества (точка b);за­тем изменяем а₂ вдоль оси ординат от точки b до тех пор, пока наблюдается уменьшение

Исправить номер рисунка

критерия качества (точка с), затем снова изменяем а₁ и т. д. В случае, представленном на левом графике рис. 2.2 а, критерий качества быстро достигает минимума. Гораздо сложнее обстоит дело_: когда критерий качества имеет более чем один минимум, или если его топография имеет направление, вдоль которого критерий качества меняется намного медленнее, чем в других направлениях (см. рис. 2.2 б), — овражный тип топографии. В этом случае эффективность метода покоординатного спуска резко снижается. Из рис. 2.2 б видно, что продвижение к минимуму здесь прекратится задолго до достижения самого мини­мума.

Для ускорения движения к минимуму используется анализ топографии критерия качества в окрестностях какой-либо точки. Этот анализ заключается обычно в расчете тех или иных градиентов. Подробное изложение этих методов дается в работе [55].