Общие понятия о математических моделях

Математические модели геоэкологических процессов

Понятие «математические модели» является в настоящее время непременным атрибутом большинства исследований, в том числе и чисто теоретических. В последние годы расширилось и само понятие моделей. Когда то раньше модель это непременно какая-то материально реализованная система, имеющая черты внешнего сходства с рассматриваемым объектом. В настоящее время:

Модель — каким-либо образом реализованная система, которая способна замещать исследуемый объект так, что ее изучение даст новую информацию об этом объекте.

Моделирование – процесс построения (или выбора) и изучения моделей в целях получения новых знаний об исследуемом объекте

В общем случае модель может быть нематериальной и не иметь никакого внешнего сходства с исследуемым объектом.

Предметная модель - материальный объект, отражающий свойства исследуемого объекта и способный его замещать в процессе эксперимента.

Мысленная модель –мысленный образ, способный замещать исследуемый объект так, что его изучение дает новую информацию об этом объекте.

Предметное моделирование применяется тогда, когда необходимо выяснить не общие физические закономерности, а детально изучить вполне конкретный процесс, происходящий на исследуемом объекте с определенными геометрическими и физическими свойствами при заданных режимных условиях, проводить же эксперименты с самим этим процессом либо совсем не удается, либо они крайне затруднены.

Среди предметных моделей обычно выделяют пространственно-временные (геометрические), физические и предметно-математические модели.

Физические и пространственно-временные модели сходны с оригиналом по физической природе, геометрической форме или характеру изменения во времени. Примеры таких моделей: уменьшенные копии ГЭС, уменьшенные копии участка реки, копии прибора

Предметно-математические модели конструируются из элементов иной, чем исследуемый объект, физической природы, но описываются теми же математическими зависимостями. Они имеют ряд преимуществ по сравнению с физическими и пространственно-временными моделями: более универсальны; переход от задачи к задаче не требует каждый раз построения новой модели; изменение параметров моделируемой системы, как правило, не вызывает больших переделок модели; сами модели относительно просты и дешевы.

Предметно-математические модели могут строиться на основе прямой аналогии между величинами, присущими физически различным явлениям.

Так, в исследованиях речного стока в 60—70-х годах был рас­пространен расчет гидрографов стока на электронных моделирующих установках, основанный на использовании аналогии между генетической формулой стока и формулой изменения силы тока i на выходе электри­ческой системы из RС-элементов в зависимости от изменения вход­ного напряжения U.

Действительно, первая из них имеет вид:

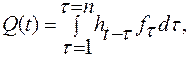(2.1)

где Q — расход воды в замыкающем створе водосбора, h—слой дождевых осадков минус потери, f — распределение единичных площадей стекания, п — число единичных площадей, t — время, τ— время добегания.

Вторая

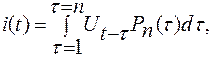(2.2)

где Р_n — весовая функция системы, представляющая собой реак­цию устройства на единичный импульс, поданный на его вход.

Решающий блок таких систем — это электрическая цепь из п последовательно соединенных RС-элементов, состоящих из актив­ного сопротивления R и емкости С.

Мысленные модели конструируются с помощью языка знаков (математические формулы и другие обозначения), рисунков, схем и прочих материальных средств. Однако все преобразования в них, все переходы в другие состояния осуществляются мысленно, т. е. в сознании человека.

Из класса мысленных моделей для исследователей особый интерес представляют математические модели.

Математическая модель – совокупность математических и логических соотношений, с помощью которых устанавливаются количественные и качественные характеристики изучаемого явления и его связей с окружающей средой.

Широкое распространение математических моделей в науках о Земле объясняется следующими обстоятельствами:

1. Для решения задач, связанных с природными явлениями, необходимо использовать те или иные математические методы. Выбор этих методов нередко сам по себе представляет достаточно сложную задачу, решение которой далеко не всегда является бесспорным. Между тем от того, какой математический метод будет использован, в большой степени зависит конечный результат исследований, особенно в сложных условиях геоэкологического анализа. Эта зависимость с течением времени все больше возрастает.

Во многих отношениях задача выбора математического метода упрощается тем, что современная математика представляет собой колоссальный арсенал математических структур, заготовленных впрок. Каждую из этих структур можно использовать при выполнении определенных граничных условий. Если исследуемый процесс или явление соответствует этим условиям, то математическая структура может выступать в качестве полномочного представителя процесса или, иначе говоря, служить его математической моделью.

2. Если рассматриваемый процесс адекватно описывается какой-то математической моделью, то это означает, что для его описания (характеристики) можно использовать весь круг понятий, связанных с данной математической моделью. Этот круг понятий представляет собой дополнительную информацию, которая часто является весьма весомым вкладом в общие знания о рассматриваемом явлении или процессе. Например, решение о том, что для описания данного ряда наблюдений может использоваться математическая модель в виде последовательности не связанных между собой значений случайной величины, часто означает, что для полной характеристики этого ряда достаточно знать вид одномерного закона распределения и три числовые характеристики: математическое ожидание, среднее квадратическое отклонение и коэффициент асимметрии. Иногда используется четвертая характеристика - эксцесс.

3. Во многих случаях математическая модель может замещать исследуемый объект, служить его полномочным представителем во всякого рода испытаниях. Так, часто невыполнимые на практике опыты с объектами природы или эксперименты с ними могут быть заменены численными экспериментами с математическими моделями.

Таким образом, использование математических моделей облегчает выбор и использование математического аппарата, представляет в распоряжение исследователя дополнительную информацию о рассматриваемом процессе или явлении, а также позволяет произвести эксперименты в тех случаях, когда на объектах природы они невозможны или затруднены в силу тех или иных обстоятельств.

В основе математического моделирования лежат явления изоморфизма и гомоморфизма.

Изоморфными называются такие две системы А и В с заданными в них отношениями, для которых выполняются следующие условия:

– каждому объекту а из системы А однозначно соответствует

объект B из системы В и наоборот;

– каждому отношению в системе А однозначно соответствует отношение в системе В и наоборот;

– если некоторые объекты системы А (а1, а2,…) связаны отношением R, то соответствующие объекты системы В (b1, b2…) должны быть связаны отношением R и наоборот.

Изоморфное отображение какого-либо объекта является адекватным или тождественным.

Гомоморфными называются такие две системы А и В,между объектами которых нет взаимооднозначного соответствия, т. е. одна система является лишь упрощенной копией другой.

Гомоморфизм указывает на единство, связь, взаимодействие и взаимозаменяемость в определенных пределах различных явлений, на сходство их формы и отдельных закономерностей. Поэтому в строго определенных границах и условиях (граничные условия) можно заменить изучение одного явления изучением другого, подобного ему по структуре.

При исследовании природных явлений, вследствие сложности рассматриваемых процессов, математические модели являются чаще всего гомоморфным образом объекта.