Общее обоснование применений статистических методов в геоэкологии

Многие процессы, происходящие в окружающей среде, являются ин­тегральными характеристиками или результатом взаимодействия многих геофизических процессов на сравнительно больших терри­ториях (прямая и рассеянная радиация, осадки, температура воз­духа и подстилающей поверхности, давление и влажность воздуха, скорость и направление ветра и т. д.), физико-географических условий бассейна (ландшафт, почвы, геологичское строение, рас­тительность и т. д.), хозяйственной деятельности человека и т. д.

Исходя из этого, можно записать, что

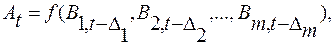(2.9)

где А — рассматриваемое явление, т — число его причин, В_j (j = 1, 2, ..., т)— причины или комплексы причин, ∆_j — запаздывание воздействия причин.

Если бы все факторы, характер их влияния на процесс А и взаимодействия между собой были известны и однозначны, то для решения уравнения (2.9) могли бы быть использованы методы классической математики, в частности, аппарат дифференциальных уравнений, и на их основе получены точные представления о процессе А в настоящем, будущем и прошлом.

Однако практически ни в одной задаче прикладных и теоретических исследований получить однозначное решение уравнения (2.9)не удалось. Попытки повышения точности решения за счет учета новых факторов, установления новых причинно-следственных связей и т. д. все чаще оказываются безрезультатными. Собственно именно это обстоятельство привело к широкому распространению методов теории вероятностей и математической статистики в науках о Земле. Практически все исследователи, работающие в этой области в настоящее время, признают необходимость применения статистических методов. Однако о характере их использования существуют различные точки зрения. В соответствии с одной из них статистические методы в науках о Земле есть временное средство, вызванное многофакторностью гидрометеорологических и других процессов и недостаточной изученностью многих из них. В соответствии с другой точкой зрения статистические закономерности объективно отражают природу рассматриваемых процессов и, следовательно, аппарат математической статистики является наиболее подходящим для их описания.

Рассмотрим более детально эти точки зрения. Если проанализировать, например, факторы, определяющие состояние окружающей среды, то, во-первых, окажется, что этих факторов очень много и конкретное их число определить практически невозможно; во-вторых, более или менее точный учет большинства из этих факторов является пока, а возможно и в бу­дущем, неразрешимой проблемой; при этом точность учета многих факторов (осадки, средняя влажность, почвы в бассейне и т. д.) нередко уступает точности непосредственных измерений самого исследуемого процесса; и, в-третьих, о законах взаимодействия этих факторов и характере их изменения во времени часто известно также мало или даже меньше, чем об изучаемой интегральной характеристике.

Исходя из этого анализа формулу (2.9) следует переписать в виде

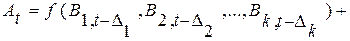
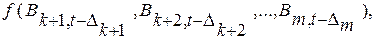(2.10)

где k — число известных, определенных факторов; 1, 2, …,к ­ –номера известных факторов; k + 1, k + 2, ..., m — номера неопределенных факторов, которые не могут быть учтены при описании процесса А.

Именно такое представление о формировании процесса А послужило для многих исследователей обоснованием использования статистических методов в науках о Земле.

Вместе с тем приведенное обоснование вызвало несколько односторонний взгляд на статистические методы как на необходимое, но временное средство. Действительно, необходимость использования статистических методов здесь объясняется только недостаточной на данном этапе изученностью процессов формирования стока. Исходя из этой точки зрения с повышением степени изученности область применения статистических методов будет постепенно сокращаться и в конце концов сойдет на нет.

Однако приведенные соображения совершенно не учитывают ряд обстоятельств, в частности появления элементов случайностей, сопровождающих весь процесс формирования природных процессов.

Если исходить из понятий классической физики, рассматриваю­щей окружающий мир как совокупность отдельных частей, взаимодействующих по однозначным динамическим законам, то появле­ние элементов случайностей невозможно. В мире классической фи­зики представляется, что все связи имеют однозначный характер, и развитие процессов происходит по строгим динамическим законам. Отсюда для полного определения того или иного процесса достаточно установить только эти связи и законы. Однако в современной физике произошли коренные изменения взглядов на окру­жающий мир. Так, в частности, возникло представление о том, что «. . .части не являются отдельными независимыми образованиями и ни один объект не может быть индивидуализирован» [36]. Отсюда:

«Представление о том, что материю возможно представить в виде совокупности отдельных независимых частей. . . заменяется представлением о том, что Вселенная является неделимым целым, отдельные части которого имеют смысл абстракций или приближений, справедливым лишь в классическом пределе» [36].

Интересно, что этот принцип был сформулирован еще Аристотелем в труде «Метафизика», в котором он отмечал, что «Целое является чем-то большим, нежели сумма его частей».

Сейчас, пожалуй, повсеместное признание получили свойства эмерджентности сложных систем

Эмерджентность – наличие у данной системы некоторых особых свойств, не присущих ее элементам: блокам и подсистемам, и даже не присущих их сумме.

Таким образом, свойства больших систем, с которыми мы несомненно и в географии и в геоэкологии имеем дело, невозможно свести к сумме свойств их компонентов.

Признание окружающего мира «неделимым целым» и понимание конкретных объектов и процессов природы как некоторой более или менее оправданной абстракции объясняет появление элементов случайностей, а следовательно, и принципиально веро­ятностный характер поведения объектов, их вероятностную при­роду.

Необходимо также отметить, что формирование природных процессов является, как правило, многоступенчатым, т. е. непосредственные причины любого явления в свою очередь имеют свои причины, вплоть до гипотетических абсолютных первопричин (профакторов), находящихся на формально бесконечно удаленной степени формирования. Даже если принять что каждая причина данного процесса в свою очередь имеет не больше двух причин то, и в этом случае имеем геометрическую прогрессию числа причин от ступени к ступени вплоть до очень большого числа начальных профак­торов (рис. 2.3). При этом в процессе взаимо­действия причин возника­ют недетерминированные перекрещивания причин­но-следственных цепей, приводящие к возникно­вению неконтролируемых элементов случайностей ЭС [5].

Исправить подпись к рис.

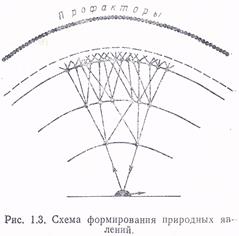
Возникая на всех ступенях формирования и передаваясь в цепном процессе воздействий со ступени на ступень, ЭС входят, в конце концов, в массовом количестве в рассматриваемое явление. Таким образом, любая элементарная связь природных процессов уже неоднозначна, она включает в себя элементы случайностей, по­тому что сама по себе не наблюдается в природе, а является лишь, абстракцией, используемой нами в тех или иных целях. Исходя из этого связь сложного процесса, являющегося по своему происхож­дению многофакторным и многоступенчатым, с причинами может быть представлена в виде

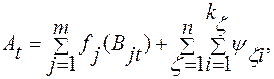(2.11)

где в данном случае п — число промежуточных ступеней формиро­вания между явлением и рассматриваемыми причинами; т — число причин; k_ζ— число элементов случайностей на каждой ζ -й ступени формирования; ψ_ζi— элементы случайности, появляю­щиеся на ζ -й ступени при взаимодействии причин [5].

При этом чем больше этих причин и большее число промежу­точных ступеней имеет процесс формирования, тем больше эле­ментов случайностей включается в данный процесс. Отсюда, на­пример, при n→∞ и соответственно при m→∞ получим , что

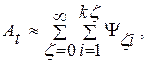(2.12)

т. е. что процесс А почти полностью определяется массой элемен­тов случайностей¹, влияние же причин, лежащих в основе формирования этого процесса, почти или совсем не про­является.

Таким образом, вследствие вероятностной природы колебаний стока и вероятностного характера воздействий окружающей среды, причинно-следственные связи колебаний факторов окружающей среды также должны быть вероятностными. Из приведенных соображений следуют два важ­ных вывода. Во-первых, несмотря на то, что любой процесс формируется вполне определенными причинами и посредством вполне определенных причинно-следственных связей, в некоторых случаях, когда рассматриваются отдаленные причины, связь его с этими причинами из-за многоступенчатости и много­факторности формирования гидрологических процессов, а также проявления элементов случайностей может стать исчезающе малой и в конечном итоге определение влияния конкретной причины 'на развитие процесса - может стать невозможным. Во-вторых, даже если бы мы знали все или, более правильно, все основные причины формирования природных макропроцессов, имеющейся полной информации все равно было бы недостаточно для полного динами­ческого описания макропроцессов.

Общая неопределенность исследуемого процесса по отношению к внешним и внутренним причинам (в дальнейшем, для краткости, случайность) может быть выражена через критерий случайно­сти δ

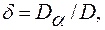(2.13)

где D и D_a — соответственно дисперсии ряда значений А и его случайной составляющей, вызванной воздействием элементов слу­чайности.

При δ=0 влияние внешних и внутренних причин полностью определяет процесс А. Вследствие вероятностной природы и вероятностного характера причинно-следственных связей процессов природы такая ситуация принципиально невозможна. При δ=1 влияние внешних и внутренних причин не проявляется, раз­витие процесса полностью определяется элементами случайности. Прогнозирование такого процесса на основе учета этих причин принципиально невозможно. Очевидно, что весь континуум природных процессов по случай­ности находится между этими крайними значениями δ. Здесь интересный парадокс: с одной стороны, если убрать причины формировании процесса, то он не появиться, с другой стороны эти причины не влияют на изменения процесса

Следует отметить, что опытное значение критерия случайности процесса δ, определяемое по отношению к внутренним и внешним причинам, всегда больше действительного значения. Это объясняется неполнотой и несовершенством научных знаний, не учетом всех действующих факторов и т. д. Очевидно, что с раз­витием научных исследований значение δ, полученное в результате опыта, должно стремиться к действительному значению.

Таким образом, из проведенного анализа следует, что природа гидрологических процессов, характер причинно-следственных свя­зей и законов, управляющих ими, являются вероятностными. Именно поэтому обычные для классической теории анализа методы математических исследований, основанные на предположении о динамическом поведении объектов, оказались бессильными для анализа многих гидрологических процессов. Так, например, не привело и не могло привести к серьезным результатам использова­ние аппарата дифференциальных уравнений, связанного с класси­ческой физикой. Действительно, если ни характер изменений во времени, ни закон взаимодействия отдельных факторов не изучены и вряд ли могут быть изучены вообще в классическом измерении па основе однозначных причинно-следственных связей, то приме­нение аппарата дифференциальных уравнений, по выражению Б. В. Гнеденко [14], носит элементы грубого произвола.

Очень часто в различного рода исследованиях противопо­ставляются статистические и физические (генетические) методы. При этом указывается, что во всех науках естествознания обще­принятыми являются физические методы и только в гидроло­гии отдается предпочтение статистическим методам исследований. По этому поводу следует отметить, что противопоставление ста­тистических и физических методов исследования было в какой-то степени оправдано до середины 30-х годов. Однако с тех пор про­изошел коренной пересмотр отношения к использованию статисти­ческого аппарата во многих науках естествознания, в том числе в физике и генетике, связанный с пересмотром соотношений стати­стических и динамических закономерностей в природе. Если раньше назвать метод исследований физическим означало, что в основе его лежит использование динамической модели в виде той или иной функциональной зависимости, то сейчас это было бы неверно. Например, крупнейший физик нашего времени М. Борн в книге «Физика в жизни моего поколения» отмечает: «Статисти­ческие методы в физике по мере развития науки распространялись, все больше и больше, и сегодня можно сказать, что современная физика полностью опирается на статистическую основу. . . Это яв­ляется событием в истории человеческого мышления, значение ко­торого выходит за рамки самой науки».

Литература

31. Кучмент Л.С.Математическое моделирование речного стока .–Л.:Гидрометеоиздат, 1972.–190 с.

56.Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986

14. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1969. 400 с.

70. Шитиков В.К. Розенберг Г.С., Зинченко Т.Д. Количественная гидроэкология: методы, критерии, решения. Кн.281 – М.: Наука, 2005. – 281 с.

36. Мякишев Т.Я. Динамические и статистические закономерности в физике.М.: Наука, 1973. 272 с.