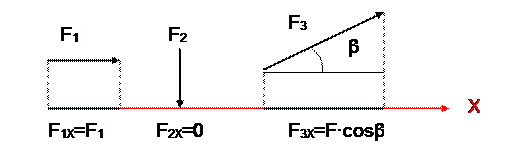
Проекция силы на две взаимно перпендикулярные оси.
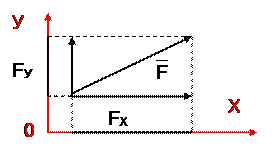
| Формула для определения модуля силы через её проекции на оси координат
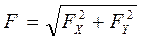
|
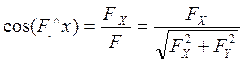 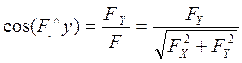
|
Пример:
Проекция векторной суммы сил на ось
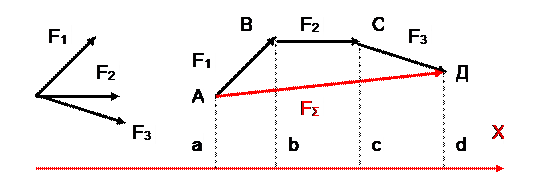
F1X=ab; F2X=bc; F3X=cd
FΣX=ad=ΣFiX
FΣY=ΣFiY
Формула для определения модуля равнодействующей силы через её проекции на оси координат
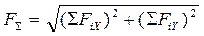
Проекция векторной суммы сил на ось равна алгебраической сумме проекций слагаемых сил на ту же ось.
Аналитическое условие равновесия плоской системы сходящихся сил.
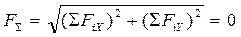
Плоская система сходящихся сил находится в равновесии, когда алгебраические суммы проекций всех сил на две взаимно перпендикулярные оси равны 0.
Уравнения равновесия
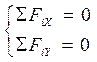
Пространственная система сходящихся сил
Система сил, линии действия которых расположены в различных плоскостях, называется пространственной.
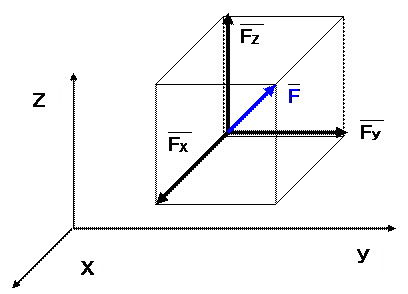
Параллелепипед сил
Силу F можно представить в виде диагонали прямоугольного параллелепипеда, рёбрами которого являются вектора FХ, FУ, FZ, модули которых равны проекциям силы F на соответствующие оси координат X, Y, Z.
Формула для определения силы через её проекции на оси координат:
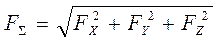
Направляющие косинусы:
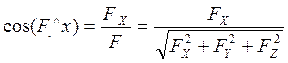 ;
; 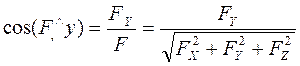 ;
; 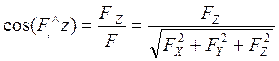
Дата добавления: 2020-10-14; просмотров: 3060;











