Действие данной системы сил на твердое тело не изменяется, если к ней добавить или от нее отнять уравновешенную систему сил.
Следствие 1: Силу, приложенную к твердому телу, можно переносить вдоль линии ее действия в любую другую точку, действие силы на тело при этом не изменится. Таким образом, сила, приложенная к твердому телу, – скользящий вектор.
Доказательство:
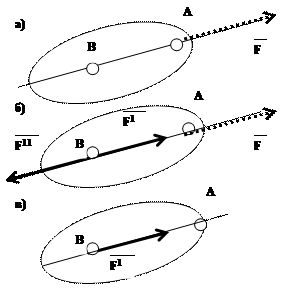Допустим, что к твердому телу в точке А приложена сила F и требуется перенести эту силу в точку В, лежащую на линии действия силы (рис. а).
Приложим к телу в точке В вдоль линии действия силы F уравновешенные силы F1 и F11 (рис. б), численно равные силе F. По аксиоме 3 действие силы F при этом не нарушится.
По аксиоме 2, силы F и F11 уравновешивают друг друга, а по 3-ей аксиоме их можно исключить из получившейся системы сил (рис. в).
Оставшаяся сила F1, приложенная в точке В, численно равна силе F (F1=F) и направлена вдоль той же прямой, то есть векторы F1 и F равны , а это равносильно тому, что сила F из точки А вдоль линии её действия перенесена в точку В.
Аксиома 4 (правило параллелограмма).
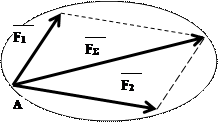Две приложенные к точке тела силы имеют равнодействующую, приложенную в той же точке и равную диагонали параллелограмма, построенного на этих силах, как на сторонах.
Операцию замены системы сил их равнодействующей называют сложением сил.
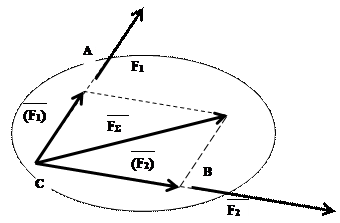Если две силы F1 и F2 приложены к разным точкам тела, но линии их действия лежат в одной плоскости, то, имея в виду, что сила – скользящий вектор, можно, как показано на рисунке, силы F1 и F2 из точек А и В по линиям их действия перенести в точку С их пересечения, а затем сложить по правилу параллелограмма.
Геометрически равнодействующую двух сил можно определить, построив вместо параллелограмма сил треугольник сил.
Аксиома 5 (закон равенства действия и противодействия).
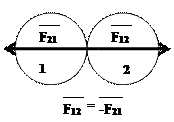Силы взаимодействия двух твёрдых тел друг на друга равны по модулю, но действуют вдоль одной прямой в противоположные стороны.
Тело 1 действует на тело 2 с силой F12, тело 2 действует на тело 1 с силой F21, направленной противоположно. │F12│=│F21│.
Эти силы не уравновешивают друг друга, так как приложены к разным телам.
В физике эта аксиома известна как третий закон Ньютона.
Аксиома 6 (принцип отвердевания).
Если деформируемое (не абсолютно твердое) тело, находится в равновесии, то равновесие этого тела не нарушится, если, не изменяя формы, размеров, положения в пространстве, оно превратится в абсолютно твердое тело, то есть затвердеет.
Связи и их реакции
Твердое тело называют свободным, если оно может перемещаться в пространстве в любом направлении (летящий воздушный шар).
Твердое тело называют несвободным, если его перемещение в пространстве ограничено какими-либо другими телами.
Все тела, которые так или иначе ограничивают перемещение данного несвободного тела, называют связями.
Например, перемещение стула, стоящего на полу, ограничивается полом, для стула пол является связью. Движение шара ограничивается нитью (для шара связью служит нить).
Между несвободным телом и телом, осуществляющим связь, появляются силы взаимодействия.
Сила, с которой связь действует на рассматриваемое тело, препятствуя его перемещению в том или ином направлении, называется реакцией связи.
Силы взаимодействия тела и связи зависят от других сил, приложенных к несвободному телу. Эти силы называют активными (или нагрузками) (например, сила тяжести). Как правило, они известны или заданы.
Для определения реакций связи используют принцип освобождаемости от связей: не изменяя равновесия тела, каждую связь можно отобразить, заменив её реакцией.
Задача определения реакций связей – одна из основных задач статики, так как знание этих сил необходимо для создания прочных и работоспособных конструкций.
Реакции связей приложены к телу в точках соприкосновения тела со связью и направлены в сторону, противоположную той, куда связь не дает перемещаться телу.
Направление реакции связи зависит от типа связи, её расположения относительно тела и характера соприкосновения или соединения связи с телом.
Дата добавления: 2020-10-14; просмотров: 1007;
Поиск по сайту
Узнать еще
- Andantino con moto А. Бородин. Для берегов отчизны дальней
- ATA/133 (Parallel ATA, UltraDMA/133 или E-IDE)
- E) Расчет структурных составляющих очага деформации с одним нейтральным сечением
- F06 Другие психические расстройства вследствие повреждения или дисфункции головного мозга, либо вследствие физической болезни
- F45.38 другие органы или системы
- F52 Половая дисфункция, не обусловленная органическим расстройством или заболеванием
- Hа pазpезе показывают то, что расположено в секущей плоскости и что pасположено за ней.
- I. Идентификация потенциально вредных и (или) опасных факторов на рабочих местах.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
