ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

В данном учебном пособие приводятся в очень упрощенной форме идеи нескольких методов математического программирования, наиболее часто применяемых для поиска оптимальных экономических решений. Предполагается, что постановка задачи поиска оптимального решения и решение самой задачи осуществляется совместно экономистом и математиком-исследователем. Экономист знает идеи основных математических методов и формулирует задачу в экономических категориях. Математик-исследователь осуществляет перевод экономических категорий на язык формул, выбирает математический метод решения задачи и осуществляет его программную реализацию. Довольно часто задачи поиска оптимальных экономических решений имеют несколько критериев оптимальности. Критерии оптимальности и ограничения задаются линейными или нелинейными функциями.

На практике постоянно встречаются такие ситуации, когда достичь какого-то результата можно не одним, а многими различными способами. В подобной ситуации может оказаться и одно предприятие и целая отрасль, если необходимо определить, как использовать имеющиеся в их распоряжении ресурсы, чтобы добиться максимального выхода продукции. Естественно, при большом количестве решений выбирается наилучшее. Математически это обычно сводится к нахождению наибольшего и наименьшего значения некоторой функции, то есть к задаче: найти max (min) f(x), при условии, что переменная x пробегает данное множество X.

Записывают так: f(x) 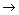max (min), x 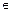X.

Определенная таким образом задача называется задачей оптимизации. Множество Х называется допустимым множеством, а f(x) – целевой функцией.

Очень многое зависит от того, в каком виде задается множество Х.

Чаще всего это система неравенств: ,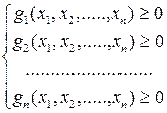

где (x₁,x₂,….,x_n) – координаты точки х в R_n (n-мерном пространстве), а g_i – некоторые функции. Таким образом, надо найти экстремум функции f(x) при заданной системе ограничений. Но понятно, что следует найти не только само значение max (min), но и точку (или точки, если их несколько), в которых это значение достигается. Такие точки называются оптимальными решениями. Задачи подобного рода называются задачами математического программирования.

В большинстве случаев в число ограничений входят условия неотрицательности переменных: x₁ ≥ 0, x₂ ≥ 0,…., x_n ≥ 0, которые вытекают из реального экономического смысла этих чисел и называются тривиальными ограничениями.

В зависимости от характера функций f,g₁, g₂,….g_n различают разные виды математического программирования. Наиболее простой и часто встречающийся случай, который мы и будем изучать, – когда эти функции являются линейными, то есть каждая из них имеет вид 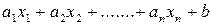. Тогда говорят о задаче линейного программирования. Линейное программирование оформилось как отдельный раздел прикладной математики в 40–50 гг. ХХ века, когда выяснилось, что целый ряд задач из сферы планирования и управления может быть сформулирован в виде задачи линейного программирования. Подсчитано, что в настоящее время ≈ 80–85 % всех решаемых на практике задач оптимизации относится к задачам линейного программирования.