Решение задачи линейного программирования

методом последовательного улучшения плана

(симплексным методом)

Симплексным методом можно решить любую задачу линейного программирования с произвольным числом переменных и ограничений. Для того чтобы решить задачу симплексным методом, ее надо привести к каноническому виду. Напомним, что любую задачу линейного программирования можно привести к каноническому виду:

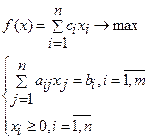
Пример решения задачи. Прибыль от реализации 1 т кефира составляет 2 млн руб., а от 1 т молока – 1 млн руб. Затраты рабочего времени на молоко 4 ч / т, а на кефир – 2 ч/т. Рабочий день – 8 часов. Расход сырья: 5 ед. на 1 т кефира и 1 ед. на 1 т молока. Всего имеется в запасе 5 ед. сырья. Составить такой план производства продукции, чтобы прибыль от ее реализации была максимальной.

Экономико-математическая модель задачи будет иметь вид:

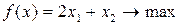
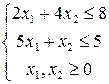
Приведем ее к каноническому виду: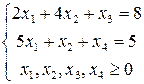

Значения дополнительных переменных показывают разницу между запасами ресурсов каждого вида и их потреблением, то есть остатки ресурсов.

Выразим переменные:

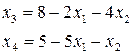
Если 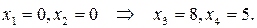Этот план можно взять в качестве начального решения задачи

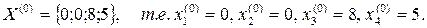
Этот план обладает тем свойством, что число его переменных, не равных нулю, равно числу неравенств в системе ограничений задачи. Такой план называется опорным. Его можно получить в том случае, если часть переменных удается выразить через остальные, причем если приравнять нулю переменные, стоящие в этих выражениях справа, то переменные, стоящие слева, окажутся положительными.

Положительные переменные, стоящие слева, принято называть базисными, а переменные, стоящие справа и приравниваемые нулю, – свободными.

Для каждого опорного плана целевая функция преобразуется так, чтобы она зависела только от свободных переменных.

Для нашего опорного плана в f(x) базисные переменные не входят и для него f(x)=0.

На каждой итерации (на каждом шаге) может увеличиваться лишь одна свободная переменная. Это приводит к увеличению f(x), если перед этой переменной стоит знак «+».

Так как в нашей целевой функции перед обеими свободными переменными стоит «+», то можно увеличивать любую из них и это приведет к увеличению f(x). Выберем x₁, т.к. при ней больше коэффициент, следовательно скорость возрастания целевой функции выше.

При 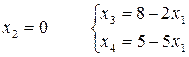, следовательно, при 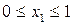значения 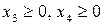, а при х₁ > 1 х₄ станет < 0, что противоречит условию. Т.е. увеличивать х₁ (и при этом уменьшать х₃ и х₄) можно не более чем на 1.

Получили новый план 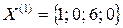, т.е.

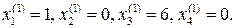
Базисные переменные х₁ и х₃, а свободные х₂ и х₄.

Перепишем систему равенств, выразив базисные переменные и целевую функцию через свободные:

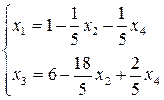
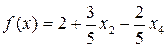
Для нового опорного плана f(x)=2. По f(x) видно, что при увеличении х₄ целевая функция будет убывать, а при увеличении х₂ – возрастать. Следовательно, х₂ вводим в базис.

При 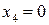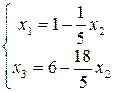. Следовательно, при 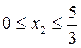значения 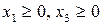, а при х₂>5/3 х₃ станет <0, что противоречит условию. Т.е. увеличивать х₂ (и при этом уменьшать х₁ и х₃) можно не более чем на 5/3.

Получили новый план ,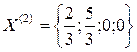

т.е.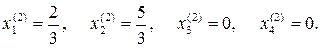

Базисные переменные х₁ и х₂, а свободные х₃ и х₄.

Выразим базисные переменные и линейную форму через свободные переменные

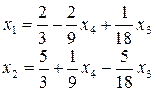
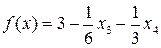
Принимая свободные переменные равными 0 ( 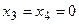), получим f(x)=3. Все коэффициенты в целевой функции отрицательные, следовательно решение найдено (любое увеличение свободных переменных приведет к уменьшению целевой функции, уменьшать их нельзя, так как они равны 0, а отрицательными быть не могут). Базисные же переменные нельзя изменить, не меняя значения свободных. Таким образом, опорный план (2) является оптимальным и максимальное значение целевой функции равно 3.

Ø Важно помнить.Графически можно решать только задачи, которые содержат две переменные, и их необходимо привести к стандартной форме. Симплексным методом можно решать задачи с любым числом переменных, задачу необходимо привести к каноническому виду.

Практические расчеты при решении реальных задач симплексным методом выполняются в настоящее время с помощью компьютеров. В частности, в офисной программе Excel есть встроенная функция «Поиск решения» (закладка Сервис). Однако если расчеты осуществляются без компьютера, то удобно использовать так называемые симплексные таблицы, то есть преобразовывать не сами уравнения, а коэффициенты при переменных. Рассмотрим алгоритм их составления. Для определенности считаем, что решается задача на отыскание максимума.

Таблица 1.6

Исходная таблица решения задачи линейного программирования

симплексным методом

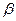
		Х1	Х2	Х3	Х4	Q
Х3						8/2
Х4						5/5
f(x)		–2	–1			–

­

Значения в столбце соответствуют коэффициентам при переменных, 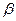– столбец свободных членов.

Строки соответствуют уравнениям задачи, последняя строка – линейная форма, она записывается в виде: f(x)=0 – (–2)x₁ – (–1)x₂.Задача решается до тех пор, пока все коэффициенты в последней строке не станут больше или равны 0.

1 итерация.

В последней строке таблицы находим максимальное по абсолютной величине отрицательное число (= –2). Столбец, в котором стоит это число, называется ведущим. Соответствующая ведущему столбцу свободная переменная (х₁) станет базисной. Делим элементы столбца 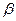на ведущий столбец – записываем значения в столбец Q. Экономический смысл элементов столбца Q: они показывают, на сколько можно увеличить переменную, вводимую в базис, чтобы остальные переменные не стали отрицательными. Из элементов столбца Q выбираем минимальное значение 8/2=4, 5/5=1 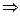min=1, оно соответствует х₄ 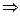строка, соответствующая этой переменной называется ведущей, ведущая строка показывает, какая переменная (в данном примере переменная х₄) станет свободной. Переменная х₁ вместо х₄ становится базисной. На каждом шаге решения количество базисных переменных остается неизменным. Элемент, стоящий на пересечении ведущего столбца с ведущей строкой, называется ведущим элементом.

Ø Важно помнить.При заполнении столбца Q надо делить только на положительные коэффициенты ведущего столбца. Так как если бы один из коэффициентов был отрицателен или равен нулю, соответствующая базисная переменная не стала бы отрицательной ни при каком положительном значении переменной, вводимой в базис.

Заметим, что в данном примере коэффициенты ведущего столбца все положительные (стоящие в строках базисных переменных) 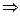обе базисные переменные убывают с увеличением х₁, Пересчитываем таблицу.

Таблица 1.7

Первая итерация

базис		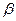Х1	Х2	Х3	Х4	Q
Х3			18/5		–2/5	5\3
Х1			1/5		1/5
f(х)			–3/5		2/5	–

­

1) Вся ведущая строка делится на ведущий элемент.

2) Преобразованная ведущая строка умножается на элемент, стоящий в ведущем столбце строки, которую хотим преобразовать, и вычитается из бывшей строки.

То же самое с линейной формой [(–2) умножить на преобразованную ведущую строку (х₁) и вычесть из бывшей f(х)].

2 итерация.

В последней строке одно число отрицательное (–3/5), следовательно это столбец ведущий. В нем оба коэффициента положительные, заполняем столбец Q.

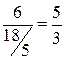Q: и 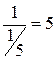. 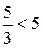, отсюда следует, что ведущая строка первая; ведущий элемент 18/5, переменная x₂ становится базисной, а x₃ – свободной.

Пересчитываем таблицу.

Таблица 1.8

Вторая итерация

базис		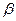X1	X2	X3	X4
X2	5/3			5/8	–1/9
X1	2/3			–1/18	2/9
f(x)				1/6	1/3

Все элементы последней строки не отрицательные, следовательно задача решена.

f(x)= 3 – 1/6x₃ – 1/3x₄ , x₂=5/3, x₁=2/3, f_max=3.

Алгоритм:

1) Проверка оптимальности. Если все элементы последней строки таблицы неотрицательны, то план оптимален.

Если в последней строке есть отрицательные элементы, перейти к пункту 2.

2) Выбор ведущего столбца. В последней строке таблицы найти максимальный по абсолютному значению отрицательный элемент. Столбец, в котором находится этот элемент, будет ведущим.

3) Нахождение ведущей строки. Разделить элементы столбца 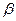на соответствующие положительные элементы ведущего столбца и найти минимальное из этих отношений. Строка, соответствующая этому минимальному отношению, будет ведущей. Элемент, расположенный на пересечении ведущего столбца и ведущей строки, – ведущий.

4) Преобразование таблицы. Разделить ведущую строку на ведущий элемент. Остальные строки таблицы преобразовываются по следующим правилам: пусть надо преобразовать i-ю строку, для этого необходимо умножить преобразованную ведущую строку на элемент i-й строки и ведущего столбца и результат вычесть из i-й строки. В преобразованной таким образом таблице изменить номера базисных переменных: ведущей строке будет соответствовать теперь номер ведущего столбца.

Ø Важно помнить.В качестве основных переменных на первом шаге удобно выбирать (если возможно) такие m переменных, каждая из которых входит только в одно из уравнений системы ограничений.

Положительное значение остаточной переменной указывает на неполное использование соответствующего ресурса, т. е. данный ресурс является недефицитным. Если же остаточная переменная равна нулю, это свидетельствует о полном потреблении соответствующего ресурса. В случае недефицитности любое увеличение ресурсов сверх установленного максимального значения привело бы лишь к тому, что они стали бы еще более недефицитными. Оптимальное решение задачи при этом осталось бы неизменным.