Формулировка задачи и ее геометрическое истолкование
Чтобы показать, как решить задачу графическим способом, необходимо ввести некоторые понятия. Любое x 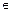 X называется допустимым решением (планом). Допустимое решение, дающее max (min) f(x),называется оптимальным решением (планом). Неравенства называются ограничениями. Решение системы всех неравенств называется областью допустимых решений. Задачи на max и min идентичны, так как они сводятся друг к другу путем умножения целевой функции на (–1), то есть max f(x)= – min (–f(x)).
X называется допустимым решением (планом). Допустимое решение, дающее max (min) f(x),называется оптимальным решением (планом). Неравенства называются ограничениями. Решение системы всех неравенств называется областью допустимых решений. Задачи на max и min идентичны, так как они сводятся друг к другу путем умножения целевой функции на (–1), то есть max f(x)= – min (–f(x)).
Таким образом, необходимо найти оптимальное значение функции (минимум или максимум) в области допустимых решений.
Наиболее часто встречаются две разновидности задач линейного программирования:
1. Каноническая (основная). Система ограничений, помимо тривиальных ограничений, включает в себя только уравнения.
2. Стандартная (симметричная). Система ограничений состоит только из неравенств.
В зависимости от способа решения задачи, необходимо, чтобы она была представлена в той или другой форме.
Эти две разновидности легко сводятся одна к другой.
Пример решения задачи:
1. Стандартный вид Канонический вид
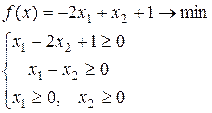
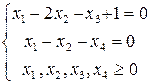
2. Канонический вид

Решая систему линейных уравнений, получим: 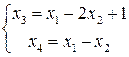 . Подставляя найденные значения в целевую функцию и исключая найденные переменные из системы ограничений, получим стандартный вид задачи линейного программирования:
. Подставляя найденные значения в целевую функцию и исключая найденные переменные из системы ограничений, получим стандартный вид задачи линейного программирования:

Множество решений (планов) основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин (то есть для одного из опорных планов) значение целевой функции является оптимальным, то есть max (min). Если значение max (min) функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин. Иными словами, если оптимальное значений функции достигается в двух вершинах многоугольника, то оно будет одинаковым не только в этих вершинах, но и в любой точке отрезка, соединяющего эти вершины.
Вершину многогранника решений найти сравнительно просто, если задача, записанная в стандартной форме, содержит не более двух переменных, так как в этом случае многогранник можно изобразить на плоскости, вершина находится как точка пересечения двух прямых, которые задают ограничения в системе.
Пример решения задачи. 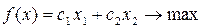


Рис. 1.1. Задача имеет Рис. 1.2. Целевая функция
единственное решение не ограничена


Рис. 1.3. Система ограничений Рис. 1.4. Максимальное значение
несовместна функция принимает на отрезке АВ
Пример решения задачи.
Найти max и min функции  при заданной системе ограничений:
при заданной системе ограничений:

Построим многоугольник решений:

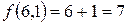
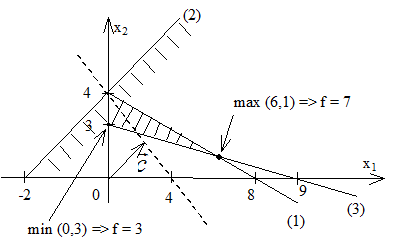
Рис. 1.5. Решение задачи графическим методом
Задание для самостоятельной работы. Решить задачу линейного программирования графическим способом.
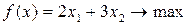
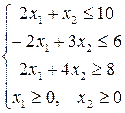
Дата добавления: 2020-10-14; просмотров: 507;











