Метод множителей Лагранжа

Пусть задача математического программирования задана в виде

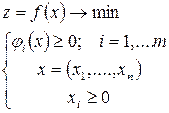, (1.1)

то есть все функциональные ограничения – неравенства и присутствует ограничение на неотрицательность для переменных задачи.

Если исходная задача оптимизации имеет другой вид, то она может быть к нему приведена (тип неравенств и экстремума целевой функции меняют умножением на (–1), а добавление в левую часть равенства дополнительной переменной q ³ 0 избавит задачу от наличия в ней равенства).

Следующую функцию переменных x, l₁,...,l_n называют функцией Лагранжа задачи (1.1):

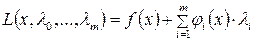(1.2)

Функция Лагранжа представляет собой линейную комбинацию целевой функции и функций, определяющих ограничения задачи. Коэффициенты l₁,..., l_m линейной комбинации называются множителями Лагранжа.

Седловой точкой функции Лагранжа задачи (1.1) называется такая точка (x^*, l^*) (m + n)-мерного пространства переменных x₁,..., x_n; l₁,...,l_m, x ³ 0, l ³ 0, в которой для функции Лагранжа выполнены условия:

L(x, l^*) £ L(x^*, l^*) £ L(x^*, l) для всех x ³ 0, l³ 0.

Иными словами, в седловой точке достигается максимальное значение функции Лагранжа по переменным группы x (исходным переменным задачи (1.1)) и минимальное значение по переменным группы l.

Необходимые условия экстремума для функции Лагранжа в случае дифференцируемости целевой функции и функций, определяющих ограничения задачи, состоят в равенстве нулю всех ее частных производных. Дифференцируя L(x, l) по всем переменным, получим следующие соотношения:

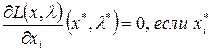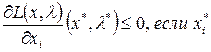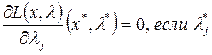>0

=0

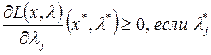>0

=0

Для дальнейших целей данные соотношения удобнее представить в виде условий дополняющей нежесткости:

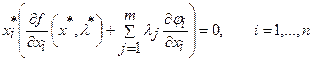
Если функция Лагранжа задачи (1.1) имеет седловую точку (x^*, l^*) при неотрицательных значениях x ³ 0, l ³ 0, то вектор x является решением поставленной задачи оптимизации. Использование данного факта для поиска оптимальных решений исходной задачи состоит в поиске седловых точек функции Лагранжа и носит название метода множителей Лагранжа.

Пример решения задачи. Гражданин Петров собирается разместить денежные средства (в пределах 100 ден. ед.) в банк. Банк предлагает два вида срочных вкладов. Согласно первому варианту деньги могут быть размещены на год, и доход составит 20 % годовых. Второй вариант предполагает, что деньги могут быть получены через два года и доход по данному виду вкладов составляет 25 % годовых. Предпочтения гр. Петрова описывает функция полезности

.

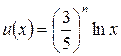Требуется определить, как гр. Петров разместит деньги.

Решение.Первый шаг состоит в формальном представлении задачи – формализации, основные шаги которой состоят в определении переменных, ограничений, показателей эффективности и соответствующих им целевых функций.

Переменные.Альтернатива выбора гр. Петрова состоит в том, сколько денег разместить и в какой вид услуги. Пусть x₁, x₂ – объемы денежных средств, которые гр. Петров разместит в 1-й и 2-й виды предлагаемых вкладов.

Ограничения. Гр. Петров собирается потратить не более 100 ден. ед., следовательно x₁ + x₂ £ 100. Кроме того, не имеют смысла отрицательные значения переменных, то есть x₁, x₂ ³ 0.

Показатели эффективности. Принимая решение о размещении денежных средств, гр. Петров стремится максимизировать полезность от получаемых денежных средств. Таким образом, определен показатель эффективности – полезность денег. Гр. Петров получит деньги трижды. Первый раз – это величина средств, оставшихся после размещения денег во вклады. Она составляет 100 – x₁ – x₂, а ее полезность 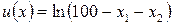. Далее, в конце первого года завершит свое действие 1-й вид услуги, и гр. Петров получит 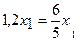ден. ед., полезность которых с позиции текущего дня для него составляет 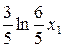. И наконец, по истечении срока действия второго договора (в конце второго года) бюджет гр. Петрова пополнит сумма в размере 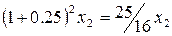, полезность которой составляет в настоящий момент величину 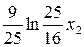. Таким образом, принимаемое решение приносит гр. Петрову суммарную полезность, составляющую

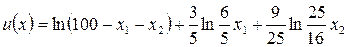. Требуется найти такие значения переменных x₁, x₂, чтобы величина u(x) была максимальной.

Формализованное представление задачи выглядит как

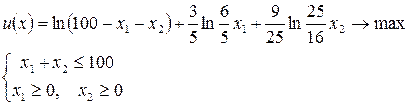
Для нахождения седловой точки составим функцию Лагранжа этой задачи:

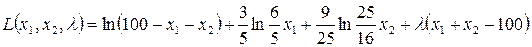
Условия дополняющей нежесткости для данной задачи представляют собой систему из трех уравнений с тремя неизвестными x₁, x₂, l, имеющую вид (в скобках каждого уравнения находятся частные производные функции Лагранжа по соответствующим переменным):

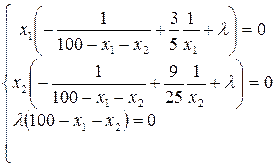
Заметим, что значения x₁ = 0, x₂ = 0 и 100 = x₁ + x₂ являются недопустимыми, так как в этих случаях не определена целевая функция. Условие 100 ¹ x₁ + x₂ влечет за собой l = 0 – третье условие системы дополняющей нежесткости. Следовательно, для нахождения решения достаточно решить систему:

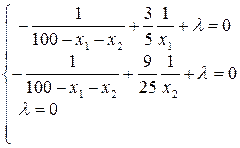
Ее решение: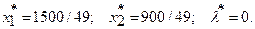

Ответ.Гр. Петров поместит 30,612 ден. ед. в первый вклад и 18,367 ден. ед. во второй вклад.

Ø Важно помнить.Соотношения дополняющей нежесткости являются лишь необходимыми (но не достаточными) условиями седловой точки, то есть соотношения могут быть выполнены в некоторой точке, а экстремума в ней может и не быть.

Экономический смысл множителей Лагранжа

Пусть исходная задача (1.1) является формализованным представлением некоторой экономической ситуации. К задаче математического программирования приводят задачи, в которых требуется принять решение о выборе одной из допустимых альтернатив (планов), наилучшей в смысле некоторого критерия эффективности. Искомой альтернативе в задаче соответствуют переменные x. Функциональные зависимости между переменными описывают взаимодействия и взаимозависимости различных компонентов альтернативы выбора, а также представляют собой оценки затрат, необходимых для реализации той или иной альтернативы. Наличие каких-либо лимитов на ресурсы влечет за собой ограничения на выбор альтернативы. Для простоты будем считать, что все ограничения задачи (1.1) соответствуют лимитам на ресурсы, требующиеся для реализации выбираемой альтернативы.

Условия дополняющей нежесткости представляют собой систему уравнений, каждое из которых является произведением двух сомножителей. Рассмотрим одно уравнение второй группы, например 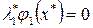. Понятно, что его решение можно представить как решение системы:

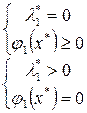
Множитель Лагранжа 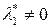соответствует границе допустимого множества, определяемой функцией j₁(x^*) = 0. Иными словами, если 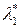не равен нулю, то решение принадлежит границе, определяемой уравнением j₁(x^*) = 0. Это, в свою очередь, означает, что для оптимальной альтернативы x^* первый ресурс (его затраты описывает функция j₁(x)) является "узким местом" – будет израсходован полностью. Изменение имеющегося лимита для этого ресурса повлечет за собой достижение более высокого значения показателя эффективности. Если множитель Лагранжа, соответствующий первому ограничению, равен нулю, то в соответствии с (1.2) j₁(x^*) ³ 0. Это означает, что x^* не находится на границе, задаваемой функцией j₁(x^*) = 0, и первоначальные лимиты на первый ресурс завышены (занижены). В частности, в решенном примере l = 0 соответствует ограничению на расход денег гр. Петровым и означает, что в оптимальном для себя случае этот гражданин не истратит всех своих средств, приобретая банковские услуги. Остаток средств составит 100 – (30,612+18,367) = 51,02, и именно такое распределение денег принесет Петрову максимальную полезность. Если ограничению соответствует ненулевой множитель Лагранжа l = 1, что означает, что в оптимальном плане данный ресурс будет израсходован полностью.

Пусть l_i > 0. Экономический смысл абсолютной величины множителя Лагранжа не очень прост и привязан к контексту задачи. Наиболее наглядно можно продемонстрировать его на примере задач об оптимизации производства. Пусть целевая функция F(x) некоторой задачи описывает выпуск x = (x₁,..., x_n)^тn видов готовой продукции, а ограничения соответствуют затратам производственных факторов, используемых в некоторой производственной системе. Лимиты для m невоспроизводимых производственных ресурсов заданы как b = (b₁,..., b_m). Модель такой задачи имеет вид:

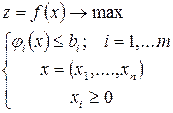
Каждому лимитированному производственному фактору соответствует множитель Лагранжа l_i ³ 0. Кроме того, ненулевые множители Лагранжа показывают, какие из производственных факторов в оптимальном плане будут израсходованы целиком, что в некотором роде ограничивает возможность дальнейшего увеличения выпуска. Посмотрим, как изменяется оптимальное решение (план) при малых изменениях лимитирующих величин b_i. Иными словами, мы предположили, что оптимальный выпуск есть функция от запаса ресурса: x(b) = (x₁(b),..., x_n(b)). Показатель эффективности F(b) = F(x(b)) при этом является сложной функцией лимитов ресурсов. Все ограничения представляют собой функциональные соотношения компонентов выпуска x и, следовательно, также являются сложными функциями j_i(x(b)) лимитов b.

Множитель Лагранжа l_i определяет прирост оптимальной величины выпускаемой продукции при изменении запаса i-го ресурса на "малую величину": 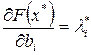. Одновременно l_i представляет собой верхний предел цены ресурса, которую предприятие согласно заплатить, если оно имеет в виду безубыточное его использование. Действительно, пусть прирост выпуска обеспечивается за счет прироста запаса i-го ресурса на db_i (запасы остальных ресурсов неизменны). Соответствующий прирост выпуска составит 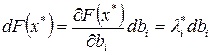. Если цена единицы данного ресурса q_i, то прирост затрат составит q_i db_i. Отсюда видно, что при l_i > q_i прирост выпуска превышает прирост затрат и l_i = q_i означает, что прирост выпуска совпадает с приростом затрат, что и объясняет смысл верхнего предела цены единицы ресурса.