Задач линейного программирования
1.Задача об использовании ресурсов (планировании производства).
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Введем следующие обозначения:
хj – число единиц продукции Pj , запланированной к производству,
bi – запас ресурса Si ,
aij – число единиц ресурса Si , затрачиваемое на единицу продукции Pj (эти числа называют технологическими коэффициентами),
cj – прибыль от реализации продукции Pj .
Тогда модель задачи будет иметь вид:
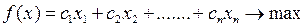
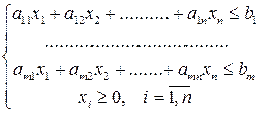
Рассмотрим задачу с конкретными данными.
Прибыль от реализации единицы продукции Р1 составляет 2 рубля, а от единицы продукции Р2 – 3 рубля. Данные о запасах ресурсов и количестве ресурсов, необходимых для изготовления единицы продукции, сведены в следующую таблицу.
Таблица 1.1
Данные задачи об использовании ресурсов
| Вид ресурса | Запас ресурса | Число единиц ресурса, затрачиваемых на изготовление единицы продукции | |
| Р1 | Р2 | ||
| S1 | |||
| S2 | |||
| S3 | --- | ||
| S4 | --- |
Экономико-математическая модель данной задачи будет иметь вид:
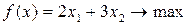
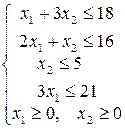
2.Задача составления рациона (о диете, о смесях), или технологическая задача.
Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.
Введем обозначения:
xj – число единиц корма j-го вида;
bi – необходимый минимум содержания в рационе питательного вещества Si ;
aij – число единиц питательного вещества Si в единице корма j-го вида;
cj – стоимость единицы корма j-го вида.
Тогда экономико-математическая модель задачи запишется следующим образом:
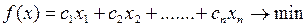
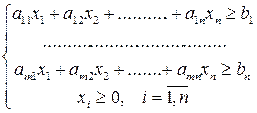
Рассмотрим задачу с конкретными данными.
Стоимость 1 кг корма вида I – 4 рубля, а вида II – 6 рублей. Используя данные таблицы, необходимо составить такой рацион питания, чтобы стоимость его была минимальной и содержание каждого вида питательных веществ было не менее установленного предела.
Таблица 1.2
Данные задачи о рационе питания
| Питательное вещество | Необходимый мин. пит. веществ | Число единиц питательного вещества в 1 кг корма | |
| I | II | ||
| S1 | |||
| S2 | |||
| S3 |
Модель задачи будет иметь вид:
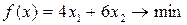
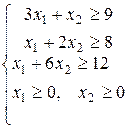
3.Задача об использовании мощностей (задача о загрузке оборудования).
Предприятию задан план производства продукции по времени и номенклатуре: требуется за время Т выпустить n1, n2,……nk единиц продукции P1, P2,……Pк. Продукция производится на станках S1, S2, …….Sm. Для каждого станка известны производительность aij (то есть число единиц продукции Pj , которое можно произвести на станке Si в единицу времени) и затраты bij на изготовление продукции Pj на станке Si в единицу времени.
Необходимо составить такой план работы станков (то есть так распределить выпуск между станками), чтобы затраты на производство всей продукции были минимальными.
Экономико-математическая модель задачи.
Обозначим xij – время, в течение которого станок Si будет занят изготовлением продукции Pj . Так как время работы каждого станка ограничено и не превышает Т, то справедливы следующие неравенства:
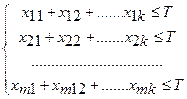
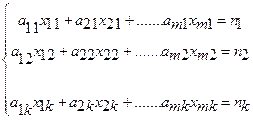
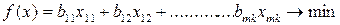
4.Технологическая задача (о раскрое материала).
Найти план раскроя, обеспечивающий максимальное число комплектов.
Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступает 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов.
Составим модель задачи.
Определим сначала все возможные способы распила бревен, указав соответствующее число получающихся при этом брусьев и остаток.
Таблица 1.3
Способы распила бревен
| Способ распила | Число получающихся брусьев | Остаток | ||
| 1,2 м | 3 м | 5 м | ||
| -- | -- | |||
| -- | 0,6 | |||
| -- | -- | |||
| -- | -- |
Через хi обозначим число бревен распиливаемых i-м способом, 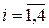 , а через х – число комплектов брусьев.
, а через х – число комплектов брусьев.
Тогда экономико-математическая модель задачи будет иметь вид:
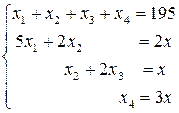
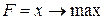
Задания для самостоятельной работы.
1. Имеем 195 бревен длиной 6 метров. Составить модель распила бревен, если необходимо получить 50 брусьев длиной 2 м, 75 брусьев длиной 3 м и 60 брусьев длиной 5 м и требуется минимизировать остатки.
2. Составить экономико-математическую модель задачи и решить ее графическим способом. Для производства двух видов изделий А и В предприятие использует два вида сырья. Данные о количестве расхода сырья и его запасы приведены в таблице. Требуется составить такой план выпуска изделий А и В, чтобы прибыль от их реализации была максимальной.
Таблица 1.4
Данные о расходе и запасах сырья
| Вид сырья | Норма расхода сырья (кг) на одно изделие | Общее кол-во сырья | |
| А | В | ||
| I | |||
| II | |||
| III | |||
| Прибыль от реализации одного изделия |
3. По данным таблицы составить такой план загрузки станков, чтобы затраты были минимальными. Решить задачу графическим способом.
Таблица 1.5
Данные о производительности работы станков
| Тип аппарата | Производительность работы линии (шт.) | План | |
| I | II | ||
| А | |||
| В | |||
| С | |||
| Затраты ден. ед. за шт. |
Дата добавления: 2020-10-14; просмотров: 596;











