Детерминированные модели принятия решений и динамическое программирование
2.1. Рекуррентная природа вычислений динамического программирования.
Динамическое программирование есть особый метод оптимизации решений, специально приспособленный к так называемым «многошаговым» или «многоэтапным» операциям. Динамическое программирование (ДП) определяет оптимальное решение 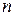 мерной задачи путем ее декомпозиции на
мерной задачи путем ее декомпозиции на 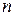 этапов, каждый из которых представляет подзадачу относительно одной переменной. Вычислительное преимущество такого подхода состоит в том, что мы занимаемся решением одномерных оптимизационных подзадач вместо большой
этапов, каждый из которых представляет подзадачу относительно одной переменной. Вычислительное преимущество такого подхода состоит в том, что мы занимаемся решением одномерных оптимизационных подзадач вместо большой 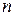 - мерной задачи. Фундаментальным принципом ДП, составляющим основу декомпозиции задачи, является оптимальность. Так как природа каждого этапа решения зависит от конкретной оптимизационной задачи, ДП не предлагает вычислительных алгоритмов непосредственно для каждого этапа. Вычислительные аспекты решения оптимизационных подзадач на каждом этапе проектируются и реализуются по отдельности (что, конечно, не исключает применения единого алгоритма для всех этапов).
- мерной задачи. Фундаментальным принципом ДП, составляющим основу декомпозиции задачи, является оптимальность. Так как природа каждого этапа решения зависит от конкретной оптимизационной задачи, ДП не предлагает вычислительных алгоритмов непосредственно для каждого этапа. Вычислительные аспекты решения оптимизационных подзадач на каждом этапе проектируются и реализуются по отдельности (что, конечно, не исключает применения единого алгоритма для всех этапов).
Вычисления в ДП выполняются рекуррентно в том смысле, что оптимальное решение одной подзадачи используется в качестве исходных данных для следующей. Решив последнюю подзадачу, мы получим оптимальное решение исходной задачи. Способ выполнения рекуррентных вычислений зависит от того, как производится декомпозиция исходной задачи. В частности, подзадачи обычно связаны между собой некоторыми общими ограничениями. Если осуществляется переход от одной подзадачи к другой, то должны учитываться эти ограничения.
Принцип оптимальности. Каково бы ни было состояние системы 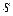 перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.
перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.
Оптимальная стратегия обладает том свойством, что, какими бы ни были начальные состояние и решение, оставшиеся решения образуют оптимальную стратегию для состояния, возникающего после первого перехода.
Представим себе некоторую операцию, состоящую из 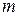 шагов (этапов). Пусть эффективность операции характеризуется каким-то показателем
шагов (этапов). Пусть эффективность операции характеризуется каким-то показателем 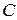 , который мы для краткости будем в этой главе называть «выигрышем». Предположим, что выигрыш
, который мы для краткости будем в этой главе называть «выигрышем». Предположим, что выигрыш 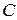 за всю операцию складывается (аддитивный критерий) из выигрышей на отдельных шагах:
за всю операцию складывается (аддитивный критерий) из выигрышей на отдельных шагах:
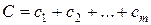 . .
| (2.1) |
где 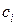 – выигрыш на
– выигрыш на 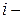 м шаге.
м шаге.
Предполагается, что выигрыш (2.1) в данной операции зависит от некоторого управления. Обозначим его буквой 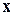 . На каждом шаге выбирается какое-то решение, от которого зависит выигрыш на данном шаге и выигрыш за операцию в целом. Будем называть это решение «шаговым управлением», его обозначим буквами
. На каждом шаге выбирается какое-то решение, от которого зависит выигрыш на данном шаге и выигрыш за операцию в целом. Будем называть это решение «шаговым управлением», его обозначим буквами 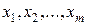 :
:
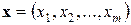 . .
| (2.2) |
Следует иметь в виду, что 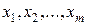 в общем случае – не числа, а, может быть, векторы, функции и т. д.
в общем случае – не числа, а, может быть, векторы, функции и т. д.
Требуется найти такое управление 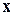 , при котором выигрыш
, при котором выигрыш 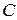 обращается в максимум:
обращается в максимум:
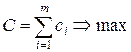 . .
| (2.3) |
То управление 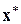 , при котором этот максимум достигается, будем называть оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений:
, при котором этот максимум достигается, будем называть оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений:
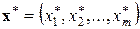 . .
| (2.4) |
Тот максимальный выигрыш, который достигается при этом управлении, мы будем обозначать 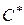 :
:
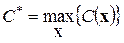 . .
| (2.5) |
Рассмотрим пример многошаговой операции и поясним, что понимается под «управлением» и каков «выигрыш» (показатель эффективности) 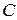 .
.
Пример. Владелец автомашины эксплуатирует ее в течение 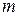 лет. В начале каждого года он может принять одно из трех решений:
лет. В начале каждого года он может принять одно из трех решений:
1) продать машину и заменить ее новой;
2) ремонтировать ее и продолжать эксплуатацию;
3) продолжать эксплуатацию без ремонта.
Шаговое управление — выбор одного из этих трех решений. Непосредственно числами они не выражаются, но можно приписать первому численное значение 1, второму 2, третьему 3. Какие нужно принять решения по годам (т. е. как чередовать управления 1, 2, 3), чтобы суммарные расходы на эксплуатацию, ремонт и приобретение новых машин были минимальны?
Показатель эффективности (в данном случае это не «выигрыш», а «проигрыш», но это неважно) равен
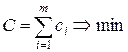 . .
| (2.6) |
где 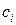 –расходы в
–расходы в 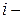 м году. Величину
м году. Величину 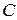 требуется обратить в минимум.
требуется обратить в минимум.
Управление операцией в целом представляет собой какую-то комбинацию чисел 1, 2, 3, например:
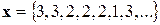 , ,
| (2.7) |
что означает: первые два года эксплуатировать машину без ремонта, последующие три года ее ремонтировать, в начале шестого года продать, купить новую, затем снова эксплуатировать без ремонта и т. д. Любое управление представляет собой вектор (совокупность чисел):
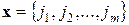 , ,
| (2.8) |
где каждое из чисел 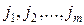 имеет одно из трех значений: 1, 2 или 3. Нужно выбрать совокупность чисел (2.8), при которой величина (2.6) минимальна.
имеет одно из трех значений: 1, 2 или 3. Нужно выбрать совокупность чисел (2.8), при которой величина (2.6) минимальна.
Любую многошаговую задачу можно решать по-разному: либо искать сразу все элементы решения на всех 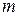 шагах, либо же строить оптимальное управление шаг за шагом, на каждом этапе расчета оптимизируя только один шаг. Обычно второй способ оптимизации оказывается проще, чем первый, особенно при большом числе шагов.
шагах, либо же строить оптимальное управление шаг за шагом, на каждом этапе расчета оптимизируя только один шаг. Обычно второй способ оптимизации оказывается проще, чем первый, особенно при большом числе шагов.
Такая идея постепенной, пошаговой оптимизации и лежит в основе метода динамического программирования. Оптимизация одного шага, как правило, проще оптимизации всего процесса: лучше, оказывается, много раз решить сравнительно простую задачу, чем один раз – сложную.
Принцип динамического программирования отнюдь не предполагает, что каждый шаг оптимизируется отдельно, независимо от других. Напротив, шаговое управление должно выбираться дальновидно, с учетом всех его последствий в будущем. Что толку, если мы выберем на данном шаге управление, при котором эффективность этого шага максимальна, если этот шаг лишит нас возможности хорошо выиграть на последующих шагах?
Значит, планируя многошаговую операцию, надо выбирать управление на каждом шаге с учетом всех его будущих последствий на еще предстоящих шагах. Управление на 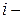 м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей для всех оставшихся до конца шагов.
м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей для всех оставшихся до конца шагов.
Однако из этого правила есть исключение. Среди всех шагов есть один, который может планироваться попросту, без оглядки на будущее. Какой это шаг? Очевидно, последний! Этот шаг, единственный из всех, можно планировать так, чтобы он сам, как таковой, принес наибольшую выгоду.
Поэтому процесс динамического программирования обычно разворачивается от конца к началу: прежде всего, планируется последний, 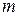 – й шаг. А как его спланировать, если мы не знаем, чем кончился предпоследний? Т. е. не знаем условий, в которых мы приступаем к последнему шагу?
– й шаг. А как его спланировать, если мы не знаем, чем кончился предпоследний? Т. е. не знаем условий, в которых мы приступаем к последнему шагу?
Вот тут-то и начинается самое главное. Планируя последний шаг, нужно сделать разные предположения о том, чем кончился предпоследний, 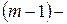 й шаг, и для каждого из этих предположений найти условное оптимальное управление на
й шаг, и для каждого из этих предположений найти условное оптимальное управление на 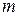 – м шаге («условное» потому, что оно выбирается исходя из условия, что предпоследний шаг кончился так-то и так-то).
– м шаге («условное» потому, что оно выбирается исходя из условия, что предпоследний шаг кончился так-то и так-то).
Предположим, что мы это сделали, и для каждого из возможных исходов предпоследнего шага знаем условное оптимальное управление и соответствующий ему условный оптимальный выигрыш на 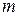 – м шаге. Отлично! Теперь мы можем оптимизировать управление на предпоследнем,
– м шаге. Отлично! Теперь мы можем оптимизировать управление на предпоследнем, 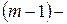 м шаге. Снова сделаем все возможные предположения о том, чем кончился предыдущий,
м шаге. Снова сделаем все возможные предположения о том, чем кончился предыдущий, 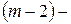 й шаг, и для каждого из этих предположений найдем такое управление на
й шаг, и для каждого из этих предположений найдем такое управление на 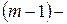 м шаге, при котором выигрыш за последние два шага (из которых
м шаге, при котором выигрыш за последние два шага (из которых 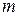 – йуже оптимизирован!) минимален.
– йуже оптимизирован!) минимален.
Так мы найдем для каждого исхода 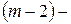 го шага условное оптимальное управление на
го шага условное оптимальное управление на 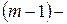 м шаге и условный оптимальный выигрыш на двух последних шагах. Далее, «пятясь назад», оптимизируем управление на
м шаге и условный оптимальный выигрыш на двух последних шагах. Далее, «пятясь назад», оптимизируем управление на 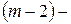 м шаге и т. д., пока не дойдем до первого.
м шаге и т. д., пока не дойдем до первого.
Предположим, что все условные оптимальные управления и условные оптимальные выигрыши за весь «хвост» процесса (на всех шагах, начиная от данного и до конца) нам известны. Это значит: мы знаем, что надо делать, как управлять на данном шаге и что мы за это получим на «хвосте», в каком бы состоянии ни был процесс к началу шага. Теперь мы можем построить уже не условно оптимальное, а просто оптимальное управление 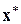 и найти не условно оптимальный, а просто оптимальный выигрыш
и найти не условно оптимальный, а просто оптимальный выигрыш 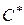 . В самом деле, пусть мы знаем, в каком состоянии
. В самом деле, пусть мы знаем, в каком состоянии 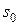 была управляемая система (объект управления
была управляемая система (объект управления 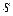 ) в начале первого шага. Тогда мы можем выбрать оптимальное управление
) в начале первого шага. Тогда мы можем выбрать оптимальное управление 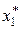 на первом шаге. Применив его, мы изменим состояние системы на некоторое новое
на первом шаге. Применив его, мы изменим состояние системы на некоторое новое 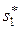 ;в этом состоянии мы подошли ко второму шагу. Тогда нам тоже известно условное оптимальное управление
;в этом состоянии мы подошли ко второму шагу. Тогда нам тоже известно условное оптимальное управление 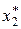 , которое к концу второго шага переводит систему в состояние
, которое к концу второго шага переводит систему в состояние 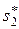 , и т. д. Что касается оптимального выигрыша
, и т. д. Что касается оптимального выигрыша 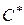 за всю операцию, то он нам уже известен: ведь именно на основе его максимальности мы выбирали управление на первом шаге.
за всю операцию, то он нам уже известен: ведь именно на основе его максимальности мы выбирали управление на первом шаге.
Таким образом, в процессе оптимизации управления методом динамического программирования, многошаговый процесс «проходится» дважды. Первый раз – от конца к началу, в результате чего находятся условные оптимальные управления и условные оптимальные выигрыши за оставшийся «хвост» процесса. Второй раз – от начала к концу, когда нам остается только «прочитать» уже готовые рекомендации и найти безусловное оптимальное управление 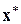 , состоящее из оптимальных шаговых управлений
, состоящее из оптимальных шаговых управлений 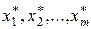 .
.
Первый этап условной оптимизации несравненно сложнее и длительнее второго. Второй этап почти не требует дополнительных вычислений.
2.2. Приложения динамического программирования
Модели динамического программирования обычно применяются при решении задач не очень большого масштаба. Вот некоторые типичные области применения моделей динамического программирования при принятии решений:
- разработка правил управления запасами, устанавливающих момент пополнения запасов и размер пополняющего заказа;
- разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию;
- определение необходимого объема запасных частей, гарантирующего эффективное использование дорогостоящего оборудования;
- распределение дефицитных капитальных вложений между возможными новыми направлениями их использования;
- выбор методов проведения рекламной кампании, знакомящей покупателя с продукцией фирмы;
- систематизация методов поиска ценного ресурса;
- составление календарных планов текущего и капитального ремонта сложного оборудования;
- разработка долгосрочных правил замены выбывающих из эксплуатации основных фондов.
Процессы принятия решений, к которым относятся ряд упомянутых выше моделей, часто относятся к числу микроэкономических. Однако во многих реально функционирующих системах еженедельно требуется принимать тысячи таких решений. В связи с этим модели динамического программирования (ДП) ценны именно тем, что они позволяют принимать миллионы решений на основе стандартного подхода (часто с использованием ЭВМ) при минимальном вмешательстве человека.
2.2.1. Задача об оптимальной загрузке.
Задача о загрузке – это задача о рациональной загрузке автомашины (самолета, судна и т.п.), которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в определении загрузки автомашины такими грузами, которые приносят наибольшую суммарную прибыль.
Перед тем как представить соотношения динамического программирования, заметим, что рассматриваемая здесь задача известна также как задача о снаряжении, где пилот реактивного самолета должен определить наиболее ценные (необходимые) предметы, которые следует взять на борт самолета, или как задача о рюкзаке, в которой турист должен определить наиболее ценные
предметы, подлежащие загрузке в рюкзак.
Основное рекуррентное соотношение динамического программирования выводится для общей задачи загрузки автомашины грузоподъемностью 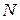 предметами (грузами)
предметами (грузами) 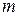 наименований. Пусть
наименований. Пусть 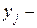 количество предметов
количество предметов 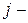 го наименования, подлежащих загрузке,
го наименования, подлежащих загрузке, 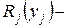 прибыль, которую приносит один загруженный предмет
прибыль, которую приносит один загруженный предмет 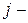 го наименования,
го наименования, 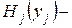 вес одного предмета
вес одного предмета 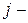 го наименования. Пусть
го наименования. Пусть 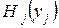 - неубывающие функции, принимающие целочисленные значения и такие, что
- неубывающие функции, принимающие целочисленные значения и такие, что 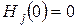 . Тогда задача распределения усилий принимает следующий вид:
. Тогда задача распределения усилий принимает следующий вид:
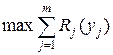
| (2.9) |
при ограничениях:
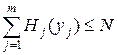 , ,
| (2.10) |
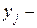 может принимать только целочисленные значения может принимать только целочисленные значения 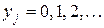 . .
| (2.11) |
При этом на 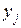 могут быть наложены дополнительные условия в виде ограничения на них сверху
могут быть наложены дополнительные условия в виде ограничения на них сверху
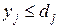 . .
| (2.12) |
Задача (2.9) - (2.12) называется еще задачей распределения усилий. Для того, чтобы свести эту задачу к задаче динамического программирования, обозначим 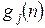 - максимальную суммарную прибыль, полученную при загрузке веса величины
- максимальную суммарную прибыль, полученную при загрузке веса величины 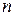 первыми
первыми 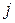 предметами и
предметами и 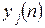 - количество единиц груза
- количество единиц груза 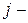 ого вида в случае оптимальной стратегии.
ого вида в случае оптимальной стратегии.
Тогда итерационный процесс вычисления 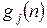 по методу динамического программирования будет выглядеть следующим образом:
по методу динамического программирования будет выглядеть следующим образом:
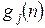 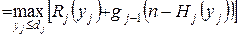 , ,
| (2.13) |
где
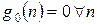 , , 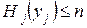 , , 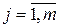 , , 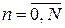 . .
| (2.14) |
Таким образом, процесс решения задачи (2.9) - (2.12) сводится к рекуррентным вычислениям по формулам (2.13) - (2.14). Зная, что 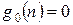 , последовательно вычисляем
, последовательно вычисляем 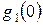 ,
, 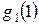 ,...,
,..., 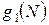 и соответствующие им значения
и соответствующие им значения 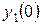 ,
, 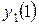 ,...,
,..., 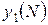 . Затем переходим к шагу 2 и вычисляем
. Затем переходим к шагу 2 и вычисляем 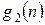 ,
, 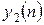 и так, пока
и так, пока 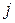 не станет равным
не станет равным 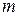 .
.
Пример. Решим задачу распределения усилий общего вида, при следующих данных. Пусть 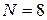 единиц товара и имеется 3 магазина -
единиц товара и имеется 3 магазина - 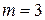 . Пусть прибыль определяется соотношениями:
. Пусть прибыль определяется соотношениями:
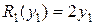 ,
, 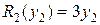 ,
, 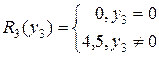
и товар упакован в каждый из магазинов в соответствии со следующими равенствами
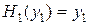 ,
, 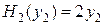 ,
, 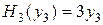 .
.
Кроме того, будем считать, что все 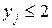 . Требуется так распределить товар по магазинам, чтобы суммарная прибыль была максимальной.
. Требуется так распределить товар по магазинам, чтобы суммарная прибыль была максимальной.
Решение. На нулевом шаге при 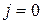 никакого распределения не происходит, и
никакого распределения не происходит, и 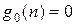
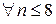 . Рассмотрим шаг
. Рассмотрим шаг 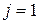 . На этом шаге:
. На этом шаге: 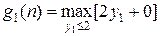 и должно выполняться ограничение
и должно выполняться ограничение 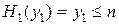 . Результаты вычислений сведем в таблицу 3.
. Результаты вычислений сведем в таблицу 3.
Шаг 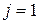
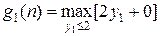
Таблица 3
| n | 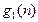
| 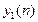
|
| 0 | 0 | 0 |
| 1 | 2 | 1 |
| 2 | 4 | 2 |
| 3 | 4 | 2 |
| 4 | 4 | 2 |
| 5 | 4 | 2 |
| 6 | 4 | 2 |
| 7 | 4 | 2 |
| 8 | 4 | 2 |
Пусть теперь 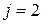 . При этом,
. При этом, 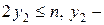 целое. Тогда:
целое. Тогда:
Шаг 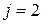 ,
, 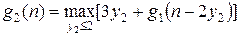 .
.
Таблица 4
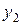 n
n
| 0 | 1 | 2 | 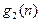
| 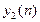
|
| 0 | 0+0 | 0 | 0 | ||
| 1 | 0+2 | 2 | 0 | ||
| 2 | 0+4 | 3+0 | 4 | 0 | |
| 3 | 0+4 | 3+2 | 5 | 1 | |
| 4 | 0+4 | 3+4 | 6+0 | 7 | 1 |
| 5 | 0+4 | 3+4 | 6+2 | 8 | 2 |
| 6 | 0+4 | 3+4 | 6+4 | 10 | 2 |
| 7 | 0+4 | 3+4 | 6+4 | 10 | 2 |
| 8 | 0+4 | 3+4 | 6+4 | 10 | 2 |
При 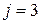 ограничения имеют вид
ограничения имеют вид 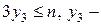 целые. Результаты расчетов поместим в таблице 5.
целые. Результаты расчетов поместим в таблице 5.
Шаг 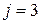 ,
, 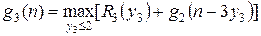 .
.
Таблица 5
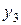 n
n
| 0 | 1 | 2 | 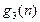
| 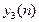
|
| 0 | 0+0 | 0 | 0 | ||
| 1 | 0+2 | 2 | 0 | ||
| 2 | 0+4 | 4 | 0 | ||
| 3 | 0+5 | 4.5+0 | 5 | 0 | |
| 4 | 0+7 | 4.5+2 | 7 | 0 | |
| 5 | 0+8 | 4.5+4 | 8.5 | 1 | |
| 6 | 0+10 | 4.5+5 | 4.5+0 | 10 | 0 |
| 7 | 0+10 | 4.5+7 | 4.5+2 | 11.5 | 1 |
| 8 | 0+10 | 4.5+8 | 4.5+4 | 12.5 | 1 |
Процесс выбора оптимальных значений 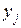 начинается с последней строки табл. 5. Так как
начинается с последней строки табл. 5. Так как 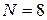 , то из последней строки табл. 5 находим, что
, то из последней строки табл. 5 находим, что 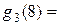 12.5 руб. (при этом
12.5 руб. (при этом 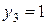 ). Отсюда следует, что
). Отсюда следует, что 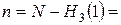 8 - 3 = 5 и поэтому при
8 - 3 = 5 и поэтому при 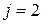 решение выбирается из строки
решение выбирается из строки 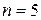 табл. 4, откуда получаем
табл. 4, откуда получаем 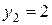 . Тогда оставшееся число товара
. Тогда оставшееся число товара 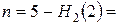 5 – 4 = 1 и
5 – 4 = 1 и 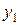 , определяется из табл. 3 при
, определяется из табл. 3 при 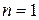 , то есть
, то есть 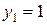 . Таким образом, в первый магазин необходимо отправить одну упаковку с 1 штукой товара, во второй магазин 2 упаковки – 4 штуки и в третий, 1 упаковку с 3 штуками товара. Максимальная прибыль составит 12.5 руб.
. Таким образом, в первый магазин необходимо отправить одну упаковку с 1 штукой товара, во второй магазин 2 упаковки – 4 штуки и в третий, 1 упаковку с 3 штуками товара. Максимальная прибыль составит 12.5 руб.
2.2.2. Простейшая задача управления запасами.
Модель, к изучению которой мы приступаем, играет такую же - или почти такую же - роль в исследовании операций, как законы Ньютона в физике. Хотя рассматриваемая ситуация и является идеализированной, в модели все же учитывается множество важных факторов, влияющих на выбор правил управления запасами.
Важно отметить, что внедрение модификаций рассматриваемой модели рядом промышленных фирм дало заметный экономический эффект. Разумеется, в таких случаях все необходимые вычислительные операции выполнялись на ЭВМ.
Рассмотрим задачу управления запасами на следующем примере.
Пример фирмы “Надежный поставщик”. Фирма должна разработать календарную программу выпуска некоторого вида изделий (или поставки некоторого вида товаров ) на плановый период, состоящий из 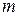 отрезков. Предполагается, что для каждого из этих отрезков имеется точный прогноз спроса на выпускаемую продукцию.
отрезков. Предполагается, что для каждого из этих отрезков имеется точный прогноз спроса на выпускаемую продукцию.
Для разных отрезков спрос неодинаков; кроме того, на экономические показатели влияет размер изготовляемых партий (размер закупки, учитывая кредит). Поэтому фирме нередко бывает выгодно изготавливать (закупать) в течение некоторого периода продукцию в объеме, превышающем спрос в пределах этого периода, и хранить излишки, для удовлетворения последующего спроса. Вместе с тем хранение возникающих при этом запасов связано с определенными затратами (проценты по кредитам).
Цель фирмы “Надежный поставщик” - разработать такую программу, при которой общая сумма затрат на производство (закупку) и на содержание запасов (проценты на кредит) минимизируются при условии полного и своевременного удовлетворения спроса на продукцию (что означает получение максимальной прибыли при наличии постоянных покупателей).
Анализ этой задачи начнем с преобразования качественного ее описания в математическую модель.
Построение модели.Введем переменные:
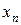 - выпуск продукции в течение отрезка
- выпуск продукции в течение отрезка 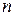 ;
;
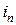 - уровень запасов на конец отрезка
- уровень запасов на конец отрезка 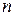 ;
;
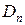 - спрос на продукцию на отрезке
- спрос на продукцию на отрезке 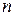 , предполагается, что величины спроса для всех
, предполагается, что величины спроса для всех 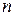 известны и являются неотрицательными целыми числами;
известны и являются неотрицательными целыми числами;
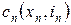 - затраты для отрезка
- затраты для отрезка 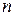 , которые зависят от уровня выпуска, запасов и длины интервала.
, которые зависят от уровня выпуска, запасов и длины интервала.
Тогда целевую функцию можно записать в следующем виде
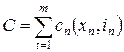 . .
| (2.15) |
На переменные 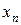 и
и 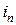 наложены несколько ограничений.
наложены несколько ограничений.
Во-первых, предполагается целочисленность объемов выпуска:
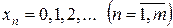 . .
| (2.16) |
Во-вторых, предполагается, что для администрации фирмы желателен нулевой уровень запасов на конец отрезка 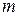 :
:
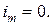
| (2.17) |
В-третьих, ставится условие полного и своевременного удовлетворения спроса в пределах каждого периода. Выполнение этого условия можно выполнить, вводя два ограничения. Первое из них назовем балансовым:
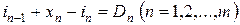 , ,
| (2.18) |
где 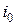 - заданный уровень запасов на начало планового периода.
- заданный уровень запасов на начало планового периода.
Второе ограничение заключается в том, чтобы уровень запасов на начало каждого периода и объем выпуска продукции должны быть достаточно велики, чтобы уровень запасов на конец периода был бы неотрицательным
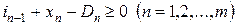 . .
| (2.19) |
Для того чтобы решить задачу при нелинейности каждой из величин 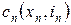 , сформулируем ее в терминах динамического программирования.
, сформулируем ее в терминах динамического программирования.
Динамическая постановка. Вспомним, что в задаче о загрузке мы строили вычислительный процесс от конечного состояния к исходному. Такой же подход будет использован и в настоящей задаче. Здесь конечным состоянием будет начало последнего отрезка планового периода, а исходным - начальный момент первого отрезка.
Применим следующие обозначения:
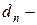 спрос на продукцию на отрезке
спрос на продукцию на отрезке 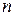 , отстоящем от конца планового периода (включая рассматриваемый);
, отстоящем от конца планового периода (включая рассматриваемый);
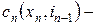 затраты на отрезке
затраты на отрезке 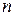 , связанные с выпуском
, связанные с выпуском 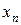 продукции и с содержанием запасов, уровень которых на конец отрезка равен
продукции и с содержанием запасов, уровень которых на конец отрезка равен 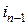 единиц. Для принятия решения об объеме выпуска не нужно знать, каким образом достигнут начальный уровень запасов.
единиц. Для принятия решения об объеме выпуска не нужно знать, каким образом достигнут начальный уровень запасов.
Для математической формулировки задачи введем следующие обозначения:
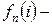 стоимость, отвечающая стратегии минимальных затрат на
стоимость, отвечающая стратегии минимальных затрат на 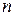 оставшихся отрезков при начальном уровне запасов
оставшихся отрезков при начальном уровне запасов 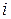 ;
;
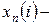 выпуск, обеспечивающий достижение
выпуск, обеспечивающий достижение 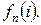
Согласно (2.17), уровень запасов на конец планового периода равен нулю, поэтому можно записать, что
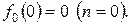
| (2.20) |
Затем перейдем к 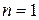 . Начальный уровень запасов
. Начальный уровень запасов 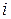 может определяться любым неотрицательным числом, не большим чем
может определяться любым неотрицательным числом, не большим чем 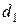 ; вне зависимости от значения
; вне зависимости от значения 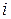 для полного удовлетворения потребности в пределах последнего отрезка объем выпуска должен быть равен
для полного удовлетворения потребности в пределах последнего отрезка объем выпуска должен быть равен 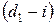 . Следовательно,
. Следовательно,
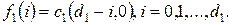
| (2.21) |
Перейдем к 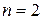 . Заметим, что если начальный уровень запасов равен
. Заметим, что если начальный уровень запасов равен 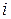 , а объем выпуска равен
, а объем выпуска равен 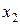 , то общие затраты для двух месяцев составляют
, то общие затраты для двух месяцев составляют
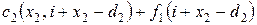 . .
| (2.22) |
причем предполагается, что выбранная стратегия для 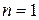 была оптимальной. Заметим, что величина
была оптимальной. Заметим, что величина 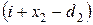 есть попросту уровень запасов на конец отрезка 2. Величина
есть попросту уровень запасов на конец отрезка 2. Величина 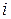 может принимать любые неотрицательные целочисленные значения не превышающие
может принимать любые неотрицательные целочисленные значения не превышающие 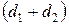 . (Вопрос к студентам: почему?). При заданном
. (Вопрос к студентам: почему?). При заданном 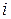 целочисленное значение
целочисленное значение 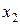 должно быть не меньше, чем
должно быть не меньше, чем 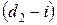 , что обеспечивает полное удовлетворение потребности на отрезке 2, но не больше чем
, что обеспечивает полное удовлетворение потребности на отрезке 2, но не больше чем 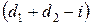 , так как конечный запас равен нулю. Оптимальному значению выпуска соответствует такое значение
, так как конечный запас равен нулю. Оптимальному значению выпуска соответствует такое значение 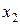 , при котором минимизируется сумма (2.22). Это можно выразить следующим общим выражением:
, при котором минимизируется сумма (2.22). Это можно выразить следующим общим выражением:
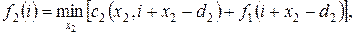
где 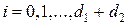 , причем для отыскания минимума перебираются все неотрицательные целые значения
, причем для отыскания минимума перебираются все неотрицательные целые значения 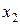 , заключенные в пределах
, заключенные в пределах 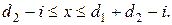
Очевидно, значения 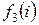 можно вычислить, если известны значения
можно вычислить, если известны значения 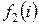 , и так далее. В конце концов, в данной задаче можно вычислить
, и так далее. В конце концов, в данной задаче можно вычислить 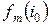 , где
, где 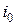 - уровень запасов на начало планового периода. Общее рекуррентное соотношение для любого периода теперь можно записать в следующем виде:
- уровень запасов на начало планового периода. Общее рекуррентное соотношение для любого периода теперь можно записать в следующем виде:
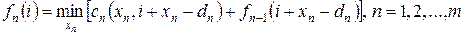 , ,
| (2.23) |
где 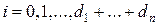 , причем для отыскания минимума перебираются все неотрицательные целые значения
, причем для отыскания минимума перебираются все неотрицательные целые значения 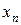 , заключенные в пределах
, заключенные в пределах 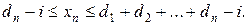
Заметим, что, поскольку начальный уровень запасов 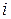 рассматривается как переменная величина, единственной независимой управляющей переменной в рекуррентном соотношении (2.23) является
рассматривается как переменная величина, единственной независимой управляющей переменной в рекуррентном соотношении (2.23) является 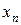 , так как уровень запасов на конец отрезка равен
, так как уровень запасов на конец отрезка равен 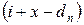 . Заметим также, что поскольку
. Заметим также, что поскольку 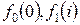 без труда вычисляются по формулам (2.20) и (2.21), то можно непосредственно и поочередно вычислить значения
без труда вычисляются по формулам (2.20) и (2.21), то можно непосредственно и поочередно вычислить значения 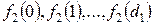 , а затем
, а затем 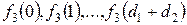 . Последовательно переходя ко все большим значениям
. Последовательно переходя ко все большим значениям 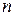 , мы дойдем до вычисления
, мы дойдем до вычисления 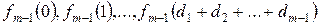 и, наконец, до
и, наконец, до 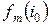 .
.
Процесс станет совершенно понятным, когда мы разберем пример, приводимый ниже.
Пример.Для упрощения будем считать, что спрос одинаков для всех отрезков планового периода. Для конкретности примем 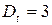 . Предположим также, что затраты равны сумме двух элементов: первый из них относится к производству, а второй определяется стоимостью содержания запасов и является линейной функцией от объема запасов. Таким образом, для всех отрезков
. Предположим также, что затраты равны сумме двух элементов: первый из них относится к производству, а второй определяется стоимостью содержания запасов и является линейной функцией от объема запасов. Таким образом, для всех отрезков
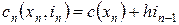 , ,
| (2.24) |
где
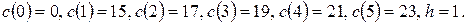
| (2.25) |
Далее, производственные мощности и складские площади фирмы (назовем ее “Надежный поставщик”) ограничены; это вводит в задачу дополнительное осложнение. Примем, что выпуск в течение одного отрезка не может превышать 5 единиц, а уровень запасов на конец отрезка - 4 единицы. Иными словами для всех отрезков
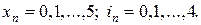
| (2.26) |
Решение.При наличии приведенных выше данных об условия деятельности фирмы “Надежный поставщик” можно составить динамическое рекуррентное соотношение, отображающее специфику задачи.
Для 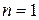
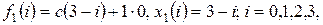
| (2.27) |
поскольку уровень запасов на конец планового периода равен нулю. В общем виде рекуррентное соотношение можно записать следующим образом:
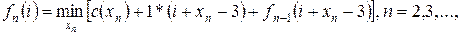
| (2.28) |
где 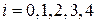 и для отыскания минимума перебираются все неотрицательные целые значения
и для отыскания минимума перебираются все неотрицательные целые значения 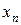 , заключенные в пределах
, заключенные в пределах 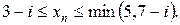 Ограниченность производственных мощностей, отображаемая первым из условий (2.26), не позволяет
Ограниченность производственных мощностей, отображаемая первым из условий (2.26), не позволяет 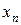 превысить 5, а ограниченность уровня запасов на конец отрезка, отображаемая второй частью (2.26), не позволяет
превысить 5, а ограниченность уровня запасов на конец отрезка, отображаемая второй частью (2.26), не позволяет 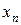 превысить
превысить 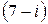 .
.
Для того чтобы анализ был содержательным, необходимо располагать всеми значениями функций 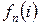 .
.
Для каждого шага 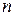 построена одна таблица; в ней предусмотрено по одной строке для каждого возможного значения начальных запасов
построена одна таблица; в ней предусмотрено по одной строке для каждого возможного значения начальных запасов 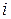 и по одному столбцу - для каждого возможного значения выпуска
и по одному столбцу - для каждого возможного значения выпуска 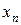 . Некоторые клетки в этих таблицах “запрещены” - они соответствуют недопустимым сочетаниям
. Некоторые клетки в этих таблицах “запрещены” - они соответствуют недопустимым сочетаниям 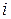 и
и 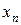 . Каждое из представленных в таблице чисел представляет собой сумму затрат для рассматриваемого отрезка
. Каждое из представленных в таблице чисел представляет собой сумму затрат для рассматриваемого отрезка 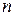 и оптимальных затрат для всех
и оптимальных затрат для всех 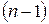 последующих отрезков. В двух правых столбцах таблицы представлены: минимальная по строке сумма (столбец
последующих отрезков. В двух правых столбцах таблицы представлены: минимальная по строке сумма (столбец 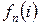 ) и соответствующий ей оптимальный выпуск (в столбце
) и соответствующий ей оптимальный выпуск (в столбце 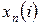 ).
).
Значения 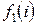 , вычисленные по формуле (2.27), приведены в таблице 6, а значения функции
, вычисленные по формуле (2.27), приведены в таблице 6, а значения функции 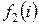 - в таблице 7.
- в таблице 7.
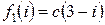
Таблица 6
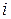
| 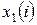
| 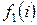
|
Дата добавления: 2020-11-18; просмотров: 765;











