Або кільцевого перерізу

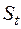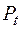Розрахункова схема вала редуктора, наведена на рис. 1.16 попереднього розділу, відповідає дійсності, якщо передача зусиль з ведених шківів здійснюється за допомогою сил тертя. У разі використання у точках О і Е навіть найпростіших зубчатих прямозубих коліс, окрім окружних компонентів зусиль та у зчепленні з’являються додаткові радіальні компоненти і 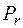. А якщо використати косозубі чи черв’ячні передачі, виникають ще й осьов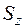і і . Величини радіальних та осьових зусиль є похідними від основних, окружних компонентів і залежать від геометричних параметрів зубчастих коліс [3]:

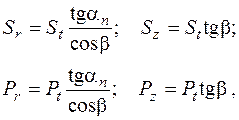(1.2.32)

де – кут головного профілю зуба (стандартне значення ),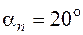

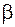– кут нахилу зуба до осі вала ( 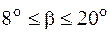), середнє значення якого становить .

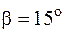При цьому окрім згинання в двох площинах 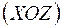та 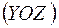в поперечному перерізі стержня виникає дія поздовжньої сили, що спричиняється осьовими зусиллями. Напруження від деформацій згинання та розтягання (стискання) діють по нормалі до поперечного перерізу. Отже, сумарне нормальне напруження можна визначити як алгебраїчну суму окремих компонентів від згинання та від розтягання (стискання) – .

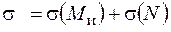Додатково, враховуючи дію кручення, маємо розподіл дотичних напружень від кручення. Якщо, як в попередньому розділі, нехтуємо дією поперечних зусиль в силу їх малості в круглому або кільцевому перерізі, то дотичне напруження можна визначити .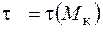

Напружений стан при цьому також буде двохвісним або плоским. Еквівалентні напруження, згідно з відповідною теорією міцності можуть бути записані:

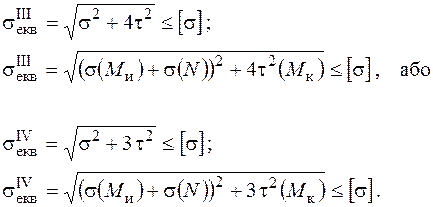(1.2.33)

Приклад 1.2

Як і в попередньому прикладі вал редуктора передає потужність 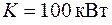, яка розподіляється між веденими шестернями у співвідношенні 1:3, і обертається з кутовою швидкістю 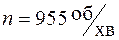. Допустиме напруження матеріалу вала .

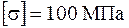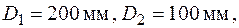
Розрахункова схема редуктора з косозубими веденими колесами наведена на рис. 1.19.

Додаткові зусилля з урахуванням (1.2.30), (1.2.32) дорівнюють

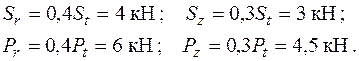
Як і у попередньому прикладі, зробимо приведення усіх діючих сил до центрів ваги валу у відповідних перерізах. Перед тим зазначимо, що зусилля, прикладені до валу редуктора (рис. 1.19), можна умовно розподілити на дві групи.

Перша включає ті, що потрапляють до заданих точок, рухаючись вздовж лінії власної дії. При такому просуванні сили ніякі додаткові моменти не утворюються. У нашому прикладі це радіальні зусилля і .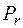

До другої групи належать ті сили, що можуть потрапити до центрів ваги валу тільки шляхом паралельного переносу. У цих випадках до перенесеної сили треба додати ще й момент, який утворюється у площині переносу. Остання визначається за двома напрямками: перший – той, у якому діє сила, другий – плече переносу (найкоротша відстань від лінії, вздовж якої діє сила, до заданої точки). Обертання утвореного моменту відносно осі, ортогональної до площини його дії, здійснюється в напрямку сили.

Рисунок 1.19

Так у точці О перенос сил відбувається за схемою, наданою на рис. 1.20.

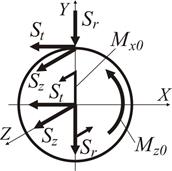
Рисунок 1.20

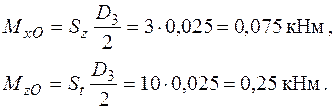
Розподіл силових факторів в точці Е наведений на рис. 1.21.

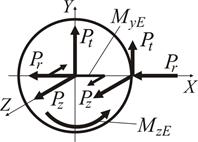Рисунок 1.21

Переніс зусиль 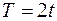та 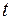до точки С здійснюється так само, як у попередньому прикладі (рис. 1.17). Загальна схема дії сил зображена на рис. 1.19.

Як і у попередньому розділі, розкладемо складне просторове навантаження на окремі прості, згідно з принципом суперпозиції. У даному випадку, окрім кручення і згинання у двох головних площинах валу, при наявності осьових компонентів 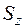та , з’являються додаткові навантаження розтягання і стискання.

Окружні зусилля 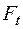, , залишаються ти самі, що і у попередньої задачі, тому зберігається і розподіл крутних моментів , , .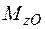

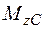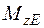Зміни у розрахункових схемах згинання, у порівнянні з попереднім прикладом, потребують перерахунків опорних реакцій та перебудови епюр згинальних моментів та .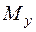

У площині :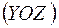

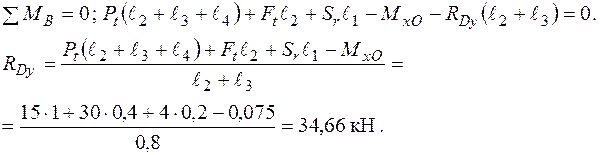
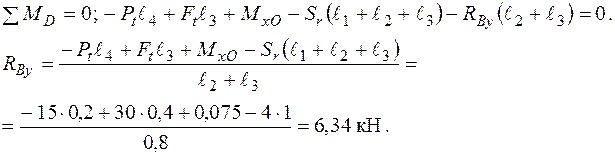
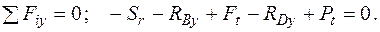
Згинальні моменти в перерізах вала підраховуються наступним чином:

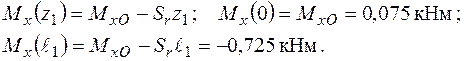
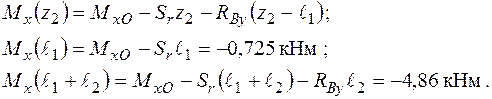
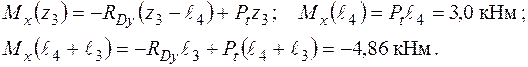
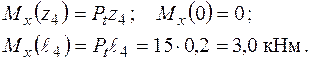
У площині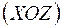

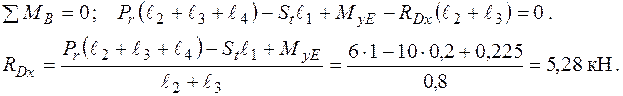
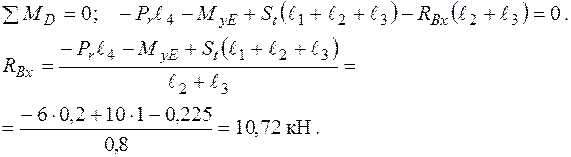
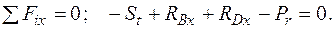
Згинальні моменти в перерізах вала підраховуються так:

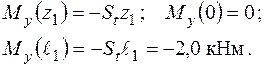
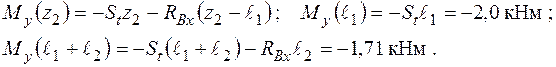
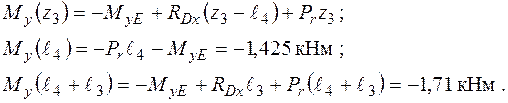
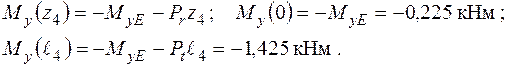
Схема дії розтягання − стискання та епюра поздовжніх сил 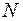наведена на рис. 1.19. Слід нагадати, що для побудови епюри спочатку треба урівноважити вал у поздовжньому напрямку, тобто виконати умову

.

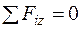Реактивне зусилля 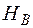виникає у точці, де встановлена нерухома у даному напрямку опора. З умов рівноваги 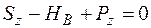дістаємо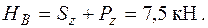

Враховуючи правила знаків для внутрішніх поздовжніх сил, маємо:

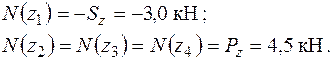
Для валів круглого поперечного перерізу умови міцності (1.2.33) набувають вигляду

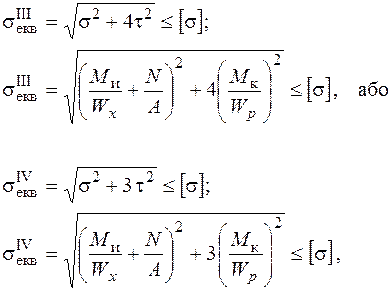(1.2.34)

де 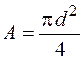, , 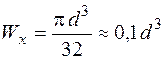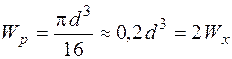– площа, осьовий та полярний моменти опору круглого перерізу відповідно.

Рівняння (1.2.34) можна використати і у разі кільцевого перерізу, для якого геометричні характеристики профілю мають вигляд:

, ,

,

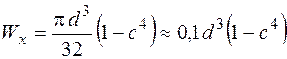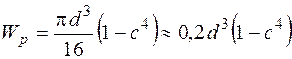де 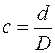– співвідношення між внутрішнім 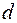та зовнішнім 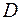діаметрами кільця.

Пошук небезпечного перерізу провадять за допомогою обчислення еквівалентних моментів (1.2.27), так само, як у попередньому розділі. Так у нашому прикладі, використовуючи ІV гіпотезу міцності знайдемо, що у перерізі С справа

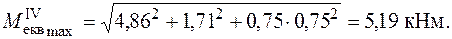
На відміну від прикладу 1.1 (див. рис. 1.14) положення найбільш напруженої точки залежить від знака поздовжньої сили. Якщо у перерізі діє розтягувальне зусилля 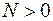, яке дає додатні напруження 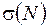, то найбільші небезпечною стає точка 1:

.

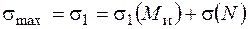У разі дії стискаючого зусилля 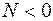найбільші напруження, за модулем, виникають у точці 2:

.

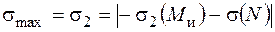Зважаючи на те, що для перерізів у вигляді кола та кільця

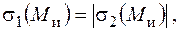
можна узагальнити умови міцності в найбільш небезпечній точці для будь-якої за знаком поздовжньої сили:

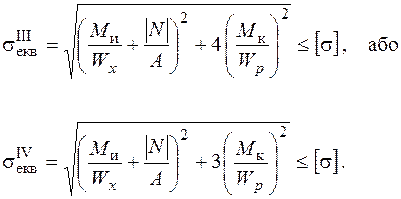(1.2.35)

Для спрощення розрахунків обчислення діаметру вала на першому етапі проводиться без урахування дії поздовжньої сили. При цьому початкове (занижене) значення діаметру визначається за формулою (1.2.31), яке на другому етапі розрахунків уточнюється за вимогами (1.2.35).

Отже, визначимо початкове (приблизне) значення діаметру вала:

.

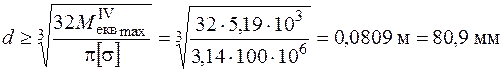Після округлення діаметру до найближчого стандартного значення маємо: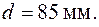

Проведемо уточнюючі підрахунки. Для цього за визначеним діаметром підрахуємо окремі складові напружень у виразі (1.2.35). З епюри поздовжньої сили визначаємо, що у перерізі С діє зусилля 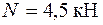. Тоді

.

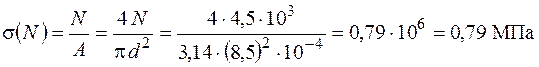Згинальний момент у перерізі С:

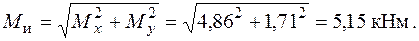
Напруження від згинання:

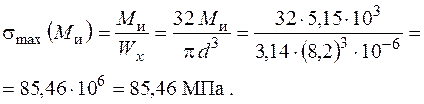
Сумарні нормальні напруження:

.

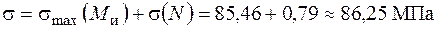Максимальні дотичні на контурі перерізу С від крутного моменту:

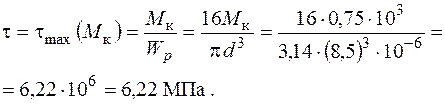
Тоді еквівалентні напруження дорівнюють

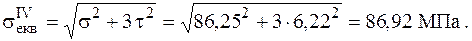
Знайдене еквівалентне напруження значно менше допустимого, тому з метою економії матеріалу беремо менше стандартне значення діаметру − 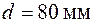та повторюємо перевірочний розрахунок.

.

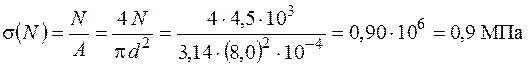Згинальний момент у перерізі С:

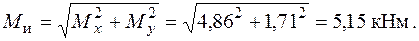
Напруження від згинання:

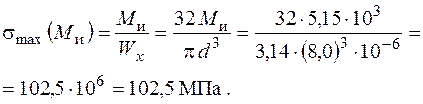
Сумарні нормальні напруження:

.

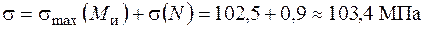Максимальні дотичні на контурі перерізу С від крутного моменту:

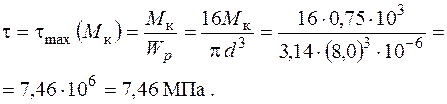
Тоді еквівалентні напруження дорівнюють

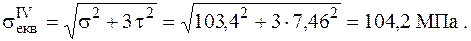
Знайдені еквівалентні напруження перевищують допустимі значення менш ніж на 5 відсотків, тому остаточно приймаємо діаметр .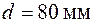

У разі дії значних поздовжніх зусиль, еквівалентні напруження можуть також перевищувати допустимі значення. Тоді слід прийняти наступне більше стандартне значення діаметру вала і повторити підрахунки .