Напруження при центральному розтяганні – стисканні
Розглянемо розтягання прямолінійного стержня довільного поперечного перерізу під дією двох рівних по величині та протилежно спрямованих сил (рис. 1.3 а). У довільному місці стержня уявно проведемо поперечний переріз, відкинемо праву частину, дію відкинутої частини на ту, що залишилася, замінимо внутрішнім зусиллям 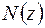 , що з рівняння статичної рівноваги
, що з рівняння статичної рівноваги 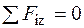 визначиться як
визначиться як 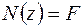 (рис. 1.3 б). Поздовжня сила
(рис. 1.3 б). Поздовжня сила 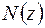 є рівнодіючою (результуючою) внутрішніх зусиль, які довільним образом розподілені по точках перерізу
є рівнодіючою (результуючою) внутрішніх зусиль, які довільним образом розподілені по точках перерізу 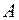 , та нормальні до нього. Тобто при центральному розтяганні - стисканні у поперечному перерізі виникає тількинормальне напруження
, та нормальні до нього. Тобто при центральному розтяганні - стисканні у поперечному перерізі виникає тількинормальне напруження 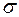 (рис. 1.3 в).
(рис. 1.3 в).
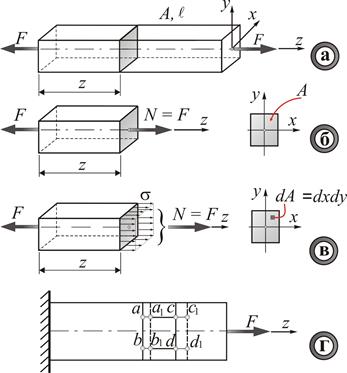
Рисунок 1.3
Очевидно, що на елементарну площадку 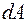 діє елементарна поздовжня сила
діє елементарна поздовжня сила 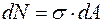 . Звідси одержуємо рівняння в інтегральному вигляді:
. Звідси одержуємо рівняння в інтегральному вигляді:
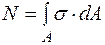 . (1.1)
. (1.1)
Вирішити це рівняння неможливо, тому що невідомий закон розподілу по перерізу напруження 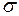 .
.
Щоб описати закон розподілу напружень 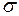 по поперечному перерізу, звернемося до досліду. Як показують експерименти, при центральному розтяганні – стисканні однакові подовжні відрізки
по поперечному перерізу, звернемося до досліду. Як показують експерименти, при центральному розтяганні – стисканні однакові подовжні відрізки 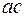 і
і 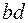 стержня одержують однакові подовження (рис. 1.3 г):
стержня одержують однакові подовження (рис. 1.3 г): 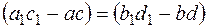 . Лінії на бічній поверхні стержня, що являють собою сліди поперечних перерізів, рівнобіжні до деформування, залишаються рівнобіжними й у процесі деформування: ab || a1b1 і cd || c1d1.
. Лінії на бічній поверхні стержня, що являють собою сліди поперечних перерізів, рівнобіжні до деформування, залишаються рівнобіжними й у процесі деформування: ab || a1b1 і cd || c1d1.
Це дозволяє вважати, що при центральному розтяганні – стисканні виконується гіпотеза плоских перерізів: переріз плоский та нормальний до осі (поперечний переріз) до деформації залишається плоским та нормальним до осі в процесі деформації, тобто переміщуючись, переріз залишається паралельним (рівнобіжним) самому собі. Якщо уявити модель стержня, що складається з окремих подовжніх волокон, то при розтяганні кожне волокно подовжується на одну і ту ж величину. Отже, у кожному подовжньому волокні діє однакове зусилля. Цей висновок дозволяє вважати, що при центральному розтяганні − стисканні нормальне напруження 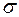 по поперечному перерізу розподіляється рівномірно, тобто
по поперечному перерізу розподіляється рівномірно, тобто 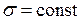 .
.
Тоді з рівняння (1.1) маємо: 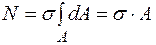 , звідси нормальне напруження для всіх точок перерізу при центральному розтяганні – стисканні буде однаковим, і визначиться формулою
, звідси нормальне напруження для всіх точок перерізу при центральному розтяганні – стисканні буде однаковим, і визначиться формулою
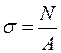 . (1.2)
. (1.2)
У розглянутому випадку напруження 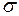 залишаються постійними як по перерізу, так і по довжині(якщо повздовжня сила та площа поперечного перерізу постійні), тобто по всьому обсягу стержня. Такий напружений стан називається однорідним.
залишаються постійними як по перерізу, так і по довжині(якщо повздовжня сила та площа поперечного перерізу постійні), тобто по всьому обсягу стержня. Такий напружений стан називається однорідним.
Максимальні розрахункові нормальні напруження, обчислені за формулою (1.2), повинні зіставлятися з гранично допустимими напруженнями для матеріалу стержня, що забезпечують безпечну експлуатацію. Ці напруження називаютьсядопустимими напруженнями 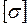 .
.
Сформулюємо умову міцності при центральному розтяганні – стисканні, яка повинна виконуватись в кожній точці поперечних перерізів даного стержня:
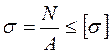 . (1.3)
. (1.3)
Для матеріалів, що мають неоднакові характеристики при розтяганні та стисканні, умова міцності (1.3) набуває вигляд:
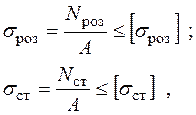 (1.4)
(1.4)
де 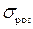 та
та 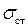 – найбільші нормальні напруження при розтяганні та стисканні відповідно.
– найбільші нормальні напруження при розтяганні та стисканні відповідно.
Переріз стержня, у якому виникає найбільше нормальне напруження, є небезпечним.
Напруження, що допускається (допустиме напруження) , визначається як небезпечне напруження для даного матеріалу 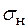 , поділене на нормативний коефіцієнт запасу
, поділене на нормативний коефіцієнт запасу 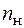 , тобто
, тобто 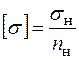 . Для пластичних матеріалів за небезпечне напруження приймається границя текучості
. Для пластичних матеріалів за небезпечне напруження приймається границя текучості 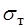 , а для крихких – тимчасовий опір
, а для крихких – тимчасовий опір 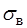 .
.
Дата добавления: 2020-10-14; просмотров: 665;











