Режимы при больших возмущениях и больших изменениях скорости (расчеты асинхронного хода, ресинхронизации, результирующей устойчивости).

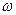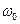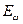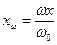Для асинхронного режима характерно пе­риодическое изменение вектора эдс хотя бы одной станции системы на угол, больший 360°, вследствие того что роторы генераторов вра­щаются со скоростью , отличной от синхрон­ной . При этом синхронная машина одно­временно с синхронным развивает и асинхрон­ный момент, а ее параметры, зависящие от скольжения, приобретают новые значения ( и ). В этих условиях ток, циркулирующий в элементах системы, имеет слагаю­щие двух частот: 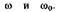Асинхронные двигатели нагрузки, реагируя на изменение частоты и напряжения, будут изменять свои мощности и скорость. При значительных отклонениях частоты в системе индуктивные и емкостные сопротивления трансформаторов, линий и других неподвижных элементов будут также претерпевать изменения. Следовательно, расчет асинхронных режимов систем, строго говоря, должен выполняться в условиях, когда ряд элементов учитывается специфическими для них параметрами и характеристиками.

Так, отдаваемая синхронными машинами мощность в генераторном режиме и получа­емая в двигательном режиме зависят не толь­ко от угла, но и от скорости его изменения. В этом случае упрощенно можно предпо­ложить, что мощность Р и электромагнитный момент М будут иметь составляющие — синхронную и асинхронную, т. е.

; ,

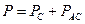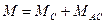при этом

; .

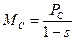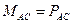Синхронная мощность определяется .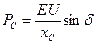

Асинхронная мощность определяется:

,

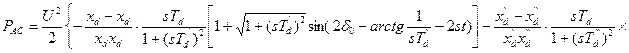
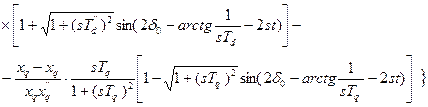где 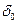- угол начала отсчета.

Среднее значение асинхронной мощности

.

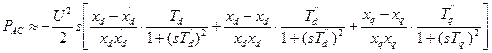Полная реактивная мощность (синхронная, асинхронная и намагничивания):

.

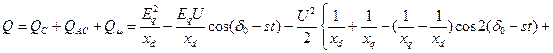
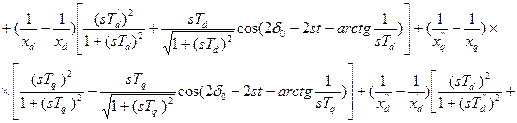
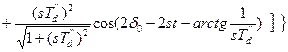Приведенные выражения справедливы при связи генератора с шинами неизменного напря­жения через сопротивление 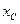, которое введено в сопротивления 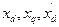и др. Их можно применять для приближенных расчетов, когда система представлена эквивалентным генера­тором с эдс 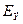и сопротивлениями .

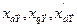При определении допустимости в энергосистеме режима, связанного с асинхронным ходом, проверяют:

1) для машин, работающих асинхронно,— механические усилия, которые они будут испытывать, допустимую длительность по нагреву ротора и статора при максимально возмож­ном скольжении;

2) характер асинхронного хода после на­рушения синхронизма (устойчивый, неустой­чивый, перемежающийся синхронно-асинхрон­ный) и условия синхронизации;

3) допустимость асинхронного хода по условиям режима части системы, сохранившей
нормальную синхронную работу. Для этого в ней определяют: распределение мощностей,
напряжение в контрольных узловых точках; возможность появления лавины напряжения
при его глубоких посадках; изменение частоты; возможность неправильного действия релейной
защиты и системной автоматики.

Основная цель всех расчетов — оценка возможного скольжения машины, работающей асинхронно, и общей длительности асинхрон­ного хода и больших качаний.

Особенности и порядок расчета результи­рующей устойчивости. Математическое описа­ние процессов может быть основано на использовании либо дифференциальных урав­нений, связывающих мгновенные значения пе­ременных (уравнения Парка — Горева), либо дифференциальных и алгебраических уравнений, рас­сматривающих огибающие мгновенных зна­чений переменных. В каждом из этих случаев параметры расчетной схемы могут прини­маться постоянными или переменными, зави­сящими от частоты.

Первый этап решения системы уравнений, описывающей процесс с той или иной сте­пенью идеализации, заключается в определении потокораспределения (токораспределения) и скольжения генераторов, работающих асин­хронно, проводимый в предположении задан­ного напряжения (по действующему значению и частоте) в одной из точек системы. На втором этапе выявляют возможность ресин­хронизации части энергосистемы, работающей асинхрон­но. Оба этапа расчета ведутся методом после­довательных приближений.