Исследование относительного движения ротора с помощью способа площадей.
При малых изменениях частоты вращения с небольшой погрешностью (1 — 1,5%) можно прини- мать 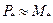 . Основное уравнение движенияротора в относительных единицах
. Основное уравнение движенияротора в относительных единицах
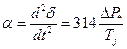
где 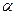 - угловое электрическое ускорение, рад/с2;
- угловое электрическое ускорение, рад/с2;
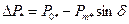 — избыточная мощность;
— избыточная мощность;
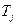 — постоянная инерция агрегата, с.
— постоянная инерция агрегата, с.
Способ площадей позволяет определить размах колебаний ротора при отклонениях его от положения равновесия и найти тот предельный угол отключения аварийного участка системы, при котором устойчивая работа может быть сохранена. Предельный угол отключения, найденный из условия равенства площадок ускорения и торможения в простейшей энергосистеме: схема станция — шины (рис. 2.16), определяется выражением, пригодным при любых видах кз:
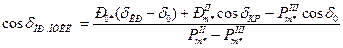 ,
,
где 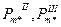 — максимальные значения мощностей, определенные соответственно по характеристикам послеаварийного и аварийного режимов;
— максимальные значения мощностей, определенные соответственно по характеристикам послеаварийного и аварийного режимов;
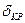 — критический угол (электрический), рад.
— критический угол (электрический), рад.
При определении 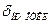 трехфазного кз вблизи шин передающей электростанции
трехфазного кз вблизи шин передающей электростанции 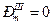 .
.
Способ площадей может быть применен:
- для исследования системы, состоящей из двух станций, работающих параллельно на общие нагрузки;
- для определения мощности нагрузки, которую необходимо отключить, чтобы обеспечить устойчивость параллельной работы при отключении части генераторов в системе;
- для анализа эффективности форсирования возбуждения и регулирования мощности турбин с целью улучшения динамической устойчивости и т.д.
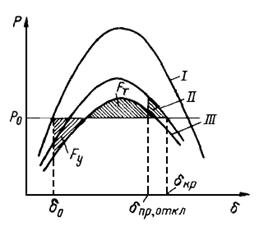
Рис. 2.16. Характеристики мощности: I – нормального режима; II – послеаварийного режима; III – аварийного режима; Fт – площадка торможения; Fу – площадка ускорения
Способ площадей не дает возможности получить зависимость изменения угла во времени. Для определения ее необходимо решить основное дифференциальное уравнение движения ротора, т. е. найти  =f(t). Аналитическое выражение зависимости
=f(t). Аналитическое выражение зависимости  =f(t) путем интегрирования уравнения движения можно получить только в некоторых частных случаях. Так, в схеме станция — шины, проинтегрировав уравнение движения, получим:
=f(t) путем интегрирования уравнения движения можно получить только в некоторых частных случаях. Так, в схеме станция — шины, проинтегрировав уравнение движения, получим:
1) при 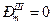 — трехфазное кз у шин генератора или отключение всех генераторов от сети:
— трехфазное кз у шин генератора или отключение всех генераторов от сети:
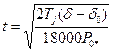 ;
;
2) при Ро = 0 — исчезновение момента сопротивления у синхронного двигателя, подключенного к сети:
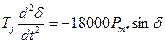 ;
;
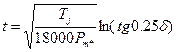 .
.
Общим методом решения дифференциального уравнения относительного движения ротора является метод численного интегрирования при его простейшей модификации, именуемой методом последовательных интервалов. Для более точных расчетов применяют метод Рунге — Кутта или метод Штермера, предусматривающие поправки на устранение погрешностей.
При решении задачи методом последовательных интервалов весь процесс изменения угла во времени разбивают на интервалы 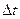 , предполагая, что в течение каждого интервала
, предполагая, что в течение каждого интервала 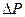 остается неизменным.
остается неизменным.
Выражения для приращения угла в первом и последующих интервалах:
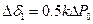 ;
;
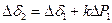 ;
;
……………………
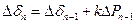 .
.
Здесь 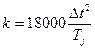 , где время
, где время 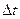 и постоянная
и постоянная 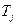 выражены в секундах, а электрический угол
выражены в секундах, а электрический угол 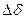 — в градусах.
— в градусах.
По приращениям угла во времени строится зависимость 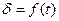 .Значение
.Значение 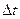 принимается обычно равным 0,02 – 0,1 с.
принимается обычно равным 0,02 – 0,1 с.
Если на каком-то интервале п режим изменяется скачком (отключается поврежденная линия или часть генераторов), т. е. избыток мощности, составляющий 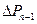 внезапно становится равным
внезапно становится равным 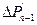 , то приращение угла в этом интервале определяется как6
, то приращение угла в этом интервале определяется как6
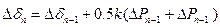 .
.
Формально изменение режима отражается здесь изменением собственных и взаимных проводимостей, по новым значениям которых определяется 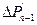 .
.
Этот общий метод решения уравнений применим для систем любой сложности. При этом об устойчивости энергосистемы судят по изменению не абсолютных, а относительных углов
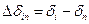 , где i=l, 2, ..., п- 1.
, где i=l, 2, ..., п- 1.
Использование типовых кривых для определения зависимости  =f(t). Уравнение относительного движения ротора можно представить в обобщенном виде
=f(t). Уравнение относительного движения ротора можно представить в обобщенном виде
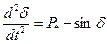 ,
,
где
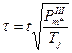 и
и 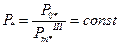 .
.
Уравнение содержит три обобщенных параметра: 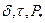 .По этому уравнению можно построить типовые универсальные зависимости
.По этому уравнению можно построить типовые универсальные зависимости 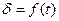 при заданных
при заданных 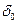 и
и 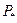 . При известных предельном угле отключения
. При известных предельном угле отключения 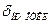 и
и 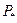 по типовым зависимостям определяют предельное время отключения в условных единицах
по типовым зависимостям определяют предельное время отключения в условных единицах 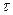 , отвечающее ему время в секундах будет:
, отвечающее ему время в секундах будет:
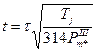 .
.
Дата добавления: 2020-10-14; просмотров: 624;











