Анализ нерегулируемой системы из двух станций.
Дифференциальное уравнение системы
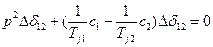 ,
,
где 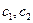 находятся дифференцированием выражения для мощности первой и второй станций по углу
находятся дифференцированием выражения для мощности первой и второй станций по углу 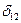 .
.
Корни характеристического уравнения
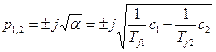
дают возможность установить, что устойчивость не нарушается при положительном значении относительного ускорения 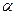 .
.
При учете нагрузки статическими характеристиками мощности 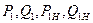 находят из выражений:
находят из выражений:
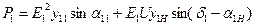 ;
;
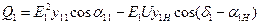 ;
;
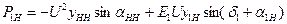 ;
;
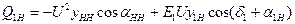 ,
,
где 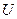 - напряжение в точке включения нагрузки;
- напряжение в точке включения нагрузки;
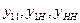 - собственные и взаимные проводимости ветвей источника и нагрузки.
- собственные и взаимные проводимости ветвей источника и нагрузки.
Уравнения второй станции можно получить, заменив в первых двух уравнениях индекс 1 на индекс 2.
Рис.2.17 Схема системы с двумя станциями, работающими на общую нагрузку.
Для определения 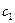 и
и 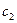 пользуются выражениями:
пользуются выражениями:
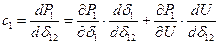 ;
;
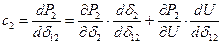 .
.
Частные производные 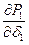 ;
; 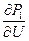 ;
; 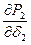 ;
; 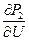 находятся дифференцированием уравнений для мощностей после подстановки в них численных значений:
находятся дифференцированием уравнений для мощностей после подстановки в них численных значений:
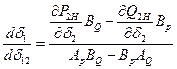 ;
;
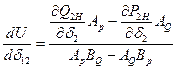 ,
,
где 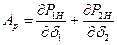 ;
;
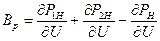 ;
;
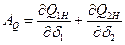
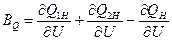 ,
,
причём 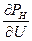 и
и 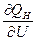 принимаются по статическим характеристикам нагрузок для данного напряжения
принимаются по статическим характеристикам нагрузок для данного напряжения 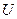 .
.
Производная 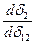 определяется из уравнения
определяется из уравнения
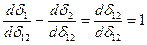 .
.
Подстановка производных 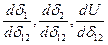 в выражения для
в выражения для 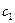 и
и 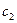 позволяет вычислить их и найти относительное ускорение
позволяет вычислить их и найти относительное ускорение 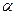 .
.
Дата добавления: 2020-10-14; просмотров: 850;











