Понятие о статической устойчивости.

Врассматриваемых простейших условиях признаком устойчивости системы является такой характер изменения мощностей и моментов при небольшом отклонении от состояния равновесия, который вынуждает систему вновь возвращаться к исходному состоянию. В режиме работы в точке а (рис.2.9), мощности генератора и турбины уравновешивают друг друга. Если допус­тить, что угол 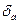получает небольшое приращение 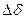, то мощность гене­ратора, следуя синусоидальной зависимости от угла, также изменится на некоторую величину 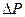, причем, как вытекает из рис.2.9, в точке а поло­жительному приращению угла 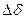соответствует также положительное изме­нение мощности генератора 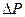. Что же касается мощности турбины, то она не зависит от угла и при любых изменениях последнего остается посто­янной и равной Р_о. 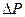В результате изменения мощности генератора равно­весие моментов турбины и генератора оказывается нарушенным и на валу машины возникает избыточный момент тормозящего характера, поскольку тормозящий момент генератора в силу положительного изменения мощности преобладает над вращающим моментом турбины.

Под влиянием тормозящего момента ротор генератора начинает замед­ляться, что обусловливает перемещение связанного с ротором вектора эдс генератора 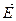в сторону уменьшения угла .

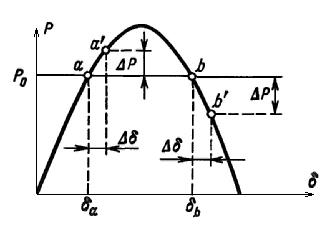
Рис.2.9 Изменение мощности при приращениях угла.

результате уменьшения угла вновь вос­станавливается исходный режим работы в точке а и, следовательно, этот режим должен быть признан устойчивым. К тому же выводу можно прийти и при отрица­тельном приращении угла 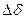в точке а.

Совершенно иной получается картина в точке 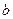. Здесь положительное прираще­ние угла 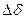сопровождается не положи­тельным, а отрицательным изменением мощности генератора 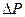. Изменение мощ­ности генератора вызывает появление избы­точного момента ускоряющего характера, под влиянием которого угол не умень­шается, а возрастает. С ростом угла мощ­ность генератора продолжает падать, что обусловливает дальнейшее увеличение угла и т. д. Процесс сопровождается непрерывным перемещением вектора эдс 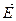относительно вектора напря­жения приемной системы U и станция выпадает из синхронизма. Таким образом, режим работы в точке 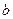статически неустойчив и практи­чески неосуществим.

Под статической устойчивостью, вообще говоря, понимают способность системы самостоятельно восстановить исходный режим работы при малом возмущении. Статическая устойчивость является необходимым условием существования установившегося режима работы системы, но отнюдь не предопределяет способности системы продолжать работу при резких наруше­ниях режима, например, при коротких замыканиях. Эта сторона проблемы, так называемая динамическая устойчивость системы, будет исследована ниже.

Итак, точка а и любая другая точка на возрастающей части синусои­дальной характеристики мощности отвечают статически устойчивым режи­мам и, наоборот, все точки падающей части характеристики — статически неустойчивым. Из приведенных выше соображений, характеризующих усло­вия работы системы, непосредственно вытекает следующий формальный
признак статической устойчивости рассмотренной простейшей системы: при­ращения угла и мощности генератора Р должны иметь один и тот же знак, т. е. 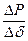> 0 или, переходя к пределу, 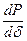> 0.

Производная 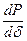, как известно, носит название синхронизирующей мощ­ности, и, следовательно, критерием статической устойчивости системы в рас­смотренных условиях является положительный знак синхронизирующей мощ­ности. Производная мощности по углу равна

;

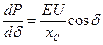она положительна при < 90° (рис.2.10). В этой области и возможны устойчивые установившиеся режимы работы системы. Критическим с точки зрения устойчивости в рассматриваемых условиях (при чисто индуктивной связи генератора с шинами приемной системы) является значение угла = 90°, когда достигается максимум характеристики мощности.

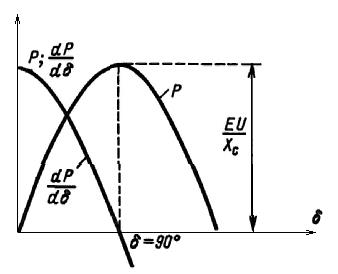
Рис.2.10 Зависимость синхронизирующей мощности от угла.