Уравнения Парка – Горева для синхронной машины.

Уравнения Парка — Горева связывают между собой мгновенные значения токов, магнитных пото­ков, напряжений в осях координат (d, q), связанных с ротором.

Мгновенные значения параметров режима опре­деляют как проекции на оси времени фаз а, b, с вектора тока (напряжения, ЭДС, потокосцепления), вращающегося с угловой ско­ростью 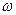. Этот вектор тока называют обобщенным.

Оси времени t_a, t_b, t_c фаз a, b, с неподвижны и совпадают с осями обмоток статора (рис. 2.1). Мгновенные значения фазных токов равны:

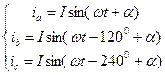
где 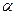— произвольный угол.

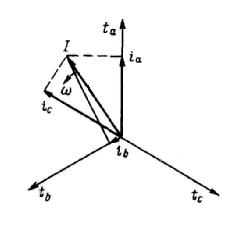
Рис.2.1 Обобщенный вектор тока 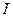и его проекции на временные оси.

Проекции обобщенного вектора тока на оси d, q, связанные с ротором, дают значения продольного и поперечного токов (рис. 2.2):

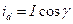
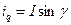
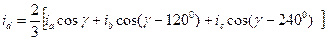
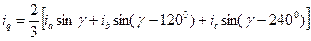
При наличии токов нулевой последовательности

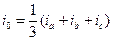
Соотношения, аналогичные приведенным выше, справедливы для напряжений, ЭДС и потокосцеплений.

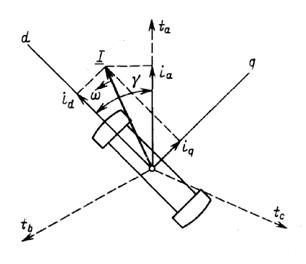
Рис. 2.2. Обобщенный вектор тока I и проекции его

на продольную и поперечную оси ротора

Связь между мгновенными значениями фазных величин и величин в продольной и поперечной осях устанавливается на основе уравнений:

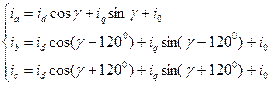
Угол 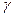меняется во времени:

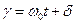
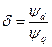
где 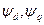— полное потокосцепление статора в продольной и поперечной осях.

В случаях симметричного режима энергосистемы токи нулевой последовательности отсутствуют ( 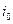= 0).

Значения потокосцепления статора в поперечной и продольных осях определяются из вы­ражений:

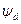= G (р) U_f + X_d (р) i_d

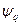= X_q (p) ,

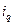где G(p)—операторная проводимость маши­ны;

X_d(p), X_q(p) — операторные сопротивления машины в продольной и поперечной осях;

U_f — напряжение возбуждения машины.

Для машины без демпферных обмоток и эквивалентных им контуров:

;

;

.

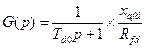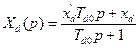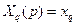Если известна ЭДС 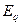, то

,

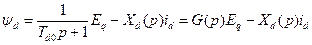где 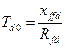- постоянная времени обмотки возбуждения машины при разомкнутой обмотке статора;

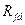- активное сопротивление обмотки статора по продольной оси;

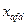- реактивное сопротивление взаимной индукции обмотки возбуждения со статором в продольной оси;

- реактивное сопротивление индуктивности ротора в продольной оси.

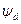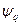Для машины с демпферными обмотками значения потокосцепления статора в поперечной и продольных осях и определяются теми же уравнениями.

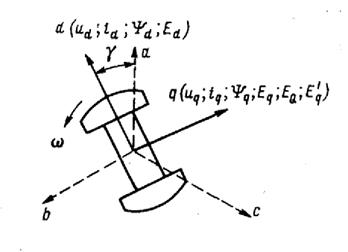
Рис.2.3 Основные параметры синхронной машины для принятых направлений осей.

Уравнения Парка – Горева для принятых на рис.2.3. направлениях осей примут вид:

;

;

;

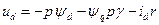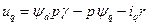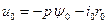где 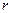- активное сопротивление статора;

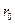- активное сопротивление статора нулевой последовательности;

; ;

.

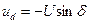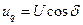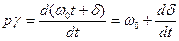В системе относительных единиц 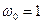, поэтому .

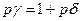Третье уравнение системы относится к слу­чаю несимметричного режима или несиммет­ричной схемы.

Уравнения, приведенные выше, полностью описывают переходный процесс машины, ра­ботающей на шины неизменного напряжения. Для анализа переходного процесса в сложной энергосистеме уравнения составляются для каждого эле­мента (генераторов, нагрузок, участков сети) и решаются совместно.

Решение системы урав­нений Парка – Горева относительно токов или других величин, рассматриваемых как неизвестные, проводится в операторной форме (для изобра­жений), например находятся значения токов

; ;

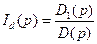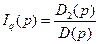где 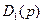, D₂ (p) — миноры определителя систе­мы; D (р) — главный определитель системы.

Характер переходного процесса в системе определяется знаком действительной части корней определителя D(р). При Re(p_t, ... ..., р_n) < 0 переходный процесс затухающий.

Если изменения напряжений U_d, U_q, U_f заданы, то

.

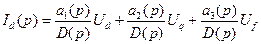
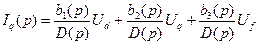Токи как функции времени находят, переходя от изображений к оригиналам, что может быть сделано с помощью формулы разложения.

Момент электромагнитных сил, действующих на ротор во время его относительного вращения, определяется суммой моментов, действующих по поперечной и продольной осям:

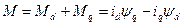
Мощность на шинах машины:

,

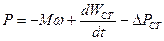где 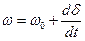- частота вращения ротора;

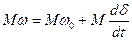- электромагнитная мощность, передаваемая с ротора на статор;

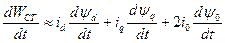- дополнительная мощность, соответствующая изменению электромагнитной энергии, запасённой в индуктивности машины;

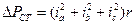- потери в активном сопротивлении статора.

Вращающий момент, приложенный к валу генератора, М_мех должен уравновешивать мо­мент, связанный с электрической мощностью, отдаваемой в сеть Р_ЭЛ и расходуемой на потери в статоре 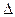Р_СТ; появление мощности dW_CT/dt может вызвать дополнительный вра­щающий момент, тормозящий (при коротком замыкании) или ускоряющий (при отключении его) ротор, поэтому

,

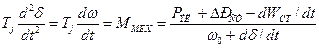где 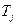- постоянная инерции машины.

Для определения параметров при переходных процессах можно использовать упрощенные уравнения Парка – Горева. Для получения этих уравнений отказы­ваются от учета влияния:

1) апериодической составляющей тока ста­тора (трансформаторной ЭДС);

2) периодических токов ротора, связанных с апериодическими составляющими тока ста­тора;

3) активного сопротивления в цепи ста­тора.

В системе относительных единиц при 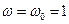уравнения Парка - Горева для синхронной машины будут иметь вид:

; .

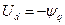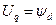Данные уравнения положены в основу рас­четов периодической составляющей токов короткого замыкания при обычно принимаемых допущениях.

При принятых предпосылках отдаваемая мощность численно равна вращающемуся моменту; поэтому для симметричного режима или режима, условно приведённого к симметричному,

.

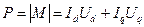Уравнение относительного движения ротора

.

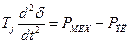На основе этих расчетных уравнений (их иногда называют уравнениями Лонглея или уравнениями Лебедева — Жданова) обычно ведутся проектные и эксплуатацион­ные расчеты устойчивости. Они позволяют для расчетов переходных процессов пользоваться соотношениями, вытекающими из векторной диаграммы установившегося режима [рис.2.1].