Понятие о динамической устойчивости.

То обстоятельство, что система сохраняет статическую устойчивость в уста­новившемся режиме работы, еще не позволяет утверждать, что она окажется устойчивой и при резких внезапных нарушениях режима ее работы, подоб­ных короткому замыканию (кз), отключению генераторов или линий и т. д. Эта сторона проблемы должна быть исследована самостоятельно и затра­гивает круг вопросов, относящихся к так называемой динамической устой­чивости электрических систем.

Таким образом, если при исследовании статической устойчивости приходится иметь дело с бесконечно малыми возмущениями рабочего режима работы системы (перерастающими в выпадение из синхронизма при неустойчивости системы), то предметом исследования динамической устойчивости являются значительные возмущения, причем существенное значение приобретают характер и размеры возмущения.

Для выяснения принципиальных положений динамической устойчивости мы рассмотрим явления, возникающие при внезапном отключении одной из двух параллельных цепей линии электропередачи (рис.2.4), связывающей удаленную станцию с шинами неизменного напряжения. Схема замещения электропередачи в нормальном режиме (до отключения цепи) представлена на рис.2.5. Индуктивное сопротивление системы, равное

х_с = х_Г + х_Т1 + + 0,5х_л + х_Т2,

определяет амплитуду характеристики мощности в этих усло­виях:

P_m = EU/x_c.

Опуская пока влияние переходных электромагнитных процессов в генераторах, можно установить, что при отключении одной из цепей линии электро­передачи индуктивное сопротивление системы получает новое значение (рис.2.11):

х_С = х_Г + х_Т1 + х_л + х_Т2

большее, чем в нормальном режиме, поскольку индуктивное сопротивление линии при отключении цепи возрастает 0,5х_Л до х_Л.

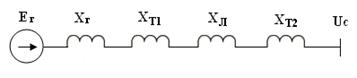
Рис. 2.11 Схема замещения электропередачи при отключении линии.

Амплитуда характеристики мощности при отключенной цепи соответственно уменьшается до EU/x_cl. Характеристики мощности в условиях нормального режима и при отключенной цепи показаны на рис.2.12. 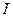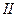Если режим работы, предшествовавший отключению цепи, определялся точкой а на характеристике мощности ( ) нормального режима при передаваемой мощности Р_о и угле ₀, то после отключения этому режиму должна соот­ветствовать новая характеристика мощности ( ), причем нетрудно устано­вить, какая именно точка этой характеристики будет определять режим в момент отключения цепи. Этой точкой является точка 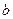при том же зна­чении угла 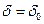, что и в нормальном режиме.

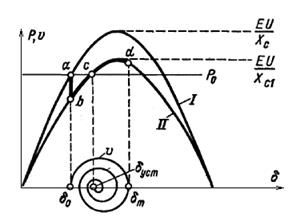
Рис. 2.12 Колебание угловой мощности и относительной угловой скорости генератора при отключении линии.

Угол сохраняет свое зна­чение 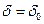в момент отключения, поскольку вектор эдс генератора 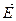может перемещаться относительно вектора напряжения приемной системы U только при изменениях частоты вращения ротора генератора. Частота же вращения ротора не может иметь скачкообразных изменений из-за существования механической инерции у ротора генератора.

Таким образом, в момент отключения цепи режим работы изменяется и характеризуется не точкой а, а точкой 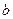на новой характеристике, что обусловливает внезапное уменьшение мощности генератора. Мощность тур­бины остается при этом неизменной и равной Р_о, так как регуляторы турбин реагируют на изменение частоты вращения агрегата, которая в мо­мент отключения цепи сохраняет свое нормальное значение, как это только что было отмечено.

В дальнейшем скорость машины будет изменяться, однако и в этой стадии процесса можно в первом приближении считать, что регуляторы не успевают сколько-нибудь заметно повлиять на мощность, развиваемую турбиной.

Неравенство мощностей, а, следовательно, и моментов на валу турбины и генератора вызывает появление избыточного момента, под влиянием которого агрегат турбина-генератор начинает ускоряться. Связанный с рото­ром генератора вектор эдс 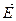начинает вращаться быстрее, чем вращаю­щийся с неизменной синхронной угловой скоростью 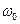вектор напряжения шин приемной системы U. 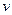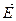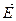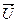Изменения скорости перемещения вектора эдс генератора относительно напряжения шин приемной системы U, представ­ляющей разность угловых скоростей вращения векторов и , показаны на рис. 2.12.

Возникновение относительной скорости вращения v приводит к увеличе­нию угла , и на характеристике мощности генератора при отклю­ченной цепи рабочая точка перемещается из точки 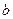по направлению к точке с. При этом мощность генератора начинает возрастать. Однако вплоть до точки с мощность турбины все еще превышает мощность генератора и избыточный момент, хотя и уменьшается, но сохраняет свой знак, благодаря чему относительная скорость вращения непрерывно возрас­тает. В точке с мощности турбины и генератора вновь уравновешивают друг друга и избыточный момент равен нулю. Однако процесс не оста­навливается в этой точке, так как относительная скорость вращения ротора достигает здесь наибольшего значения и ротор проходит точку с по инерции.

При дальнейшем росте угла мощность генератора уже превышает мощ­ность турбины и избыточный момент изменяет свой знак. Он начинает тормозить агрегат. Относительная скорость вращения v теперь уменьшается и в некоторой точке d становится равной нулю. Это означает, что в точке d вектор эдс 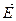и в некоторой точке d становится равной нулю. Это означает, что в точке d вектор эдс 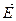вращается с той же угловой скоростью, что и вектор напряжения 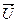, и, следовательно, угол между ними больше не возрастает. Угол в этой точке достигает своего максимального значения 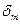. Однако и теперь процесс не останавливается, так как вследствие неравенства мощ­ностей турбины и генератора на валу агрегата существует избыточный момент тормозящего характера, под влиянием которого частота вращения продолжает уменьшаться и относительная скорость v становится отрица­тельной. Угол начинает уменьшаться, и рабочая точка, характеризующая процесс на характеристике мощности, перемещается в обратном направлении к точке с. Эту точку ротор вновь проходит по инерции, и около точки 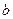угол достигает своего нового минимального значения, после чего вновь начинает возрастать. После ряда постепенно затухающих колебаний в точке с устанавливается новый установившийся режим с прежним значением пере­даваемой мощности Р_о и новым значением угла _уст. Картина колебаний угла во времени показана на рис.2.13. Постепенное уменьшение ампли­туды обусловливается потерями энергии при колебаниях частоты вращения генератора.

Такой характер перехода к новому режиму не влечет за собой каких-либо осложнений. Во всяком случае, в нарисованной картине нарушение устойчи­вости не имело места. Можно отметить лишь, что в переходном электро­механическом процессе угол достигал значений ( 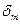), превышающих значе­ние _уст нового установившегося режима.

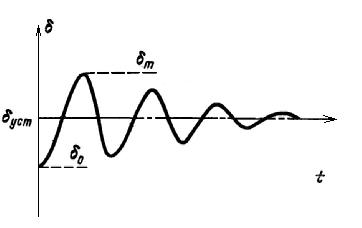
Рис.2.13 Колебания угла при отключении одной линии.

Возможен и другой исход процесса (рис.2.14). Торможение ротора, начиная с точки с, уменьшает относительную скорость вращения v. Однако угол в этой фазе процесса все еще возрастает, и если он успеет достигнуть критической величины _кр в точке с на пересечении падающей ветви сину­соиды мощности генератора с горизонталью мощности турбины Р_о прежде, чем относительная скорость v упадет до нуля, в дальнейшем избыточный момент на валу машины становится вновь ускоряющим, скорость v начнет быстро возрастать и генератор выпадает из синхронизма (рис.2.15).

Таким образом, если в процессе качаний будет пройдена точка с', то возврат к установившемуся режиму уже невозможен.

Итак, можно констатировать, что, несмотря на теоретическую возмож­ность существования нового установившегося (и статически устойчивого) режима в точке с, процесс качания машины при переходе к этому режиму может привести к выпадению машины из синхронизма. Такой характер нарушения устойчивости может быть назван динамическим.

Основной причиной нарушений динамической устойчивости электрических систем являются обычно короткие замыкания, резко уменьшающие ампли­туду характеристики мощности.

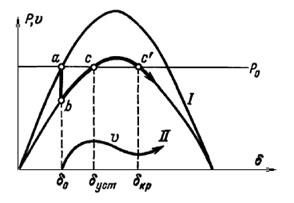
Рис.2.14 Нарушение динамической устойчивости при отключении одной линии.

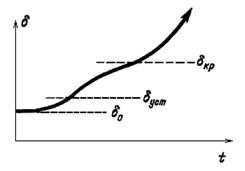
Рис.2.15 Нарастание угла при нарушении устойчивости.