Эмиссионное смещение как переход процессов.

Рассмотрим функцию F_BK1. На рисунке 5.39. видно, что эмиссионное смещение – это пучок прямых с совсем другими параметрами. На рисунке 5.39. мы получили график для режима больших токов.

Но существует также математическая модель для вольт-амперной характеристики в области эмиссионного смещения – области режима малых токов. Область малых токов моделируется эмиссионным уравнением с другими параметрами.

Приведём математическую модель для режима малых токов на рисунке 5.41.

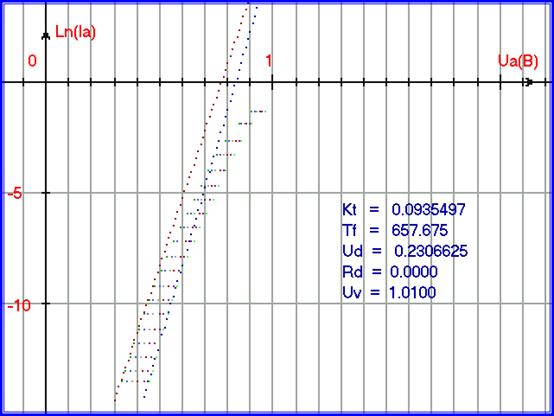
Рис. 5.41. Вольт-амперные характеристики прямого тока математической модели для функции F_BK1:ВАХ PN-перехода база-коллектор при разомкнутых выводах база - эмиттер, для температур 10, 20, 30, 40, 50, 60 градусов по Цельсию для транзистора КТ312В. Графики модели для температур 10 и 60 градусов по Цельсию построены поверх графиков точек экспериментальных данных. Математическая модель построена для начального участка – для режима малых токов.

Для рисунков 5.39. и 5.41. можно сделать некоторые наблюдения. В результате изменения аргумента Ua, происходит переход процессов. В результате перехода процессов, при росте Ia мы наблюдаем, что температура T_F от значения 657 Кельвин переходит к значению 938 Кельвин. И очень важно обратить внимание на изменения смещения характеристик: для режима малых токов Uv = 1,01 Вольт, для режима больших токов Uv = 1,198 Вольт.

Малые токи смещены относительно больших токов - на 0,188 Вольта.

Uv2 – Uv1 = 0,188 Вольт. (5.6.12.,04)

Рассмотрим вопрос создания модели на основе процессорного перехода для функции F_BK1. Эта модель должна начинаться (режим малых токов) как эмиссионное уравнение с параметрами на рисунке 5.39., а заканчиваться (режим больших токов) как эмиссионное уравнение с параметрами на рисунке 5.41.

Такую математическую модель можно создать при помощи процессового перехода. Процессами будут два эмиссионных уравнения с разными параметрами. В качестве внешней функции используем степенную функцию с показателем степени 20. Процессовый переход будет выражаться следующей формулой:

Ia = A = exp( K_T1 ∙ ( T∙ U_D1 - ( T- T_F1 ) ∙ (Ua – Uv1 – Ia ∙ R_D1 ) ) )

Ia = B = exp( K_T2 ∙ ( T∙ U_D2 - ( T- T_F2 ) ∙ (Ua – Uv2 – Ia ∙ R_D2 ) ) )

_N ______________

Ia _рез = A∙B / √ ( A^N + B^N

N = 20

Ia _рез - результирующий прямой ток перехода база-коллектор для схемы измерения функции F_BK1. Приведём наборы параметров для двух эмиссионных уравнений функции F_BK1.

N = 20,00000000

Для режима малых токов:

Kt1 = 0,09354973

Tf1 = 657,67532468

Uv1 = 1,01289594

Ud1 = 0,23066250

Rd1 = 0

Для режима больших токов:

Kt2 = 0,03613718

Tf2 = 938,55555556

Uv2 = 1,19732492

Ud2 = 0,55400841

Rd2 = 0,25512936

На рисунке 5.42. построим математическую модель Ia _рез .

Рис. 5.42. Вольт-амперные характеристики прямого тока математической модели для функции F_BK1:ВАХ PN-перехода база-коллектор при разомкнутых выводах база - эмиттер, для температур 10, 20, 30, 40, 50, 60 градусов по Цельсию для транзистора КТ312В. Графики модели для температур 10 и 60 градусов по Цельсию построены поверх графиков точек экспериментальных данных. Математическая модель построена для начального участка – для режима малых токов и конечного участка – режима больших токов.

На рисунке 5.42. мы можем видеть, что график математической модели и графики экспериментальных данных (для температур 10 и 60 градусов по Цельсию) совпадают.

С точки зрения программирования – построение графика реализуется обращением к процедуре MidI3 из функции, которая вычисляет процессовый переход. Такой вид вычислений не представляет труда для современной вычислительной техники. Приведём пример реализации полной математической модели для F_BK1 на функциях и подпрограммах Delphi.

procedure MidI3(x,z,Tf,Ud,Kt,Uv,Rd:real;var y:real;var c0:integer);

var

Ymax, Ymin, X0, E: real;

Ub,Uf:real;

A,B,C,D:real;

begin

c0:=0;

E:=0.000001;

Ymax:=exp(((Tf-z)*x + z*Ud)*Kt);

Ymin:=0;

repeat

begin

y:=(Ymax+Ymin)/2;

Ub:= Uv+ y*Rd;

if y<=0 then

begin

break;

c0:=1;

end;

A:=Ln(y);

B:=A/(-Kt);

C:=B+z*Ud;

D:=z-Tf;

if D=0 then

begin

break;

c0:=2;

end;

X0:=(C/D)+Ub;

if X0 > x then Ymax:=y else Ymin:=y;

end until (X0+E > x) and (X0-E < x);

end;

//////////////////////////////////////////////////////////////////////////

function I_Fbk1S(Ua,T:real; var c00:integer):real;

var

Tf1,Ud1,Kt1,Rd1,Uv1:real;

Tf2,Ud2,Kt2,Rd2,Uv2:real;

A9,B9,C9,N9,Ia:real;

begin

c00:=0; // сброс кода ошибки

Kt1:= 0.09354973;

Tf1:= 657.67532468;

Uv1:= 1.01289594;

Rd1:=0;

Ud1:= 0.23066250;

Kt2:= 0.03613718;

Tf2:= 938.55555556;

Uv2:= 1.19732492;

Rd2:= 0.55400841;

Ud2:=0.554008;

N9:=20;

MidI3(Ua,T,Tf1,Ud1,Kt1,Uv1,Rd1,A9,c00);

MidI3(Ua,T,Tf2,Ud2,Kt2,Uv2,Rd2,B9,c00);

Ia:=A9*B9/(Power(( Power(A9,N9)+Power(B9,N9) ) ,(1/N9)));

I_Fbk1S:=Ia;

end;

Прямая функция I_Fbk1S успешно вычисляется, но теперь возникает задача: как из функции F_BK1 вычислить её обратную функцию. Решение такой задачи опять же позволяет реализовать вычислительная техника. Используя легкость вычисления функции I_Fbk1S можно создать на Delphi функцию, вычисляющую Ua, U_Fbk1S :

//////////////////////////////////////////////////////////////////////////

function U_Fbk1S(y,T:real; var c0:integer):real;

var

Xmax, Xmin, Y0, E, x: real;

L0:integer;

begin

// x это Ua

// y это Ia

// T - температура

c0:=0;

E:=0.0000001; // точность Ia - для расчёта Uà

Xmax:=2.5; // Ua более чем 2.5 В в практике встречается редко

Xmin:=0;

repeat

begin

x:=(Xmax+Xmin)/2;

Y0:=I_Fbk1S(x,T,L0);

// аварийный выход при ошибке в I_Fbk1S(x,T,L0);

if L0<>0 then

begin

c0:=L0; // передача кода ошибки

exit;

end;

if Y0 > y then Xmax:=x else Xmin:=x;

end until (Y0+E > y) and (Y0-E < y);

U_Fbk1S:=x;

end;

Вопросы создания подпрограмм и функций очень важны для процесса математического моделирования. Другой способ моделирования реализовать, вероятно, очень сложно.

Наличие процессового перехода говорит о существовании в функции F_BK1 обратных связей. См. главы 5.2.4., 5.3.1..

Можно убедиться, что функции F_BE1 и F_BK0, обладающие эмиссионным смещением, также моделируются процессовым переходом.

На рисунке 5.43. приведём график математической модели для режима малых токов функции F_BE1.

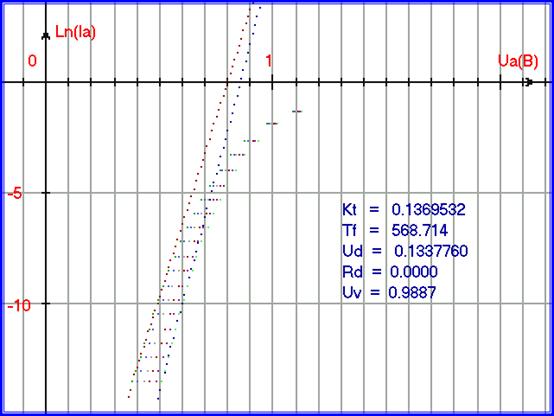
Рис. 5.43. Вольт-амперные характеристики прямого тока математической модели для функции F_BE1:ВАХ PN-перехода база-эмиттер при разомкнутых выводах база - коллектор, для температур 10, 20, 30, 40, 50, 60 градусов по Цельсию для транзистора КТ312В. Графики модели для температур 10 и 60 градусов по Цельсию построены поверх графиков точек экспериментальных данных. Математическая модель построена для начального участка – для режима малых токов.

Приведём наборы параметров для 2-х эмиссионных уравнений функции F_BE1.

N = 20,00000000

Для режима малых токов:

Kt1 = 0,13695315

Tf1 = 568,71428571

Uv1 = 0,98779546

Ud1 = 0,13377596

Rd1 = 0

Для режима больших токов:

Kt2 = 0,06289079

Tf2 = 666,33333333

Uv2 = 1,12206544

Ud2 = 0,18393456

Rd2 = 0,79836467

Сравнивая функции F_BK1 и F_BE1 можно заметить, что коллекторный переход достигает более высокой температуры T_F.

У эмиттерного PN-перехода - максимум T_F = 666,3 Кельвин.

У коллекторного PN- перехода - максимум T_F = 938,5 Кельвин.

На рисунке 5.44. по методу процессового перехода с внешней степенной функцией, построим математическую модель функции F_BE1.

Рис. 5.44. Вольт-амперные характеристики прямого тока математической модели для функции F_BE1:ВАХ PN-перехода база-эмиттер при разомкнутых выводах база - коллектор, для температур 10, 20, 30, 40, 50, 60 градусов по Цельсию для транзистора КТ312В. Графики модели для температур 10 и 60 градусов по Цельсию построены поверх графиков точек экспериментальных данных. Математическая модель построена для начального участка – для режима малых токов и конечного участка – режима больших токов.

На рисунке 5.44. можно заметить, что график математической модели и графики экспериментальных данных совпадают.

Для функции F_BK0 на рисунке 5.45. построим математическую модель для малых токов.

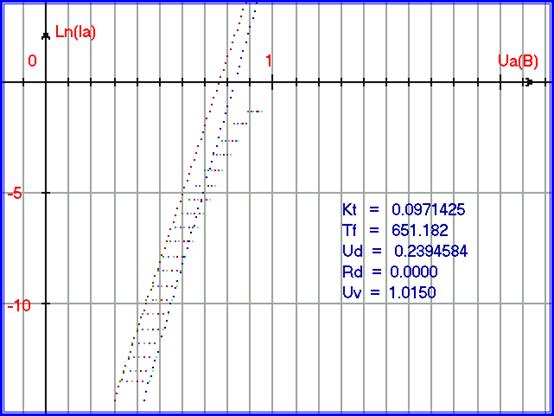
Рис. 5.45. Вольт-амперные характеристики прямого тока математической модели для функции F_BK0 для малых токов:ВАХ PN-перехода база-коллектор при разомкнутых выводах база - эмиттер, для температур 10, 20, 30, 40, 50, 60 градусов по Цельсию для транзистора КТ312В. Графики модели для температур 10 и 60 градусов по Цельсию построены поверх графиков точек экспериментальных данных. Математическая модель построена для начального участка – для режима малых токов.

Приведём наборы параметров для 2-х эмиссионных уравнений функции F_BK0.

N = 20,00000000

Для режима малых токов:

Kt1 = 0,09714249

Tf1 = 651,18181818

Uv1 = 1,01399614

Ud1 = 0,23945840

Rd1 = 0

Для режима больших токов:

Kt2 = 0,04520663

Tf2 = 843,00000000

Uv2 = 1,16652465

Ud2 = 0,47047535

Rd2 = 0,30014988

На рисунке 5.46 приведём математическую модель для функции F_BK0 выполненную на основе процессового перехода.

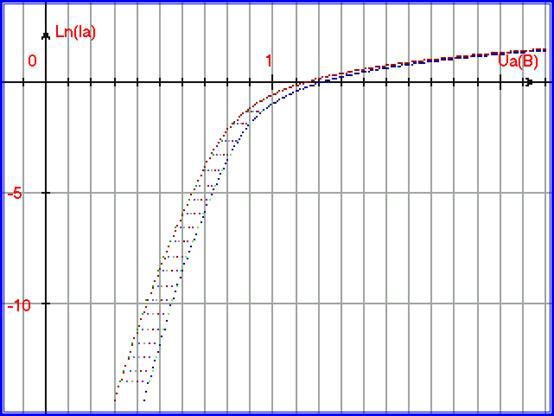
Рис. 5.46. Вольт-амперные характеристики прямого тока математической модели для функции F_BK0:ВАХ PN-перехода база-коллектор при замкнутых выводах база - эмиттер, для температур 10, 20, 30, 40, 50, 60 градусов по Цельсию для транзистора КТ312В. Графики модели для температур 10 и 60 градусов по Цельсию построены поверх графиков точек экспериментальных данных. Математическая модель построена для начального участка – для режима малых токов и конечного участка – режима больших токов.

На рисунке 5.46. можно заметить, что график математической модели и графики экспериментальных данных совпадают.

Функция F_BE0 не имеет участка эмиссионного смещения. Это значит, что при замкнутом коллекторном PN-переходе, эмиттерный

PN-переход можно моделировать одним эмиссионным уравнением.

Остальные функции – F_BE1, F_BK0, F_BK1 – были нами исследованы, математические модели были получены. Все они показывают, что эмиттерный переход и коллекторный переход находятся в состоянии обратной связи. Эта связь отрицательная, так, как вызывает смещение вольт-амперных характеристик вправо (уменьшение тока) в режимах малых токов. Малые токи наиболее чувствительны к тепловому инжекционному току, идущего от смежного перехода в результате зеркального отражения.

Наибольшая польза от проделанной работы – это полученные математические модели. Они будут нужны при исследовании двух основных схем работы биполярного транзистора – схемы с общим эмиттером и схемы с общей базой.

Моделирование процессовым переходом по принципу минимизации подходит лишь для тех вольт-амперных характеристик, где существует эмиссионное смещение.