Модель межотраслевого баланса и ее значение

Модель Вальраса описывает не только оптимальное состояние экономической системы, она дает еще и формальное выражение всеобщей зависимости цен, складывающихся в результате сделок на одних рынках, от цен, возникающих на других рынках. Межотраслевой баланс В. Леонтьева впоследствии позволил дать этой всеобщей связи количественное выражение; в свою очередь, модель межотраслевого баланса, чаще всего используемая в анализе функционирования реальных экономических систем, основывается на допущении о линейных производственных функциях. Таким образом, в модели межотраслевого баланса напрямую реализуется подход к экономике как системе взаимозависимых отраслевых рынков, предложенный в свое время Л. Вальрасом.

Как определить влияние изменений цен в одной отрасли на спрос и предложение в других отраслях? И как это повлияет на экономический рост? И – в конечном счёте – развитие какие отраслей приведёт к максимальному росту валового внутреннего продукта при отраслевых сдвигах?

Начнем с анализа материальных затрат – валового продукта, включающего в себя весь межотраслевой оборот. Представим материальные затраты в виде совокупности чистых отраслей:

Выпуск затраты	Сельское хозяйство	Добывающая промышленность
Сельское хозяйство	X11	X12		X1n	(Xi)
Добывающая промышленность	X21	X22		X2n
			[Xij]
	Xn1	Xn2

(X_j)

Табл.4.1. Первый квадрант межотраслевого баланса

Каждый x_i в этой матрице представляет собой объем поставки продукции i-той отрасли во все остальные отрасли хозяйства. Каждый x_j – затраты на производство продукции в отрасли j. Таким образом, каждый из x_ij можно представить в двух срезах - как распределение выпуска (поставки) и затрат.

Очевидно, 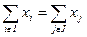. И в то же время совпадение x_i=x_j при i=j возможно только в редчайших случаях. Выпуск в какой-то отрасли может быть существенно выше, чем затраты, в этом случае в этой отрасли возникает излишек денежных средств (отраслевые сбережения). Однако и затраты в отрасли могут быть выше, чем выпуск за счёт инвестиций в развитие этой отрасли (скажем, строятся новые заводы, которые потом будут производить продукцию, в настоящее же время затраты на приобретение нового оборудования, монтаж, строительство учитываются как отраслевые затраты).

Введем допущение об однородности производственных функций, описывающих формирование затрат и выпуска в межотраслевом балансе (МОБ):

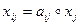, отсюда ,

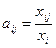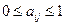
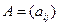– матрица прямых затрат; 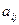– коэффициент прямых затрат продукции i на производство продукции j или, что то же самое, удельный вес поставок отрасли i в отрасль j. Отсюда можно записать:

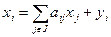, где:

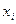– валовый продукт, включающий в себя межотраслевой оборот (т.е. не только конечное, но и производственное потребление);

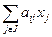– материальные затраты, промежуточный продукт,

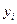– конечный (чистый) продукт (собственно ВВП),

или ,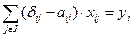

где ,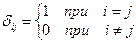

В векторно-матричной форме:

;

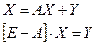где .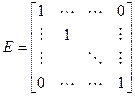

Таким образом, получили уравнение, описывающее взаимозависимость между валовым и конечным продуктом. Это – основное уравнение модели межотраслевого баланса. Сам же межотраслевой баланс выглядит следующим образом:

Распределение продукции     Затраты на производство

Текущее производственное потребление в отраслях

Конечная продукция (по элементам)

Валовой продукт

1 2 3 4 ……………n

Итого

Материальные затраты в отраслях

. . . . . . . n

xij   квадрант I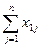

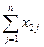
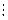
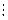
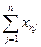
y1 y2 y3 . . . . квадрант II . . . yn

x1 x2 x3 . . . . . . . . xn

Баланс

Итого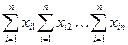

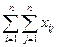
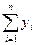
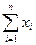
Условно-чистая продукция (по элементам: амортизация, заработная плата, прибыль)

z1 z2 z3 ……………zn   квадрант III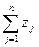

квадрант IV

Валовой продукт

x1 x2 x3 ……………xn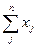

Баланс

Табл. 4.2. Межотраслевой баланс

I-й квадрант – межотраслевые взаимосвязи по использованию продукции на текущее производственное потребление;

II-й квадрант – материально-вещественный состав валового внутреннего продукта (ВВП по расходам: потребление, валовые инвестиции, государственные закупки в разрезе отраслей);

III-й квадрант – стоимостной состав валового продукта «по доходам» (заработная плата, прибыль, процент, дивиденды, рента, налоговые платежи и т.д. в разрезе отраслей);

IV-й квадрант – перераспределение конечной продукции.

Выделяют два баланса "внутри" МОБ:

- материальный: I и II квадранты,

- баланс затрат: III и IV квадранты.

Уравнение материального баланса:

;

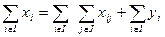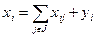
Уравнение баланса затрат:

;

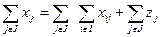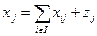
Перераспределяя конечную продукцию с помощью государственного регулирования — будь-то налоги, государственные инвестиции или другие экономические рычаги, государство влияет на структуру I квадранта. Впоследствии же любое изменение потоков поставок из отрасли в отрасль изменит в свою очередь значение как Y (ВВП, взятого в разрезе расходов), так и Z (ВВП, взятого в разрезе доходов). Допуская постоянство матрицы прямых затрат, можно рассчитать изменения соотношения конечного и валового национального продукта; "облегчить" или "утяжелить" структуру хозяйства (чем меньше это соотношение, тем более "тяжелая" структура). Нахождение оптимальной структуры совпадает также с равновесием по Вальрасу и состоянием межхозяйственного оптимума.