Определение характеристик явления рассеяния
При изготовлении партии деталей по одному и тому же технологическому процессу, одним и тем же рабочим, на одном и том же рабочем месте, в одних и тех же условиях наблюдаются отклонения значений параметров точности деталей от идеального прототипа и друг от друга. Это явление получило название рассеяние.
На всех этапах технологического процесса изготовления детали действует большое количество непрерывно или дискретно изменяющихся случайных и систематических факторов.
Систематические факторы бывают:
– постоянно действующие (например, погрешность формы обрабатываемой поверхности, обусловленная непараллельностыо оси шпинделя направляющим токарного станка; погрешность измерения и др);
– изменяющиеся по определенному закону у = f(x)(например, размерный износ инструмента, тепловые деформации станка и др.).
Случайные факторы характеризуются большим их количеством, отсутствием связи между собой и нестабильностью (например, упругие отжатия звеньев системы СПИД).
На практике явление рассеяния любой характеристики качества изучается с помощью точечной диаграммы, которая позволяет определить все характеристики.
Для построения точечной диаграммы по оси абцисс откладываются порядковые номера измерений деталей, а по оси ординат в виде точек – полученные значения соответствующего номера измерений деталей (рис. 1.1). Через точки, соответствующие максимальному и минимальному значениям измерения, проводятся две линии, параллельные между собой и оси абцисс. Расстояние между этими линиями является первой характеристикой рассеяния значений и носит название поля рассеяния ω = Анб– Aнм. Эта характеристика обязательно дополняется координатой середины поля рассеяния – ∆ω, которая представляет собой расстояние между серединой поля рассеяния и номинальным значением. Она определяет положение поля рассеяния относительно номинала.
Второй характеристикой явления рассеяния служит практическая кривая рассеяния и определяющие ее параметры. Для построения практической кривой рассеяния необходимо поле рассеяния ω на точечной диаграмме разделить на 7…11 интервалов линиями, параллельными оси абцисс. В каждом интервале подсчитать количество попавших в него результатов измерений (абсолютная частость т) и изобразить это количество в виде прямоугольников шириной, равной величине интервала, и высотой, равной абсолютной частости т.
Получившаяся диаграмма называется гистограммой рассеяния. Изобразив абсолютную частоту т в виде прямых линий, расположенных посредине каждого интервала (нагруженных ординат), и соединив их верхние точки отрезками прямых линий, получают ломаную линию, называемую практической кривой рассеяния значений измерения (рис. 2.1).
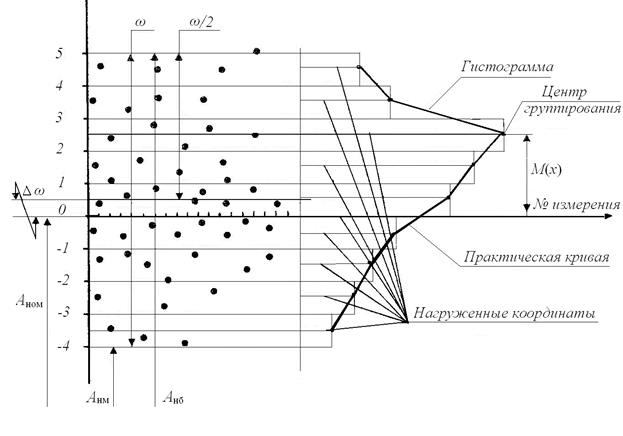 |
Pиc. 1.1. Точечная диаграмма и практическая
кривая рассеяния значений измерения
Параметрами, характеризующими практическую кривую рассеяния, являются:
1. Уравнение кривой рассеяния у = φ(х). Для большинства задач оценки точности в технологии машиностроения распределение текущих значений хiподчиняется нормальному закону (закону Гаусса), для которого
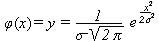 . (2.1)
. (2.1)
Кроме закона Гаусса текущие значения хi могут распределяться по закону равной вероятности, закону Симпсона, закону Шарлье и др.
2. Центр группирования случайной величины – это среднее значение, около которого располагается наибольшее количество значений. Иными словами, центр группирования – это значение случайной величины, принадлежащее большинству деталей в партии. Положение центра группирования определяется координатой центра группирования (математическим ожиданием) M(x).
3. Среднее квадратичное отклонение σ, показывающее плотность группирования текущих значений относительно центра группирования М(х). Графически σ изображается в виде двух абцисс, равноотстоящих от значения  M(x) на величину σ, Эта характеристика служит мерой рассеяния.
M(x) на величину σ, Эта характеристика служит мерой рассеяния.
4. Коэффициент относительной асимметрии а, показывающий смещение центра группирования М(х)относительно середины поля рассеяния. Для дискретных величин текущего значения хiхарактеристики M(x), σ и а определяются по равенствам:
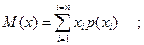 (2.2)
(2.2)
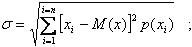
 (2.3)
(2.3)
 (2.4)
(2.4)
где р(хi) = т/п –количество значений измерений, попавших в соответству-ющий интервал, выраженное в процентах или долях всего количества измеренных величин (относительная частость).
Вычисленные характеристики рассеяния значений измерения представляются в графическом виде, учитывая, что уmах ≈ 0,4/σ, уσ ≈ 0.24/σ (рис. 2.2).
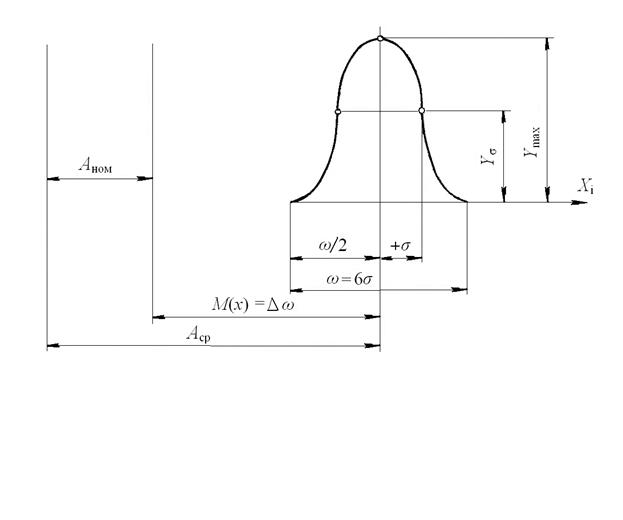
Рис. 2.2. Характеристики явления рассеяния: M(x); σ ; а
Лабораторная работа выполняется двумя бригадами. Явление рассеяния в данной работе изучается на примере двух партий деталей по 50 штук номиналами А1, А2.
Произвести установку (50 раз) заготовки в трёхкулачковый патрон и измерить осевое смещение.
При установке деталь необходимо плотно прижимать торцовой поверхностью к оснастке, а при повторных установках деталь необходимо поворачивать вокруг ее оси на некоторый угол.
Результаты измерений зафиксировать после каждой установки детали.
По результатам измерений построить точечную диаграмму, гистограмму и кривую рассеяния аналогично этапу 2.
Определить параметры, характеризующие кривую рассеяния, аналогично этапу 3.
Сравнить результаты экспериментов и сделать выводы.
Построить схему этих характеристик явления рассеяния (рис.2.2).
Дата добавления: 2020-10-14; просмотров: 810;











