Анализ сложных электрических цепей постоянного тока.
Метод законов Кирхгофа
Сложной электрической цепью принято называть разветвленную цепь, содержащую несколько источников, расположенных в разных ветвях. Пример сложной цепи постоянного тока приведен на рис. 22.
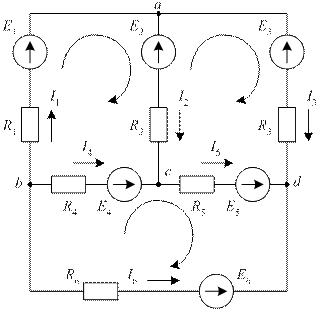
Рис. 22. Пример сложной цепи постоянного тока
Истинные направления токов в ветвях сложной электрической цепи, как правило, неизвестны. Поэтому анализ сложной цепи начинается с выбора так называемых положительных направлений токов в ветвях схемы. На схеме положительные направления токов в ветвях обозначают стрелками с символами тока I. Пример выбора условных положительных направлений токов в ветвях схемы показан на рис. 22.
Если в результате анализа цепи получается, что ток в ветви положителен, то истинное направление тока будет совпадать с выбранным положительным направлением тока. Если в результате расчета окажется, что ток в ветви отрицателен, то истинное направление тока противоположно выбранному положительному направлению тока. Т.е. в ходе анализа электрической цепи токи в ветвях рассматриваются как алгебраические величины.
Наиболее общий подход к анализу сложных электрических цепей основан на использовании законов Кирхгофа. С помощью законов Кирхгофа составляется система линейных алгебраических уравнений относительно неизвестных токов. Число неизвестных токов равно числу ветвей схемы. Обозначим это число через m. Следовательно, с помощью законов Кирхгофа необходимо составить систему из m уравнений с m неизвестными токами.
При составлении уравнений по законам Кирхгофа необходимо придерживаться следующего правила. Если в схеме n узлов, то с помощью первого закона Кирхгофа составляется (n – 1) независимое уравнение. (Уравнение для последнего узла будет зависимым). Оставшиеся [m–(n –1)] уравнения составляются с помощью второго закона Кирхгофа для так называемых независимых контуров.
Независимый контур – это такой контур, при обходе которого появляется хотя бы одна новая ветвь по сравнению с ранее рассмотренными контурами.
В разветвленной цепи число независимых контуров всегда меньше общего количества контуров. Поэтому при выборе независимых контуров имеется определенная свобода выбора. Однако число независимых контуров в схеме всегда регламентировано. Схема рис. 22, например, содержит
[m – (n – 1)] = [6 – (4 – 1)] = 3
независимых контура.
В результате составления (n – 1) уравнения по первому закону Кирхгофа и [m – (n – 1)] уравнения по второму закону Кирхгофа образуется система из m уравнений относительно неизвестных токов ветвей. Решение этой системы позволяет определить токи ветвей.
Схема рис. 22 состоит из шести ветвей. Выбранные положительные направления токов в ветвях указаны на схеме стрелками с символами тока I1, I2, I3, I4, I5, I6. Для расчета токов в ветвях этой схемы с помощью законов Кирхгофа необходимо составить систему из шести уравнений.
Схема содержит четыре узла (n = 4). По первому закону Кирхгофа необходимо составить три уравнения. Условимся при составлении уравнений по первому закону Кирхгофа токи, выходящие из рассматриваемого узла, брать со знаком «плюс», а входящие в узел, – со знаком «минус».
В узел а входит ток I1, а выходят токи I2 и I3. Тогда для узла a уравнение первого закона Кирхгофа будет иметь вид
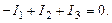
Из узла b выходят токи I1, I4, I6. Уравнение первого закона Кирхгофа для узла b имеет вид
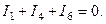
В узел c входят токи I2 и I4, а выходит ток I5. Поэтому для узла c можно записать
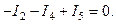
Уравнения первого закона Кирхгофа, составленные для узлов а, b, c, включают в себя токи всех шести ветвей рассматриваемой схемы. Суммируя уравнения, составленные по первому закону Кирхгофа для узлов а, b, c, получаем следующее уравнение:
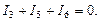
Это уравнение отличается от уравнения первого закона Кирхгофа для узла d только знаками, а именно:
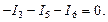
То есть, уравнение первого закона Кирхгофа для узла d зависимое.
По второму закону Кирхгофа для рассматриваемой схемы необходимо составить три уравнения для трех независимых контуров. В качестве независимых контуров можно рассматривать, например, левый контур, составленный из первой, второй и четвертой ветвей, правый контур, составленный из второй, третьей и пятой ветвей, и нижний контур, составленный из четвертой, пятой и шестой ветвей.
При составлении уравнения второго закона Кирхгофа для каждого независимого контура необходимо придерживаться следующего правила. Если выбранное положительное направление тока в ветви совпадает с направлением обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если выбранное положительное направление тока в ветви противоположно направлению обхода контура, то падение напряжения на соответствующем элементе R в левой части уравнения второго закона Кирхгофа берется со знаком «минус». Если направление действия источника ЭДС, указанное на схеме стрелкой, совпадает с направлением обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «плюс». Если направление действия источника ЭДС, указанное на схеме стрелкой, противоположно направлению обхода контура, то соответствующая ЭДС Е в правой части уравнения второго закона Кирхгофа берется со знаком «минус».
Направления обхода независимых контуров на схеме рис. 22 выберем по часовой стрелке. Эти направления обхода указаны на схеме стрелками, замыкающимися вдоль каждого из независимых контуров.
Рассмотрим поочередно каждый из независимых контуров. В левом контуре токи I1 и I2 совпадают с направлением обхода контура. Падения напряжений R1I1, R2I2 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «плюс».Ток I4 имеет направление, противоположное направлению обхода левого контура. Падение напряжения R4I4 в левой части уравнения второго закона Кирхгофа для левого контура необходимо взять со знаком «минус». Направление действия источника ЭДС Е1 совпадает с направлением обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е1 необходимо взять со знаком «плюс». Направления действия источников ЭДС Е2 и Е4 противоположны направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е2 и Е4 необходимо взять со знаком «минус». Таким образом, для левого независимого контура справедливо следующее уравнение второго закона Кирхгофа:
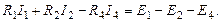
Аналогично для правого и нижнего независимых контуров схемы рис. 22 получаем следующие уравнения второго закона Кирхгофа:
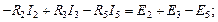
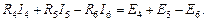
При объединении уравнений, составленных по первому и второму законам Кирхгофа для схемы рис. 22, получается следующая система линейных алгебраических уравнений:
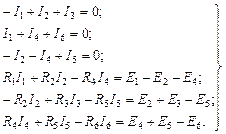
Решение этой системы позволяет найти токи I1, I2, I3, I4, I5, I6. По известным токам можно найти падения напряжений на элементах схемы, мощности и так далее.
Изложенный метод анализа сложных электрических цепей носит название метода законов Кирхгофа. Метод законов Кирхгофа – это наиболее общий подход к анализу электрических цепей.
Для анализа сложных электрических цепей могут использоваться и другие методы, например, метод контурных токов, метод узловых потенциалов, метод наложения, метод эквивалентного генератора. Эти методы строятся на основе законов Кирхгофа, закона Ома, принципа наложения. Поэтому они справедливы для линейных цепей. Исключение составляет метод эквивалентного генератора, который предполагает, что ветвь с искомым током может быть и нелинейной. Многообразие методов анализа сложных электрических цепей позволяет в каждом конкретном случае выбрать тот метод, который дает наиболее простой алгоритм расчета.
В частности, метод контурных токов и метод узловых потенциалов подобно методу законов Кирхгофа сводятся к решению систем линейных алгебраических уравнений. Однако количество искомых величин, а, следовательно, и порядок систем линейных алгебраических уравнений в этих методах меньше, чем в методе законов Кирхгофа.
Для решения систем линейных алгебраических уравнений используются известные математические методы. При малом количестве уравнений в системе можно использовать метод определителей (правило Крамера). При достаточно большом количестве уравнений в системе целесообразно использовать метод последовательного исключения неизвестных Гаусса с выбором главного элемента или итерационные методы решения систем линейных алгебраических уравнений, например, метод Зейделя.
Проверку правильности полученного решения можно выполнить путем подстановки найденных значений токов ветвей в систему уравнений, составленную по законам Кирхгофа, или путем составления баланса мощностей (смотри ниже).
Рассмотрим поочередно основные методы анализа электрических цепей. Но предварительно рассмотрим общий вопрос, касающийся геометрической структуры электрических цепей.
Дата добавления: 2016-06-29; просмотров: 6468;











