Постановка задачі нелінійного програмування та її характерні особливості

До цього часу ми розглядали задачі лінійного програмування, тобто всі невідомі і в цільову функцію, і в обмеження задачі входили лінійно. Проте взаємозв’язки між економічними показниками досить часто носять нелінійний характер і побудована лінійна модель в такому випадку буде неадекватна реальній дійсності. Тому доцільно досліджувати певні економічні пронеси з допомогою нелінійних моделей, математичним інструментом яких є нелінійне програмування.

В загальному випадку задача нелінійного програмування має вигляд:

Z = f(x₁,x₂,...,x_n) max(min), (7.1)

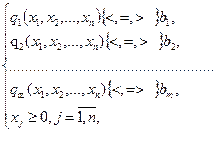(7.2)

де f(x₁,x₂,...,x_n) та 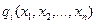- нелінійні функції.

Часто задачу нелінійного програмування намагаються привести до лінійного виду. Для лінійних задач завжди можна знайти оптимальний розв’язок універсальним (симплексним) методом. При цьому немає проблеми з доведенням існування такого розв’язку, адже в результаті розв’язання задачі симплексним методом завжди отримуємо один із варіантів відповіді:

1) знайдено оптимальний розв’язок;

2) задача суперечлива, тобто її розв’язку не існує;

3) цільова функція необмежена, отже, розв’язку також немає.

Для задач нелінійного програмування не існує універсального методу розв’язування, тому кожного разу треба доводити існування розв’язку задачі, а також його єдиність. При розв’язуванні нелінійних задач використовують наближені методи, більшість яких дають змогу знаходити локальні оптимуми, а вже знайшовши всі локальні оптимуми, методом порівняння значень цільової функції у кожній з точок локального оптимуму можна знайти глобальний.