Прикладні моделі задач цілочислового лінійного програмування (модель формування оптимальної інвестиційної програми при заданому бюджеті)

У окресленій моделі цільовою функцією виступає вартість капіталу інвестиційної програми, причому в ній при заданих обмеженнях (конкретної виробничої програми для окремих інвестиційних об’єктів і за наявності повного обсягу фінансових ресурсів) необхідно сформувати та визначити інвестиційну програму.

Для побудови моделі зробимо такі припущення:

1) представлені на вибір інвестиційні об’єкти рівнозначні;

2) фінансові ресурси неможливо залучити в необмеженій кількості за вказаною відсотковою ставкою;

3) інвестиційна програма визначається тільки на початок планового періоду, а початкові витрати при цьому не перевищують зазначений бюджет;

4) інвестиційні об’єкти реалізуються як єдине ціле.

Для побудови моделі введемо такі позначення: і – індекс інвестиційного об’єкта, 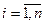; С_і - вартість капіталу і-гоінвестиційного об’єкта; А_і0 - затрати на придбання і-гоінвестиційного об’єкта; Q - загальний обсяг бюджетних коштів; х_і - бінарна змінна (х_і = 0 або 1), значення якої визначає, буде для і-го інвестиційного об’єкта виділене фінансування чи ні.

Враховуючи введені позначення, економіко-математична модель формування оптимальної інвестиційної програми при окресленому бюджеті матиме вигляд.

Знайти такий розв’язок 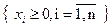, який забезпечить сумарну максимальну вартість інвестиційної програми:

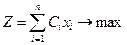(6.6)

при умовах:

1) з використання наявного обсягу бюджетних коштів

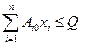(6.7)

2) з реалізації інвестиційних об’єктів як єдиного цілого (неподільності інвестиційних об’єктів)

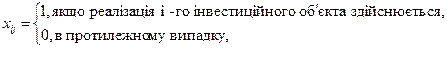
Таким чином, ми отримали задачу лінійного програмування з бульовими змінними. Розв’язок цієї задачі можна знайти з допомогою процедури цілочислового програмування.