Постановка задачі динамічного програмування

Динамічне програмування - це математичний апарат, який дозволяє швидко знаходити оптимальне рішення у випадку, коли ситуація, що вивчається, має велику кількість варіантів поведінки, які дають різні результати і серед них треба вибрати найкращий. Динамічне програмування використовують при розв’язуванні певного типу задач шляхом їх розкладу на менші та простіші підзадачі. Розв’язок такого виду задачі можна знайти шляхом перебору всіх можливих варіантів і вибору серед них найкращого, але в більшості випадків такий перебір є досить трудомістким. Тому процес прийняття оптимального рішення розбивається на етапи (кроки) і досліджується з допомогою методу динамічного програмування.

Динамічне програмування використовується для розв’язання таких задач: розподіл дефіцитних капітальних вкладень між новими напрямками їх використання; розробка сценаріїв управління попитом чи запасами; розробка принципів календарного планування виробництва і вирівнювання зайнятості в умовах нестабильного попиту на продукцію; складання календарних планів поточного та капітального ремонту устаткування та його заміни; формування послідовності розвитку комерційної операції і т.д.

Розглянемо деякий керований процес. Припустимо, що керування можна розбити на п кроків, тобто рішення приймається послідовно на кожному кроці, а процедура, яка переводить систему з початкового стану в кінцевий, є сукупністю п покрокових керувань. В результаті керування система переходить із стану S₀b S„.

Позначимо через x_keU_k керування на к-му кроці (к= 1,п), де U_k - множина допустимих керувань на к-му кроці.

Нехай х = (х₁,х₂,...,х_п) - керування, яке переводить систему з

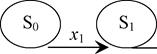
стану S₀ в S_n. Позначимо через S_k стан системи після к-го кроку керування. Отримуємо послідовність станів S₀,S₁,...,S_k_₁,S_k,S_k+1,...,S_n

(рис.7.1.1).

Рисунок 8.1. Схематичне зображення процесу керування

Показник ефективності процесу керування залежить від початкового стану системи і керованої змінної:

Z = F(S₀,x). (8.1)

Власне, задача динамічного програмування формулюється

таким чином: знайти таке значения керованої змінної х\ яке переводить систему з початкового стану S₀ в кінцевий S„, при якому цільова функція (7.1) набуває найбільшого (найменшого) значения.

Розглянемо характерні особливості математичної моделі динамічного програмування:

1) задача оптимізації формулюється як скінчений багатокроковий процес управління;

2) цільова функція (7.1) є адитивною від показника ефективності кожного кроку, тобто виграш від всієї операції складається з виграшів, отриманих на кожному кроці.

п

Z = F(S₀,x) = Y_JF_k(S_k__l,x_k), (8.2)

к=\

де F_k(S_k__l9x_k) = Z_k- показник ефективності на к-му кроці;

3) вибір керування х_кна кожному кроці залежить тільки від стану системи до цього кроку і не впливає на попередні кроки (немає зворотного зв’язку);

4) стан системи S_k після кожного кроку керування залежить тільки від попереднього стану системи S_k.j iкеруючої дії х_k на &-му кроці та не залежить від попередніх станів системи і керувань (відсутність післядії):

S_k=<p_k(S_k__l,x_k), к= 1,п,(8.3)

де (р_к - оператор переходу;

5) на кожному кроці керування х_кзалежить від скінченого числа керованих змінних, а стан системи S_k залежить від скінченого числа параметрів;

6) оптимальним керуванням є вектор х , який знаходиться шляхом послідовних оптимальних покрокових керувань:

х* =(xl,x*₂,...,x*_k,...,x*_n), кількість яких і визначає число кроків

задачі.