ВИДИ ВЗАЄМОЗВ’ЯЗКІВ І ЇХ ОСОБЛИВОСТІ
| Факторна ознака хі | Результативна ознака у за наявності зв’язку | ||
| функціонального | стохастичного | кореляційного | |
| х1 | у1 | у1 у2 | 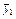
|
| х2 | у2 | у1 у2 у3 | 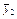
|
| х3 | у3 | у2 у3 у4 | 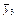
|
| ... | ... | ... | ... |
| хm | уm | уm – 1 уm | 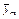
|
Наявність стохастичного зв’язку можна виявити, скориставшись комбінаційним розподілом елементів сукупності. Такий розподіл наведено в табл. 7.2. Сукупність шахт регіону поділено на групи за двома ознаками: х — глибиною розробки вугільних пластів і у — фондомісткістю видобутку вугілля. Кожна група за глибиною розробки пласта характеризується своїм особливим розподілом шахт за фондомісткістю видобутку вугілля. Це умовні розподіли. Порівняння умовних розподілів указує на тенденцію підвищення фондомісткості зі зростанням глибини розробки пластів. Звичайно, для кожної окремої шахти така залежність може не виявитись через вплив інших факторів. Певні межі варіації фондомісткості характерні для кожної групи. Так, на шахтах, де глибина розробки пластів 500 ¼ 700 м, фондомісткість коливається в межах від 18 до 26 грн. за тонну. Проте середній рівень фондомісткості в цій групі вищий порівняно з попередньою групою (300 ¼ 500 м) і нижчий порівняно з наступною (700 і більше):
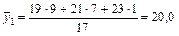 ;
;
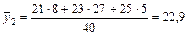 ;
;
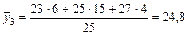 ;
;
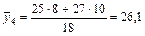 .
.
Середні рівні фондомісткості видобутку вугілля наведено в останній графі таблиці. Зростання групових середніх від групи до групи свідчить про наявність кореляційного зв’язку між глибиною розробки пласта і фондомісткістю вугілля. Отже, кореляційний зв’язок, як і стохастичний, — це властивість сукупності в цілому, а не окремих її елементів.
Таблиця 7.2
КОМБІНАЦІЙНИЙ РОЗПОДІЛ ШАХТ ЗА ГЛИБИНОЮ
РОЗРОБКИ ПЛАСТІВ ТА ФОНДОМІСТКІСТЮ ВУГІЛЛЯ
| Глибина розробки пласта, м | Кількість шахт з рівнем фондомісткості, грн. / т | Середній рівень фондомісткості, грн. / т | |||||
| До 20 | 20—22 | 22—24 | 24—26 | 26 і більше | Разом | ||
| До 300 | 20,0 | ||||||
| 300—500 | 22,9 | ||||||
| 500—700 | 24,8 | ||||||
| 700 і більше | 26,1 | ||||||
| По сукупності в цілому | 23,5 |
Отже, можна не лише стверджувати, що існує кореляційний зв’язок між факторною х і результативною у ознаками, а й визначати, як у середньому змінюється у зі зміною х на одиницю. Ефекти впливу х на у визначаються відношенням приростів середніх групових цих величин 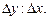 Наприклад, у другій групі порівняно з першою глибина розробки вугільного пласта більша на 200 м, а фондомісткість видобутку вугілля на 22,9 – 20,0 = 2,9 грн. / т. Звідси
Наприклад, у другій групі порівняно з першою глибина розробки вугільного пласта більша на 200 м, а фондомісткість видобутку вугілля на 22,9 – 20,0 = 2,9 грн. / т. Звідси
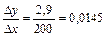 .
.
Тобто, зі зростанням глибини розробки пласта на 100 м фондомісткість зростає в середньому на 1,45 грн. / т.
Аналогічно розраховані ефекти впливу глибини розробки пласта на фондомісткість вугілля у третій групі становлять 0,95, у четвертій — 0,65 грн. на тонну вугілля.
6.2. Кореляційно-регресійний аналіз
Важливою характеристикою кореляційного зв’язку є лінія регресії — емпірична в моделі аналітичного групування і теоретична в моделі регресійного аналізу. Емпірична лінія регресії представлена груповими середніми результативної ознаки 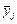 , кожна з яких належить до відповідного інтервалу значень групувального фактора хj. Теоретична лінія регресії описується певною функцією
, кожна з яких належить до відповідного інтервалу значень групувального фактора хj. Теоретична лінія регресії описується певною функцією 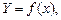 яку називають рівнянням регресії, а Y — теоретичним рівнем результативної ознаки.
яку називають рівнянням регресії, а Y — теоретичним рівнем результативної ознаки.
На відміну від емпіричної, теоретична лінія регресії неперервна. Так, уважають, що маса дорослої людини в кілограмах має бути на 100 одиниць менша за її зріст у сантиметрах. Співвідношення між масою і зростом можна записати у вигляді рівняння: 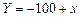 , де у — маса; х — зріст.
, де у — маса; х — зріст.
Безперечно, така форма зв’язку між масою та зростом людини надто спрощена. Насправді збільшення маси не жорстко пропорційне до збільшення зросту. Люди одного зросту мають різну масу, проте в середньому зі збільшенням зросту маса зростає. Для точнішого відображення зв’язку між цими ознаками в рівняння слід увести другий параметр, який був би коефіцієнтом пропорційності при х, тобто Y = – 100 + bx.
Рівняння регресії в такому вигляді описує числове співвідношення варіації ознак х і у в середньому. Коефіцієнт пропорційності при цьому відіграє визначальну роль. Він показує, на скільки одиниць у середньому змінюється у зі зміною х на одиницю. У разі прямого зв’язку b — величина додатна, у разі оберненого — від’ємна.
Подаючи у як функцію х, тим самим абстрагуються від множинності причин, штучно спрощуючи механізм формування варіації у. Аналіз причинних комплексів здійснюється за допомогою множинної регресії.
Різні явища по-різному реагують на зміну факторів. Для того щоб відобразити характерні особливості зв’язку конкретних явищ, статистика використовує різні за функціональним видом регресійні рівняння. Якщо зі зміною фактора х результат у змінюється більш-менш рівномірно, такий зв’язок описується лінійною функцією Y = a + bx. Коли йдеться про нерівномірне співвідношення варіацій взаємозв’язаних ознак (наприклад, коли прирости значень у зі зміною х прискорені чи сповільнені або напрям зв’язку змінюється), застосовують нелінійні регресії, зокрема:
степеневу 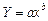 ;
;
гіперболічну 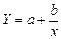 ;
;
параболічну 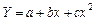 тощо.
тощо.
Вибір та обґрунтування функціонального виду регресії ґрунтується на теоретичному аналізі суті зв’язку. Нехай вивчається зв’язок між урожайністю та кількістю опадів. Надто мала і надто велика кількість опадів спричинюють зниження врожайності, максимальний її рівень можливий за умови оптимальної кількості опадів, тобто зі збільшенням факторної ознаки (опади) урожайність спершу зростає, а потім зменшується. Залежність такого роду описується параболою Y = a + bx + cx2.
Вивчаючи зв’язок між собівартістю у та обсягом продукції х, використовують рівняння гіперболи 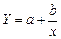 , де а — пропорційні витрати на одиницю продукції, b — постійні витрати на весь випуск.
, де а — пропорційні витрати на одиницю продукції, b — постійні витрати на весь випуск.
Зауважимо, що теоретичний аналіз суті зв’язку, хоча й дуже важливий, лише окреслює особливості форми регресії і не може точно визначити її функціонального виду. До того ж у конкретних умовах простору і часу межі варіації взаємозв’язаних ознак х і у значно вужчі за теоретично можливі. І якщо кривина регресії невелика, то в межах фактичної варіації ознак зв’язок між ними досить точно описується лінійною функцією. Цим значною мірою пояснюється широке застосування лінійних рівнянь регресії:
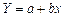 .
.
Параметр b (коефіцієнт регресії) — величина іменована, має розмірність результативної ознаки і розглядається як ефект впливу x на y. Параметр a — вільний член рівняння регресії, це значення y при x = 0. Якщо межі варіації x не містять нуля, то цей параметр має лише розрахункове значення.
Параметри рівняння регресії визначаються методом найменших квадратів, основна умова якого — мінімізація суми квадратів відхилень емпіричних значень y від теоретичних Y:
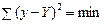 .
.
Математично доведено, що значення параметрів a та b, при яких мінімізується сума квадратів відхилень, визначаються із системи нормальних рівнянь:
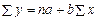 ,
,
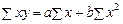 .
.
Розв’язавши цю систему, знаходимо такі значення параметрів:
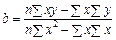 ,
,
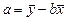 .
.
Розглянемо порядок обчислення параметрів лінійної регресії на прикладі зв’язку між урожайністю зернових і кількістю внесених добрив (у центнерах діючої поживної речовини — д. р.). Значення взаємозв’язаних ознак та необхідні для розрахунку параметрів величини наведено в табл. 7.3.
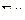 = 12;
= 12; 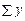 = 224;
= 224; 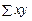 = 342,8;
= 342,8; 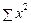 = 18,68;
= 18,68;
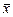 = 12 : 8 = 1,5;
= 12 : 8 = 1,5; 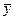 = 224 : 8 = 28.
= 224 : 8 = 28.
Таблиця 7.3
ДО РОЗРАХУНКУ ПАРАМЕТРІВ ЛІНІЙНОЇ РЕГРЕСІЇ,
ТЕОРЕТИЧНИХ РІВНІВ І ЗАЛИШКОВИХ ВЕЛИЧИН
| Номер господар- ства | Кількість внесених добрив х, д. р | Урожайність зернових у, ц/га | ху | х2 | Y | y – Y | (y – Y)2 |
| 1,1 | 25,3 | 1,21 | –1 | ||||
| 1,4 | 35,0 | 1,96 | –2 | ||||
| 1,2 | 31,2 | 1,44 | |||||
| 2,0 | 66,0 | 4,00 | |||||
| 1,5 | 40,5 | 2,25 | –1 | ||||
| 1,3 | 2,8 | 36,4 | 1,69 | ||||
| 1,8 | 54,0 | 3,24 | –1 | ||||
| 1,7 | 54,4 | 2,89 | |||||
| Разом | 12,0 | 342,8 | 18,68 | ´ |
Користуючись цими величинами, визначаємо:
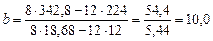 (ц/га);
(ц/га);
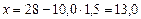 .
.
Отже, рівняння регресії має вигляд
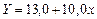 ,
,
тобто кожний центнер внесених добрив (у перерахунку на діючу поживну речовину) дає приріст урожайності в середньому 10 ц/га. Якщо добрива зовсім не вносити (х = 0), то урожайність зернових не перевищить 13,0 ц/га.
Рівняння регресії відбиває закон зв’язку між х і у не для окремих елементів сукупності, а для сукупності в цілому; закон, який абстрагує вплив інших факторів, виходить з принципу «за інших однакових умов». За цих умов очікувана врожайність зернових при внесенні добрив у обсязі 1,1 ц д. р. на 1 га становить Y = 13 + 10 × 1,1 = 24 (ц/га). Для інших значень факторної ознаки х теоретичні рівні врожайності наведено в табл. 7.3. Вплив інших окрім х факторів зумовлює відхилення емпіричних значень у від теоретичних у той чи інший бік. Відхилення (y – Y) називають залишками і позначають символом е. Залишки, як правило, менші за відхилення від середньої, тобто 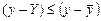 .
.
У нашому прикладі
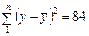 ,
, 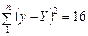 .
.
Відповідно загальна дисперсія врожайності
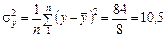 ,
,
Дата добавления: 2016-07-27; просмотров: 2733;











