Лекция 8. Построение математических моделей
План лекции:
1 Способы обобщения результатов, полученных в ходе проведения исследования.
2 Выражение опытных закономерностей в виде формул
3 Установление информационной ценности математической модели
4 Проверка адекватности описания математической моделью экспериментальных данных
Способы обобщения результатов, полученных в ходе проведения исследования
Для универсального оперирования полученной информацией необходимо обобщать экспериментально полученные данные до уровня математического абстрагирования. Обобщение результатов эксперимента, полученных в различных опытах, проводят при помощи вычисления величин: М - среднее арифметическое, 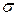 - среднеквадратическое отклонение, Сv - коэффициент вариации, которые удобно выражать через моменты h-го распределения -
- среднеквадратическое отклонение, Сv - коэффициент вариации, которые удобно выражать через моменты h-го распределения - 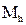 , а степень их достоверности через величину ошибки репрезентативности -
, а степень их достоверности через величину ошибки репрезентативности - 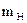 (см приложение, табл.1.). Необходимым условием правомерности использования этих параметров является нормальность распределения изучаемых выборок, критериями, определения которых служат: коэффициент асимметрии распределения - As и коэффициент эксцесса - Ех. Для избежания получения искажения объективной информации также необходимо исключить грубые ошибки, которые возникают при проведении измерений. Численным показателем достоверности текущего значения - хi, а также достоверности конкретной выборки - tp, является критерий Стьюдента - tst(p,n).
(см приложение, табл.1.). Необходимым условием правомерности использования этих параметров является нормальность распределения изучаемых выборок, критериями, определения которых служат: коэффициент асимметрии распределения - As и коэффициент эксцесса - Ех. Для избежания получения искажения объективной информации также необходимо исключить грубые ошибки, которые возникают при проведении измерений. Численным показателем достоверности текущего значения - хi, а также достоверности конкретной выборки - tp, является критерий Стьюдента - tst(p,n).
В случае, если исследователь наблюдает расхождение двух величин целевых функций С, полученных при измерении изучаемых факторов аi, то достоверность данного расхождения можно подтвердить при помощи критерия Стьюдента - td. Общим принципом чистоты проведения исследования является постоянство всех остальных факторов при изменении избранных aj. Тестом на соблюдение выше приведенного условия является критерий равноточности измерений. Равноточность измерений серии опытов позволяет обобщить результаты различных экспериментов и уменьшить суммарные ошибки исследования. Показателем равноточности опытов является критерий Фишера - F.
Далее экспериментальные данные обобщают в такой последовательности: находят функциональные связи изучаемых явлений, устанавливают основные закономерности, математически выражают, раскрывают их физическую сущность с целью последующего теоретического развития.
Вывод эмпирических формул проводится на основе экспериментально полученной функциональной зависимости, объясняемой в общем, виде. Подбор типа эмпирической формулы для определения ее параметров используется на основе регрессионного анализа. Построение регрессионной зависимости осуществляется при помощи использования специальных прикладных программ, разработанных на ЭВМ. Полученное эмпирическое выражение можно представить в полуаналитическом или чисто аналитическом виде. Иногда сама структура эмпирической формы указывают на пути превращения в аналитическую формулу. Под аналитическими уравнениями следует понимать такие, в которых все основные члены имеют размерность и логично вытекают из законов физики.
Наличие аналитического выражения зависимости целевой функции от ее аргументов, позволяет использовать его как математическую модель. Очевидно, что исследование считается законченным, если достигнута его цель. Если реализация цели заключена в нахождении максимальной или минимальной величины целевой функции, то построение математической модели, отражающей природу взаимосвязи между целевой функцией С и ее аргументами аi, вi и di, является наиболее приемлемым способом нахождения оптимальных значений изучаемых факторов аi, Смак= F(аiопт, вi). Математические модели строятся на основе полученных эмпирических и рациональных формул, а поэтому их удобно разделять на описательные и объяснительные.
Математические модели являются мощным инструментом, как описания так и анализа полученных данных. Ценность модели определяется степенью адекватности описания изучаемых явления и возможностью их объяснения. Математическое абстрагирование полученных результатов способствует разрешению проблемы не повторяемости экспериментальных данных при изменяющихся условиях проведения опытов и служит отправным моментом проведения дальнейших исследований.
Наиболее ярким примером значимости математического моделирования в решении прикладных задач являться работа П. Мейзура [16]. Благодаря данной модели впервые удалось получить жизнеспособное потомство от деконсервированных эмбрионов млекопитающих после неудачно проведенных эмпирических поисков на протяжении трех десятилетий.
Повышение эффективности исследовательской работы связано с моделированием проведения эксперимента от постановки задачи на исследования до математического обобщения полученного результата. Предложенная структурная схема моделирования эксперимента, позволяет получать достоверный научный результат при минимальных затратах времени и средств.
Выражение опытных закономерностей в виде формул
1) Вывод эмпирических формул:
Для вывода эмпирических формул необходимо иметь экспериментально полученную функциональную зависимость, объясняемую в общем виде. Основной метод построения эмпирических формул: подбор типа формулы и нахождение коэффициентов к ней. Подбор типа формулы главное, что определяет результативность и точность эмпирической формулы. Следует учесть также, что кривая изменения функции часто может быть представлена несколькими типами уравнений. В этих случаях надо выбирать такой тип формулы, который в наибольшей мере соответствовал бы природе явлений и мог бы быть улучшен превращением формулы в полуэмпирическую или полурациональную.
Подбор типа эмпирической формулы для определения ее параметров используется на основе регрессионного анализа. Параметры формулы надо вычислять с достаточной степенью точности, особенно, если они относятся к показателям степени. Не надо забывать, что многие математические выражения закономерности, будучи вначале эмпирическими, впоследствии были рационализированы и что иногда сама структура эмпирической формы указывает на пути превращения ее в формулу рациональную.
2) Получение рациональных формул:
Под рациональными формулами следует понимать такие, в которых все основные члены имеют размеренность и строго логично вытекают из законов физики. Рациональные формулы не только представляют собой закономерность развития явления, но и объясняют его (хотя бы и в общей форме), показывая факторы и связи между ними. Это важнейший тип формул, так как их всеобщность дает возможность теоретически исследовать все стороны явления.
Для построения рациональной формулы необходимо знать физические основы явления. Не следует увлекаться непродуманными математическими обобщениями. Надо всегда помнить как о необходимости в связи формул с реальными физическими процессами, так и о возможной ограниченности их приложения. Для выведения рациональной формулы вначале следует установить, какой закон или законы физики применимы для объяснения явления. Затем следует решить вопрос о том, какой трансформации или дополнений требуют известные уже выражения законов в связи с особенностями развития явления. Далее решают, как лучше в общей и грубой схеме математически представить найденные зависимости. Наконец, эту схему уточняют, “отшлифовывают” и проверяют на ряде примеров.
Развитие явления обычно может быть представлено дифференциальными уравнениями. При преобразовании первоначальных математических схем в дифференциальные уравнения следует стремиться к простым и ясным выражениям; это предлагает соответствующий выбор системы отсчета (координат), решения вопроса о порядках уравнения и о том, могут ли быть коэффициенты уравнений постоянными величинами.
Не всегда исследователю удается обогатить науку открытием новых рациональных формул. В ряде случаев бывает полезно представить конкретную экспериментальную кривую, описывая ее чисто математически и преимущественно безразмерными величинами. Такие формулы называются эмпирическими. Они не имеют характера всеобщности, а показывают развитие явления только для условий, в которых проводились опыты. Наличие аналитического выражения зависимости целевой функции от ее аргументов, позволяют использовать его как математическую модель.
Очевидно, что исследование считается законченным, если реализована его цель. Поскольку реализация цели заключена в нахождении максимальной или минимальной величины целевой функции, то построение математической модели, отражающей природу взаимосвязи между целевой функцией С и ее аргументами аi , вi и di, является наиболее приемлемым способом: С мак = F (а iопт, вi ).
Математические модели строятся на основе полученных эмпирических и рациональных формул, а поэтому их удобно разделять на описательные и объяснительные. В англоязычной литературе - выделяют модели феноменологические и механистические, критериями состоятельности которых являются информационная ценность и адекватность описания изучаемых явлений [15].
Установление информационной ценности математической модели
Для проверки информационнойценности модели формулируется нуль-гипотеза Н0: 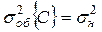 , где -
, где - 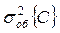 , общее рассеивание результатов измерений по отношению к общему среднему по всему эксперименту.
, общее рассеивание результатов измерений по отношению к общему среднему по всему эксперименту. 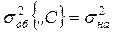 - рассеивание средних экспериментальных значений выходов
- рассеивание средних экспериментальных значений выходов 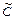 от предсказываемых моделью значений
от предсказываемых моделью значений 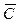 . Эта величина характеризует неадекватность описания модели эксперимента.
. Эта величина характеризует неадекватность описания модели эксперимента.
Если 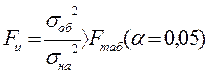 (24),
(24),
то модель (имеющая 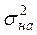
 ) описывает результаты эксперимента лучше, чем простейшая модель. Если Fu < Fтабл , то такая модель, несмотря на сложный вид и на ее построение, не имеет информационной ценности.
) описывает результаты эксперимента лучше, чем простейшая модель. Если Fu < Fтабл , то такая модель, несмотря на сложный вид и на ее построение, не имеет информационной ценности.
Проверка адекватности описания математической моделью экспериментальных данных
Для проверки адекватности модели формируется нуль-гипотеза Н0:
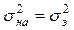 . Если она по критерию Фишера (см. приложение, табл. 3) Fа:
. Если она по критерию Фишера (см. приложение, табл. 3) Fа:
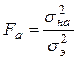 (24а),
(24а),
будет признана правдоподобной (F а<Fтабл обычно при a=0,05), то анализируемая модель адекватно описывает экспериментальные результаты, поскольку 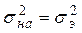 , и предсказываемые моделью результаты
, и предсказываемые моделью результаты 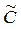 будут по точности не хуже экспериментальных.
будут по точности не хуже экспериментальных.
Существуют и другие способы проверки полученных математических моделей. Выверенные модели позволяют получить объективную информацию с тем же уровнем надежности с которым они протестированы. Однако не следует забывать, что хотя аналитическое представление и сам анализ полученных результатов в ходе исследования является самым универсальным способом, но полученные выводы верны с той степенью надежности и при тех условиях, при которых они были получены. Дальнейшее обобщение полученных модельных результатов необходимо проводить с большой осторожностью.
Далеко не перед каждым исследователемпредстает необходимость проводить работу в такой последовательности и объеме, как изложено выше, а именно, от постановки задачи до получения результатов математического моделирования. Однако большая часть проблем, затронутых в данной работе, так или иначе, станут актуальными при проведении любого, даже самого простого эксперимента. Многолетний опыт работы в области биотехнологии, где особенно требуется применение комплексных методов исследования и его обобщение, позволил создать выше приведенный алгоритм проведения работы.
Вопросы для самоконтроля.
1 Перечислите основные способы обобщения результатов, полученных в ходе проведения исследования.
2 Какова необходимость получения математических моделей?
3 Охарактеризуйте процедуру получения эмпирических формул.
4 В чем заключено основное отличие эмпирических формул от рациональных?
5 Как производится установление информационной ценности математической модели?
6 Как производится проверка адекватности описания математической моделью экспериментальных данных
Приложение
1. Структурная схема проведения биологического исследования

2. Получение основных статистических параметров и критериев их достоверности
Таблица 1. Получение основных статистических параметров и критериев их достоверности, выраженных через моменты распределения
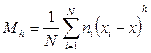 - момент h-го распределения. - момент h-го распределения.
| 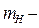 ошибка репрезентативности. ошибка репрезентативности.
| tst(p,n) - критерий Стьюдента (критерий достоверности). |
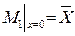 - среднее арифметическое. - среднее арифметическое.
| 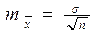
| 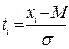 - текущего значения. Если ti>3, то хi- не принадлежит данной выборке. - текущего значения. Если ti>3, то хi- не принадлежит данной выборке.
|
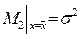 - дисперсия. - дисперсия.
| 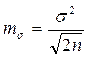
| |
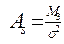  (0,2<As<0,5) - коэффициент асимметрии. (0,2<As<0,5) - коэффициент асимметрии.
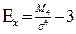 - коэффициент эксцесса. ( - коэффициент эксцесса. ( 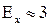 - условие нормальности распределения). - условие нормальности распределения).
| 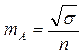
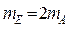
| 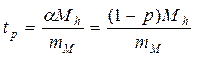 - достоверность конкретной выборки. Если - достоверность конкретной выборки. Если 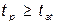 , то Н0=0 данное распределение. , то Н0=0 данное распределение.
|
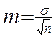 - статистическая ошибка. - статистическая ошибка.
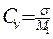 - коэффициент вариации. - коэффициент вариации.
| 
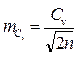
| Принадлежит генеральному, при заданном уровне надёжности - р ( 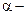 уровень значимости выборки). уровень значимости выборки).
|
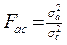 - критерий Фишера. - критерий Фишера.
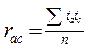 - коэффициент корреляции. - коэффициент корреляции.
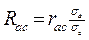 - коэффициент регрессии - коэффициент регрессии
|
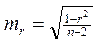
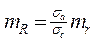
| 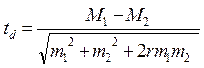 - достоверность различия двух выборок.
Если - достоверность различия двух выборок.
Если 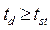 , то , то  - данные распределения не принадлежат генеральному. - данные распределения не принадлежат генеральному.
|
Примечание: Н0 - нулевая гипотеза, (предполагает принадлежность данного распределения генеральному Н0=0).
3. Табличные данные критерия Стьюдента
Таблица 2. Значения коэффициента Стьюдента(t -распределение)
| \ Р k \ | 0,95 | 0,99 | 0,999 |
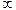
| 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,179 2,145 2,120 2,101 2,086 2,074 2,064 2,056 2,048 2,042 2,021 2,000 1,980 1,960 | 9,925 5,841 4,604 4,032 3,707 3,499 3,355 3,250 3,169 3,055 2,977 2,921 2,878 2,845 2,819 2,797 2,779 2,763 2,750 2,704 2,660 2,617 2,576 | 31,598 12,924 8,610 5,959 5,408 5,041 4,781 4,587 4,318 4,140 4,015 3,922 3,850 3,792 3,745 3,707 3,674 3,646 3,551 3,460 3,373 3,291 |
Примечание: k - число степеней свобод. Для нахождения критерия Стьюдента, в случае одной выборки tp, k=n-1. Для  установления достоверности различия двух выборок td, k=n1+n2-2.
установления достоверности различия двух выборок td, k=n1+n2-2.
4. Табличные данные критерия Фишера
Таблица 3. Значения критерия Фишера (F-распределение)
| \N1N2\ | ||||||||||||
| 9,0 9,0 9,5 30,8 6,9 18,0 5,8 13,3 5,1 10,9 4,7 9,6 4,5 8,6 4,3 8,0 4,1 7,6 3,5 5,9 3,2 5,2 3,2 4,5 | 9,2 9,2 9,3 29,5 6,6 16,7 5,4 12,1 4,8 9,8 4,4 8,5 4,1 7,6 3,9 7,0 3,7 6,6 3,1 4,9 2,8 4,3 2,7 4,1 | 9,3 9,3 9,1 8,7 6,4 6,0 5,2 1,4 4,5 9,2 4,1 7,6 3,8 7,0 3,6 6,4 3,5 6,0 2,8 4,4 2,6 3,8 2,5 3,7 | 9,3 9,3 9,0 28,2 6,3 15,5 5,1 11,0 4,4 8,8 4,0 7,5 3,7 6,6 3,5 6,1 3,3 5,6 2,7 4,1 2,5 3,5 2,4 3,3 | 9,3 9,3 8,9 27,9 6,2 15,2 4,9 10,7 4,3 8,5 3,9 7,2 3,6 6,4 3,4 5,8 3,2 5,4 2,6 3,9 2,3 3,3 2,3 3,1 | 9,3 9,4 8,9 27,7 6,1 15,0 4,9 10,5 4,2 8,3 3,8 7,0 3,5 6,2 3,3 5,6 3,1 5,2 2,5 3,7 2,3 3,1 2,2 3,0 | 9,4 9,4 8,9 27,5 6,1 14,8 4,8 10,3 4,2 8,1 3,7 6,8 3,4 6,0 3,2 5,5 3,1 5,1 2,5 3,6 2,2 3,0 2,1 2,8 | 9,4 9,4 8,8 27,4 6,0 14,7 4,8 10,2 4,1 8,0 3,7 6,7 3,4 5,9 3,2 5,4 3,1 4.9 2,4 3,5 2,1 2,9 2,0 2,7 | 9,4 99,4 8,8 27,2 6,0 14,6 4,7 10,1 4,1 7,8 3,6 6,6 3,3 5,8 3.1 5,3 3,0 4,9 2,4 3,4 2,1 2,8 2,0 2,6 | 19,5 99,5 8,7 26,7 5,8 14,0 4,6 9,6 3,9 7,4 3,4 6,2 3,1 5,4 2,9 4,8 2,8 4,4 2,1 2,9 1,8 2,4 1,8 2,2 | 19,5 99,5 8,6 26,4 5,7 13,8 4,5 9,3 3,8 7,1 3,3 5,9 3,0 5,1 2,8 4,6 2,7 4,2 2,0 2,7 1,7 2,1 1,7 1,9 | 9,5 99,5 8,6 26,3 5,7 13,7 4,4 9,2 3,7 7,1 3,3 5,8 3,0 5,0 2,8 4,5 2,6 4,1 2,0 2,6 1,6 2,0 1,6 1,8 |
Примечание: верхний ряд - при P=0,95, нижний - при P=0,99.
Примеры
Пример 1.Установить основные статистические величины для представленных выборок с уровнем надежности Р=0,95 и Р=0,99.
А) Количественный метод. Измерение силы тока в первой выборке составило: 28,8; 26,3; 31,4; 26,4; 27,4; 29,4; 25,1 мкА. Во второй выборке измерения силы тока составило: 32,8; 37,4; 36,6; 37,1; 42,3; 33,4; 28,9; 37,6 мкА.
Б) Качественный метод - альтернативного варьирования. Определить величину сохранности биообъекта С % в каждой из представленных выборок. Общее количество биообъекта в первой выборке составляет n1=56 и во второй n2=66. Количество биообъекта, которое сохранило заданное качество в первой выборке n01=36, а другой n02=48.
Решение:
А) Количественный метод.
1) Определим наличие грубых ошибок.
а) Для первой выборки: 25,1; 26,3; 26,4; 27,4; 28,8; 29,4; 31,4; n1=7.
б) Для второй: 28,9; 32,8; 33,4; 36,6; 37,1; 37,4; 37,6; 42,3; n2=8.
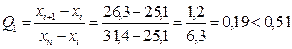 ;
; 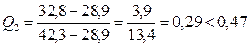 .
.
Вывод - грубых ошибок нет.
Дата добавления: 2020-10-14; просмотров: 637;











