Вычислим средние величины по каждой из представленных выборок.
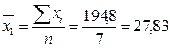 ;
;  .
.
3) Установим величины среднеквадратического отклонения
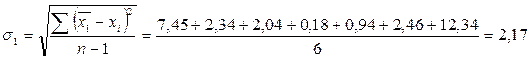 ;
;
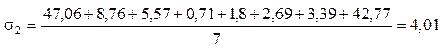 ;
;
Вывод - измерения неравноточные.
4) Определим коэффициенты вариации наших выборок
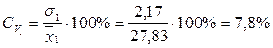 - вариабельность средняя;
- вариабельность средняя;
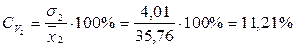 - вариабельность высокая.
- вариабельность высокая.
5) Установим величины ошибок среднеквадратического отклонения
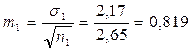 ;
; 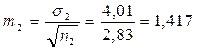 .
.
6) Оценим величины доверительных интервалов при различных уровнях надежности (при Р=0,95 t=2,16 и Р=0,99 t=3,02).
а) для уровня надежности Р=0,95:
 ;
; 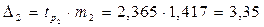 .
.
б) для уровня надежности Р=0,99:
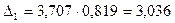 ;
; 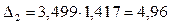 .
.
7) Установим относительные ошибки измерения (уровень значимости оценки достоверности) для различных уровней надежности Р=0,95 и Р=0,99.
а) для уровня надежности Р=0,95:
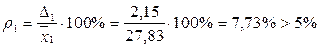 ;
; 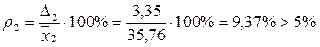 .
.
б) для уровня надежности Р=0,99:
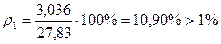 ;
; 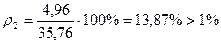 .
.
Вывод - необходимо большее число измерений.
8) Установим минимальное количество измерений в каждой из выборок.
а) для уровня надежности Р=0,95:
 ;
; 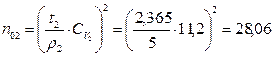 .
.
б) для уровня надежности Р=0,99:
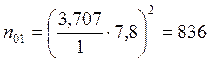 ;
; 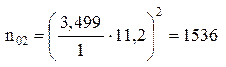 .
.
Б) Качественный -метод альтернативного варьирования.
1) Установим показатели вероятности для каждой из выборок.
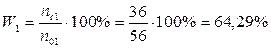 ;
; 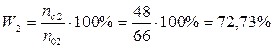 .
.
2) Вычислим среднеквадратическое отклонение.
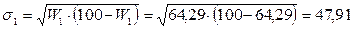 ;
; 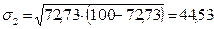 .
.
Вывод - измерения неравноточные.
3) Определим коэффициенты вариации.
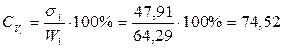 - высокая вариабельность,
- высокая вариабельность,
 - высокая вариабельность.
- высокая вариабельность.
4) Оценим ошибки среднеквадратического отклонения.
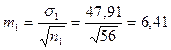 ;
; 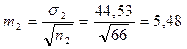 .
.
5) Оценим величины доверительных интервалов при различных уровнях надежности.
а) для уровня надежности Р=0,95:
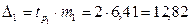 ;
; 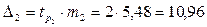 .
.
б) для уровня надежности Р=0,99:
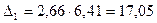 ;
; 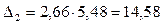 .
.
6) Установим относительные ошибки измерения (уровень значимости оценки достоверности) для различных уровней надежности Р=0,95 и Р=0,99.
а) для уровня надежности Р=0,95:
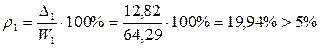 ;
; 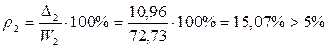 .
.
б) для уровня надежности Р=0,99:
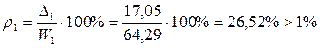 ;
; 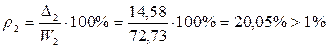 .
.
Вывод - необходимо увеличить количество измерений.
7) Установим минимальное количество измерений в каждой из выборок.
а) для уровня надежности Р=0,95:
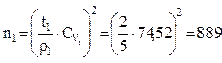 ;
;  .
.
б) для уровня надежности Р=0,99:
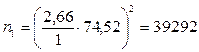 ;
;  .
.
Пример 2.Установить достоверность различия сравниваемых выборок с уровнем надежности Р=0,95 и Р=0,99.
А) Количественный метод. Измерение силы тока в первой выборке составило: 27,8; 28,3; 31,4; 26,4; 29,4; 24,4; 27,1 мкА. Во второй выборке измерения силы тока составило: 32,8; 37,4; 36,6; 38,1; 41,3; 32,4; 28,9; 39,6 мкА.
Б) Качественный метод - альтернативного варьирования. Определить величину сохранности биообъекта (С %) в каждой из представленных выборок. Общее количество биообъекта в первой выборке составляет n1=66 и во второй n2=78. Количество биообъекта, которое сохранило заданное качество в первой выборке n01=23 и во второй n02=25.
Решение:
А) Количественный метод.
1) Определим наличие грубых ошибок.
а) Для первой выборки: 24,4; 26,4; 27,1; 27,8; 28,3; 29,4; 31,4.
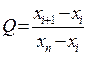 ;
; 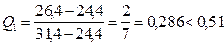 ;
; 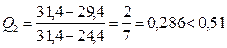 .
.
Вывод - первая выборка не имеет грубых ошибок.
б) Для второй: 28,9; 32,4; 32,8; 36,6; 37,4; 38,1; 39,6; 41,3.
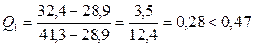 ;
; 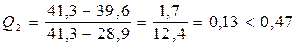 .
.
Вывод - вторая выборка не имеет грубых ошибок.
2) Вычислим средние величины по каждой из представленных выборок.
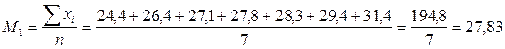 ;
;
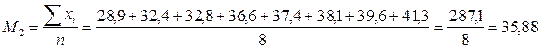 .
.
3) Установим величины среднеквадратического отклонения.
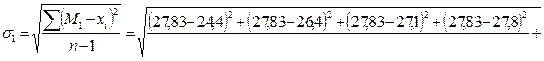
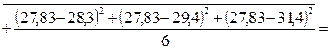
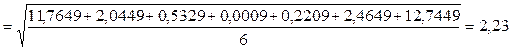
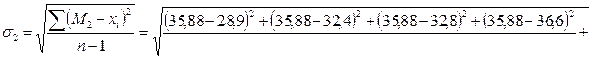
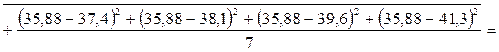
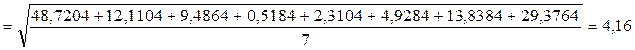
4) Определим коэффициенты вариации наших выборок.
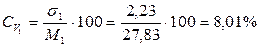 ;
; 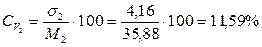 .
.
Дата добавления: 2020-10-14; просмотров: 609;











