Рівняння руху механізму

Для визначення законів руху початкових ланок за заданими силами використовуються рівняння, що називаються рівняннями руху механізму. Число цих рівнянь дорівнює числу ступенів рухомості механізму.

Рівняння руху механізму можуть бути представлені в різних формах. Для механізмів з одним ступенем вільності одна з найпростіших форм рівнянь отримується на основі теореми про зміну кінетичної енергії: зміна кінетичної енергії механізму на деякому переміщенні дорівнює сумі робіт усіх сил, що діють на ланки механізму на цьому самому переміщенні. Цей закон подають у вигляді рівняння

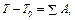(4.9)

де Т – кінетична енергія механізму в довільному положенні; Т₀ – кінетична енергія механізму в положенні, що приймається за початкове; 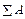– алгебраїчна сума робіт усіх сил і моментів, що прикладені до механізму на деякому переміщенні.

Роботу здійснюють усі активні сили і моменти та сили тертя у всіх кінематичних парах механізму.

Рівняння руху в енергетичній формі. Зведемо усі сили і моменти механізму з одним ступенем вільності до однієї ланки зведення, тобто замінимо розглядуваний механізм його динамічною моделлю. Оскільки все навантаження, прикладене до моделі, виражається зведеним моментом М_ЗВ, то права частина рівняння (4.9) дорівнює

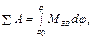(4.10)

а саме рівняння (4.9), враховуючи (4.6) , можна записати у вигляді

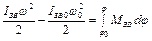. (4.11)

Рівняння (4.11) називають рівнянням руху механізму в енергетичному виді, або – в формі рівняння кінетичної енергії. Загалом верхня межа 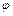інтегрування в (4.11) вважається змінною.

Якщо все навантаження, що прикладене до механізму, залежить тільки від його положення (і не залежить від 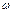), то рівняння (4.10) розв’язується безпосередньо відносно шуканої величини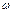

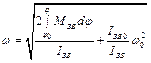. (4.12)

При заданих функціях І_ЗВ, М_ЗВ і відомій швидкості 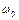в початковий момент, рівняння (4.12) дозволяє визначити значення 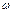при різних переміщеннях ланки зведення. Таким чином можна отримати дійсний закон руху механізму.

Якщо дослідження механізму починається з моменту пуску (тобто 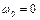), то (4.12) набуде вигляду

.

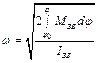Аналогічно (4.11) можна представити рівняння руху механізму, якщо всі сили і маси зводяться до вибраної точки зведення В

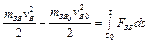. (4.13)

Рівняння руху в диференційній формі. Рівняння руху механізму в енергетичній формі (4.11) використовується, переважно, у випадках коли зведені силові фактори залежать від положень ланок. В інших випадках використовується диференційне рівняння руху механізму, яке можна отримати, продиференціювавши рівняння (4.11) по координаті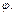

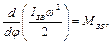
або, враховуючи, що в загальному випадку змінною величиною є не тільки 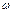, але й І_ЗВ , після нескладних перетворень одержимо

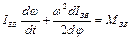. (4.14)

Рівняння (4.14) називається рівнянням руху в диференційній формі, оскільки шукана змінна величина – кутова швидкість 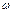початкової ланки, знаходиться під знаком похідної.

У випадку, коли досліджуваний механізм має І_ЗВ=const, то рівняння (4.14) спрощується і має вигляд

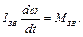
Для визначення кутового прискорення початкової ланки розв’яжемо рівняння (4.14) відносно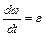

.

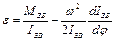Похідна 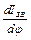обчислюється чисельним диференціюванням на ЕОМ, або графічним диференціюванням, якщо це не можливо зробити аналітично.

Режими руху

Дослідження динаміки машин полягає, в першу чергу, у визначенні та аналізі часткових рішень, наведених вище диференційних рівнянь руху, що відповідають характерним режимам роботи.

Процес руху машини в загальному випадку складається з трьох режимів: розбігу, усталеного руху, вибігу. Це наочно показує діаграма залежності швидкості руху початкової ланки від часу (рис. 4.2). При усталеному русі швидкість головного вала змінюється періодично, інколи вона може бути постійною. Розбіг та вибіг – це перехідні режими, які характеризуються неперіодичними змінами швидкості вала машини (початкової ланки). З цих міркувань часто розрізняють два режими: усталений рух та перехідні процеси.

Усталений рух. Під усталеним рухом будемо розуміти такий режим роботи, при якому вхідний параметр двигуна (параметри u, що керує процесом перетворення енергії) лишається постійним (u=u_о=const), а кутова швидкість вихідного вала двигуна або лишається постійною, або коливається біля деякого середнього значення 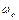, причому найбільші відхилення малі у порівнянні з цим середнім значенням. Іншими словами, в цьому випадку

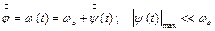. (4.15)

Усталеним рухом машини називається рух, при якому її кінетична енергія є періодичною функцією часу. Проміжок часу (t_ц), протягом якого швидкість головного вала набуває свого початкового значення, пройшовши через 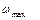та 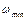, називають циклом усталеного руху.

Оскільки швидкості на початку та в кінці циклу усталеного руху рівні між собою ( 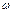_о= 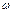), то рівняння руху (4.9) набуває вигляду

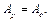
Рівність (4.15) – основне енергетичне рівняння усталеного руху. При усталеному русі робота рушійних сил за один цикл дорівнює роботі сил опору (виробничого та шкідливого). У середині циклу ця рівність, як правило, не зберігається, а тому мають місце коливання швидкості початкових ланок. Якщо, 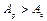- рух механізму прискорений і навпаки.

Перехідні процеси.Розбіг - це режим руху, у процесі якого машина зі стану спокою приходить до усталеного руху.Рівняння руху набуває вигляду

.

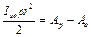Оскільки кінетична енергія завжди додатна, то для можливості пуску машини необхідно, щоб робота рушійних сил була більшою за роботу сил опору, 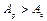. Надлишок роботи А_р витрачається на збільшення кінетичної енергії механізму, тобто збільшення швидкості рухомих мас.

Вибіг(зупинка) – це режим руху, в процесі якого машина переходить від усталеного руху до стану спокою. Переважно при вибігу двигун відключається або переводиться в генераторний режим, при якому вводиться додатковий гальмівний момент.

Таким чином, у період розбігу кінетична енергія машини збільшується за рахунок надлишку роботи рушійних сил над роботою сил опору (А_р>А_о); під час усталеного руху кінетична енергія на початку та в кінці кожного циклу однакова (А_р=А_о); у період вибігу кінетична енергія повністю поглинається роботою сил опору.

Перехідні процеси при зміні навантаження. Часто усталений рух чергується із розбігом (при підвищеннях швидкісного режиму) та гальмуваннями (при зменшенні швидкості). Так працює, наприклад, автомобільний двигун.

Відмітимо, що багато механізмів не працюють у режимі усталеного руху.