Динамічна модель машинного агрегату

Машинний агрегат – це, переважно, сукупність машини-двигуна, механізму передач та робочої машини. Це, як правило, багатоланкова система, навантажена багатьма силами та моментами, прикладеними до різних ланок. На рис. 4.1, як приклад, приведена силова установка, в якій ДВЗ приводить в рух через зубчасту передачу вал робочої машини – відцентрової помпи. До ланок машинного агрегату під час руху прикладені різні сили: рушійна сила F_Д, сила корисного опору – момент М_РМ, сили тяжіння, в усіх кінематичних парах діють сили тертя. Характер дії цих сил різний: деякі залежать від положення чи швидкості ланок, інші постійні. При цьому кожна ланка має свою масу, момент інерції. Своїми діями прикладені сили надають механізму той чи інший закон руху. Визначення закону руху такої складної багатоланкової системи становить непросту задачу.

У той же час для механізму, що має один ступінь вільності, задачу можна вважати розв’язаною, якщо буде відомий закон руху однієї ланки, яка таким чином буде початковою. Закон руху інших ланок і точок механізму після цього можна без значних зусиль визначити методами кінематичного аналізу.

Викладене наводить на думку замінити весь складний багатоланковий механізм однією умовною рухомою ланкою. Виберемо за таку ланку 1 (рис. 4.1, а) та виділимо її разом зі стояком (рис. 4.1, б). До умовної ланки пред’явимо такі вимоги: нехай її момент інерції І_зв і момент сил М_зв, якими вона навантажена, будуть такими, що закон руху умовної ланки буде повністю співпадати з законом руху ланки 1 заданого механізму, тобто для будь-якого моменту часу буде справедливим рівняння ,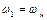

де 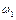- кутова швидкість кривошипу 1 заданого механізму, 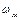- кутова швидкість умовної ланки (моделі).

Це означає, що умовна ланка зі стояком є своєрідною динамічною моделлю машинного агрегату. Таким чином, якщо визначити закон руху цієї простої моделі (рис. 4.1, б), то автоматично стане відомим дійсний закон руху початкової ланки заданого механізму. Зазначимо, якщо заданий механізм має кривошип, то його доцільно вибрати за рухому ланку динамічної моделі.

Підсумуємо викладене. Побудова динамічної моделі машинного агрегату полягає в заміні заданого багатоланкового механізму, навантаженого довільною системою сил та моментів, простою динамічною моделлю (рис. 4.1, б) – однією умовною рухомою ланкою зі стояком. При цьому, всі сили і моменти, що прикладені до заданого механізму, замінені, як правило, одним зведеним моментом, що прикладений до умовної ланки. Отже М_зв є еквівалентом до всього навантаження, прикладеного до машинного агрегату. Так само маси всіх ланок замінені моментом інерції умовної ланки - зведеним моментом інерції І_зв.

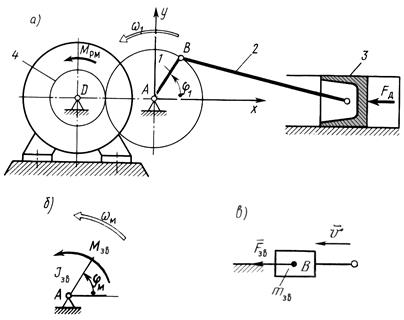
Рис. 4.1

Таким чином, побудова динамічної моделі полягає в зведенні сил – визначенні М_зв і в зведенні мас – визначенні І_зв. При цьому, щоб динамічна модель була адекватна заданому механізму, необхідно (слідує з рівняння Лагранжа ІІ роду, принципу можливих переміщень), щоб при зведенні сил була витримана умова рівності елементарних робіт всіх сил і моментів, прикладених до ланок реального механізму, і зведеної сили; при зведенні мас - умова рівності кінетичних енергій мас реального механізму і зведеного моменту інерції моделі.

Наголосимо: побудова динамічної моделі дає змогу, розв’язуючи задачі динаміки, розглядати не весь складний машинний агрегат з багатьма ланками, що мають різні маси та на які діють різні сили, а одну умовну ланку з однією еквівалентною масою (чи моментом інерції) із прикладеною до неї, як правило, однією силою (чи моментом).

Зазначимо, що в загальному випадку розрізняють дві динамічні моделі: з розподіленою масою (рис. 4.1, б), та із зосередженою масою (рис. 4.1, в). Остання застосовується, переважно, якщо в складі механізму немає жодної ланки, що здійснює обертальний рух.