ЛЕКЦИЯ 2. ОСНОВНЫЕ ЗАКОНЫ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

4. Закон Ома для активной ветви

Активная ветвь, называемая так из-за наличия источника ЭДС, изображена на рис. 2.2.

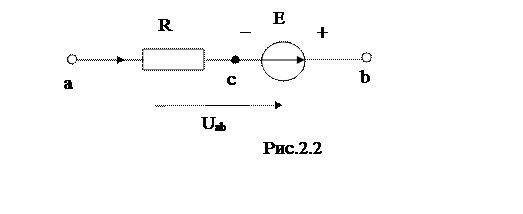
Между выходными зажимами ветви возникает напряжение Uab . Индексация показывает направление ко второму индексу. Напряжение – это разность потенциалов между двумя точками, т. е. Uab =Va −Vb .

Определим потенциал точки a, исходя из потенциала Vb . Рассчитаем

изменение потенциала промежуточной точки с (рис. 2.2) по сравнению с Vb .

Между точками b и c расположен источник ЭДС, поэтому потенциал точки с

отличается от потенциала точки b на величину Е. Стрелка источника показывает направление увеличения потенциала. Следовательно, потенциал точки с ниже потенциала точки b. Между точками с и а находится резистор сопротивлением R. Потенциал Va отличается от потенциала Vc величиной напряжения на резисторе RI . Ток направлен от большего потенциала к меньшему, поэтому потенциал Va выше потенциала Vc .

Таким образом

Va =Vb − E + RI,

Va −Vb = −E + RI.

Но Va −Vb =U_ab , т. е. U_ab = −E + R I .

Можно определить напряжение между двумя любыми точками, рассчитав изменение потенциалов между ними. При этом нужно вести расчет в сторону увеличения потенциала, т. е. от второго индекса напряжения к первому.

Решим уравнение относительно тока:

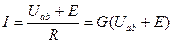где G = 1/R.АКОНЫ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Это выражение называют законом Ома для активной ветви. Последнее выражение можно составить исходя из следующих рассуждений. Для появления тока в ветви (рис. 2.2) есть два условия: наличие разности потенциалов между концами ветви и действие источника ЭДС. Если направления ЭДС и напряжения Uаb совпадают с направлением тока, они способствуют его появлению и должны быть записаны в уравнение со знаком плюс. В противном случае – со знаком минус. Рассуждая таким образом, получим для тока ветви прежнее выражение.

5. Баланс мощностей

Баланс мощностей – это интерпретация закона сохранения энергии в электротехнике. Мощность генераторов энергии в электрической цепи равна мощности потребителей: Pг = Рн, причем

,

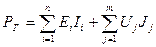где первое слагаемое – мощность источников ЭДС, а второе – мощность источников тка; J_j – токи источников тока; U_j – напряжения на зажимах источников тока.

Эти суммы алгебраические. Источник может как вырабатывать, так и потреблять электрическую энергию (заряд аккумулятора).

Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнении баланса мощностей с положительм знаком. Он работает в режиме генератора. При противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя). Определение знака мощности источника тока поясняет рис. 2.3, на котором показана разметка зажимов источника тока, вырабатывающего (а) или потребляющего (б) электрическую энергию.

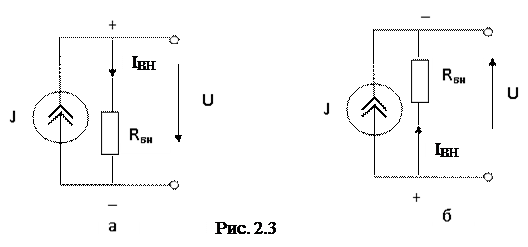Ток I_вн и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.

Мощность потребителей (нагрузок)

.

<1 2 345 6 7 >

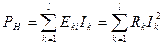Дата добавления: 2020-10-14; просмотров: 479;