Расчет простых ахроматоров
Условие получения системы с заданной оптической силой Φ и устранения хроматизма положения имеет вид:
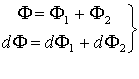 . (2.41)
. (2.41)
После преобразования (2.41) с учетом (2.39), получаем:
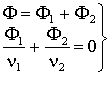 . (2.42)
. (2.42)
Решение системы уравнений (2.42) относительно Φ1 и Φ2 при заданных марках стекол дает следующий результат:
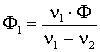 ,
,
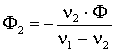 .
.
Объектив получается двух видов (рис. 2.60 (а, б)), если первая линза из крона, то объектив будет иметь вид, показанный на рис. 2.60 (а), а если первая линза будет из флинта, то будем иметь объектив по рис. 2.60 (б).
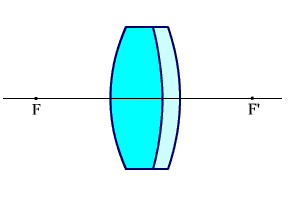 а) а)
| 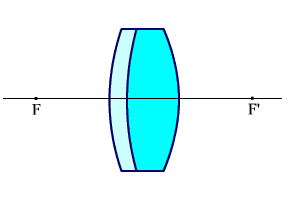 б) б)
|
Рис. 2.60. Простые ахроматы.
В тонком двухлинзовом объективе вместе с устранением хроматизма положения устраняется и хроматизм увеличения.
Симметричные оптические системы
Если оптическая система будет построена симметрично относительно AD и имеет β = -1, то автоматически исправляются кома, дисторсия и хроматизм увеличения (рис. 2.61).
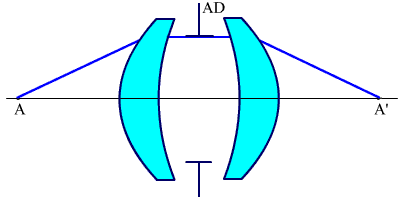
Рис. 2.61. Симметричная оптическая система.
Если предмет в бесконечности, то система, построенная по симметричному принципу, будет иметь небольшое значение комы, дисторсии и хроматизм увеличения.
Дата добавления: 2016-07-22; просмотров: 2562;











