Цилиндрические и торические линзы
Рассмотрим поверхности, не имеющие оси симметрии.
Поверхность, полученная вращением прямой линии вокруг параллельной неподвижной прямой, называется цилиндрической.
Поверхность, образованная вращением окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей ее, называется торической.
Пусть на линзу, имеющую плоскую и цилиндрическую поверхности, падает параллельный пучок лучей (рис. 2.65). В этом случае изображение получается не виде точки, а в виде прямой линии, длина которой равна длине линзы.
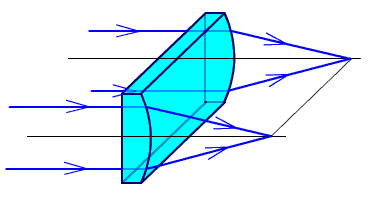
Рис. 2.65
Линза в двух взаимно перпендикулярных сечениях имеет различные оптические силы (рис. 2.66). В одном сечении ее действие аналогично действию сферической линзы, а в другом сечении она аналогична плоскопараллельной пластинке.
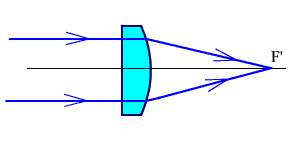 а) а)
|
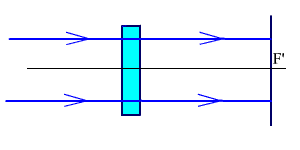 б) б)
|
Рис. 2.66
Если бы в линзе вторая поверхность была торической, то в одном и другом сечениях ее действие было бы аналогично действию сферических линз с различными фокусными расстояниями.
Цилиндрические и торические (в меньшей степени) линзы применяют в качестве очковых линз для исправления астигматизма. Астигматизм определяется разностью оптических сил в ее двух главных сечениях. Кроме этого цилиндрические линзы используются в таких системах, где нужно получить изображение в виде тонких протяженных линий.
Для некоторых областей техники (кинематографии) требуются оптические системы, создающие искаженные изображения. Особенно это важно при съемках высоких, но узких объектов или, наоборот, очень широких, но невысоких. При съемке таких объектов обычными объективами большая часть площади снимка остается неиспользованной. Необходимы системы, которые имеют разный масштаб изображения в двух взаимно перпендикулярных сеяниях. Такие системы называются анаморфоты.
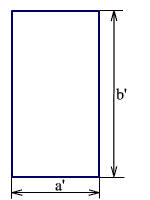
Анаморфотные системы создают изображения, трансформированные по высоте и ширине. На рис. 2.67 показан предмет (а) со сторонами a и b и его изображение, (б) со сторонами a' и b'.
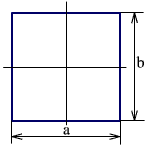 а) а)
|  б) б)
|
Рис. 2.67
При этом коэффициент ширины:
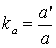 ,
,
коэффициент высоты:
 ,
,
коэффициент анаморфозы:
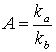 .
.
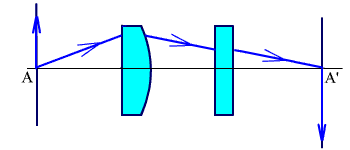
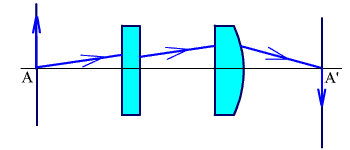
Пример построения анаморфотной системы дан на рис.2.68. В каждом сечении одна из цилиндрических линз действует, как обычная сферическая линза, другая, как плоскопараллельная пластинка. Плоскость предметов и изображений для двух сечений совпадают.
 а) а)
|
 б) б)
|
Рис. 2.68
Аксиконы
Аксиконы - это оптические элементы с большими сферической или хроматической аберрациями.
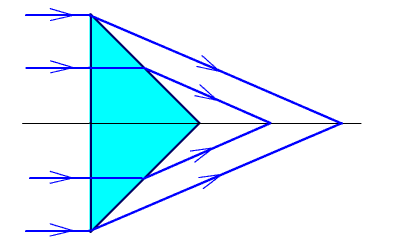
Они были созданы для устранения погрешности, возникающей при перефокусировке вследствие колебания визирной оси прибора. В результате больших аберраций точечный источник изображается в виде осевого отрезка большой длины, что позволяет при использовании аксикона не производить перефокусировку. Аксиконы используют также для обеспечения заданного распределения освещенности в плоскости изображения, а также компенсации нарушения гомоцентричности за счет действия других компонентов системы.
Примеры аксиконов показаны на рис. 2.69.
 а) а)
|  б) б)
|
Рис. 2.69. Аксиконы: (a) - коническая линза, (б) - положительный мениск
Единичный световод
Дата добавления: 2016-07-22; просмотров: 8049;











