Анаберрационные линзы с асферическими поверхностями

Если предмет находится в бесконечности, то линз со сферическими поверхностями, не имеющих сферической аберрации, нет.

Линзы без сферической аберрации при S = ∞ могут быть получены только с использованием асферических поверхностей. Две такие линзы, не имеющие совершенно сферической аберрации, показаны на рис. 2.62 и рис. 2.63. Линза, показанная на рисунке 2.62, - плоскогиперболическая.

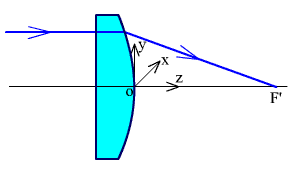
Рис. 2.62. Плоскогиперболическая линза.

У линзы, показанной на рис. 2.63, первая поверхность эллипсоидальная, имеющая ε = 1 / n, вторая поверхность концентрическая с центром кривизны в F'.

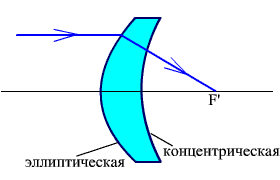
Рис. 2.63. Анаберрационная линза с эллипсоидальной первой поверхностью.

Плоские преломляющие поверхности

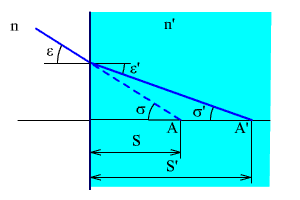
Рис. 2.48. Плоская преломляющая поверхность.

Сферическая аберрация плоской преломляющей поверхности (рис. 2.48) определяется по формуле:

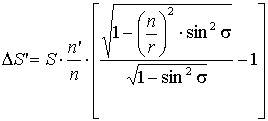. (2.24)

Если S < 0, то при n < n', ΔS' < 0 - сферическая аберрация отрицательная, при n > n' , ΔS' > 0 - сферическая аберрация положительная.

Сферическая аберрация плоско-параллельной пластинки всегда положительна