Сферическая преломляющая поверхность. Анаберрационные точки
Если предмет находится в бесконечности ( ∞). то сферическая преломляющая поверхность всегда имеет сферическую аберрацию. Если поверхность собирающая, то сферическая аберрация отрицательная, и наоборот, если поверхность рассеивающая, то сферическая аберрация положительная.
У каждой сферической поверхности есть три пары точек, в которых сферическая аберрация отсутствует. Эти точки называются анаберрационными.
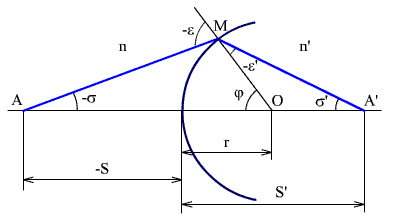
Рис. 2.49. Сферическая преломляющая поверхность.
Обратимся к рис. 2.49. Из ΔAMO следует:
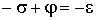 ,
,
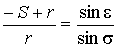 ,
,
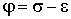 . (2.26)
. (2.26)
Из ΔOMA' получаем:
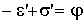 ,
,
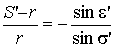 , (2.27)
, (2.27)
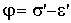 . (2.28)
. (2.28)
В общем случае при изменении угла σ отрезок S' меняется.
Из (2.27) получаем:
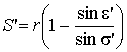 . (2.29)
. (2.29)
Условие отсутствия сферической аберрации:
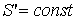 ,
,
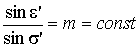 .
.
Поставленное условие может быть выполнено, если 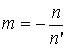 и
и 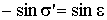 , так как
, так как 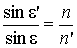 .
.
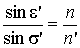 , (2.30)
, (2.30)
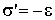 . (2.31)
. (2.31)
Подставляя (2.30) в (2.29), получаем:
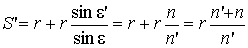 ,
,
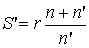 (2.32)
(2.32)
Используя инвариант Аббе для параксиальной области (2.33):
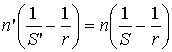 , (2.33)
, (2.33)
находим значение переднего отрезка S:
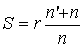 . (2.34)
. (2.34)
Приравнивая (2.26) и (2.28) и принимая во внимание σ' = -ε, получаем:
σ = -ε'. (2.35)
Следующая пара анаберрационных точек находится в центре кривизны поверхности. Лучи проходят не преломляясь, сферическая аберрация отсутствует: S = r, S' = r.
Третья пара анаберрационных точек находиться в вершине поверхности: S = 0, S' = 0.
Рассмотрим положение анаберрационных точек на примере (рис. 2.50).
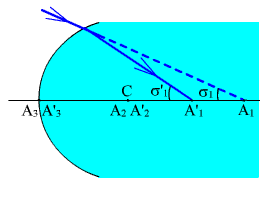
Рис. 2.50. Анаберрационные точки преломляющей поверхности.
Пусть r = 50, n = 1 и n' = 1.5182. Применяя формулы (2.32) и (2.34), получаем S = 125.91, S' = 89.93. Предметная точка A1 получилась мнимая, а точка изображения 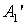 - действительная.
- действительная.
Вторая пара анаберрационных точек A2 и 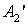 совпадает с центром кривизны C, S = S' = 50.
совпадает с центром кривизны C, S = S' = 50.
Третья пара A3 и 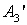 находятся в вершине поверхности S = S' = 0.
находятся в вершине поверхности S = S' = 0.
Определим линейное увеличение для трех пар аберрационных точек. На рис. 2.51 приведена идеальная оптическая система.
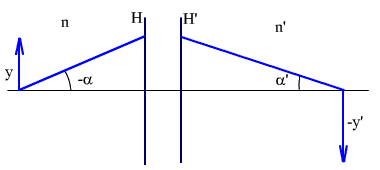
Рис. 2.51. Идеальная оптическая система.
Инвариант Лагранжа-Гельмгольца имеет вид:
n·α·y = n'·α'·y'. (2.36)
Линейное увеличение равно:
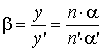 .
.
Для первой пары анаберрационных точек имеем:
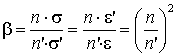 ,
,
n·ε = n'·ε'.
Для точки в вершине поверхности получаем:
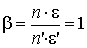 .
.
Для второй пары анаберрационных точек σ = σ' и увеличение равно:
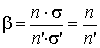 .
.
Дата добавления: 2016-07-22; просмотров: 3726;











