Расчет магнитных цепей постоянного тока

При расчете магнитной цепи решается одна из двух задач – прямая или обратная. При решении прямой задачи должны быть заданы магнитный поток в рабочем воздушном зазоре, размеры магнитопровода и материал магнитопровода, который должен быть задан в виде кривой намагничивания. Необходимо определить намагничивающую силу катушки.

При решении обратной задачи обычно бывают заданы намагничивающая сила, размеры и материал магнитопровода. Необходимо найти магнитный поток в рабочем воздушном зазоре.

Существует несколько методов для решения этих задач, а именно: графоаналитический метод, метод расчета по коэффициентам рассеяния и метод расчета по участкам. Для примера рассмотрим более подробно графоаналитический метод и метод по участкам.

5.5.1.Графоаналитический метод расчета магнитной цепи постоянного тока.

Прямая задача. Дано: поток в рабочем воздушном зазоре Ф_δ (рис. 57),размеры магнитной цепи, кривая намагничивания материала B(H).

Найти: намагничивающую силу катушки (Iw).

Порядок расчета. Магнитная цепь разбивается на участки с равномерным сечением и постоянной магнитной проницаемостью по всей длине участка. Так, в данном примере выделены такие участки: якорь, ярмо (корпус), основание и сердечник.

Задаются несколькими значениями потока в долях от заданного значения, например:

Ф₁=0.5Ф_δ; Ф₂=1.0Ф_δ; Ф₃=1.5Ф_δ.

Определяют индукцию на каждом участке магнитопровода от действия каждого из потоков

B=Ф/S, (130)

где S – площадь поперечного сечения участка

Рис. 57. К расчету магнитной цепи.

магнитной цепи По кривой намагничивания B(H) находят напряженность магнитного поля H_i на стальных участках магнитной цепи от действия каждого потока.

Определяют магнитное напряжение на каждом участке магнитной цепи от действия каждого потока

U_мстi= H_il_i – на стальных участках, (131) 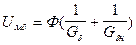– на воздушных зазорах. (132)

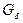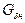Здесь l_i – средняя длина силовой линии магнитного потока на участке магнитной цепи; и – магнитные проводимости рабочего и нерабочего воздушных зазоров.

Определяется суммарное магнитное напряжение на стальных участках магнитопровода от действия каждого потока

U_мст1= H_с1l_с + H_я1l_я + H_к1l_к ; (133)

U_мст2= H_с2l_с + H_я2l_я + H_к2l_к ; (134)

U_мст3 = H_с3l_с+ H_я3l_я + H_к3l_к . (135)

Строятся зависимости Ф = f(U_мст) и Ф = f(U_мδ) (рис. 58).

Суммируя абсциссы функций Ф=f(U_мст) и Ф=f(U_мδ), получают результирующую кривую

Ф = f(U_м).

На оси ординат откладывают заданное значение потока Ф_δ и сносят на кривую Ф = f(U_м), получая на ней точку "a". Из точки "a" проводят луч к оси абсцисс под углом α, который определяется следующим образом

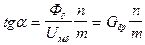, (136)

где n – масштаб по оси потока; m – масштаб по оси напряжений; 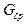– результирующая магнитная проводимость воздушных зазоров.

На оси абсцисс определяют искомое значение намагничивающей силы. Опустив перпендикуляр из точки a на ось абсцисс, легко определить составляющие этой намагничивающей силы, т. е.,

(Iw) = U_мδ + U_мст. (137)

Обратная задача решается аналогичным образом, а искомое значение магнитного потока находится из графика зависимости Ф=f(U_м) по заданной намагничивающей силе (Iw).

5.5.2. Распределение магнитных

Рис. 58. Графоаналитический потоков и напряжений в магнитной

метод расчета м.ц. цепи электромагнита. На рис. 59 показано распределение потока рассеяния и потока в сердечнике, а также магнитного напряжения по длине сердечника электромагнита, из которого видно, что поток рассеяния Ф_σ и поток в сердечнике Ф имеют параболическое распределение. Причем, на магнитной нейтрали поток рассеяния равен нулю, а поток в сердечнике максимален.

Магнитное напряжение по длине сердечника распределено по линейному закону и на магнитной нейтрали равно

нулю. Поток рассеяния между сердечником и ярмом распре-

Рис. 59. Эпюры распределения Ф и U_м делен по параболическому закону и на магнитной нейтрали равен нулю. Поток в сердечнике электромагнита распределен также по параболическому закону и на магнитной нейтрали он равен максимальному значению. Такое распределение потока рассеяния создает определенные трудности для его учета при расчете магнитной цепи. В связи с этим, магнитная цепь разбивается на участки не только по условию равномерности сечения и постоянства магнитной проницаемости, но и по условию равномерного распределения потока рассеяния по длине участка. То есть, параболическое распределение потока рассеяния на каждом участке заменяется линейным, равномерным по всей длине. Тогда можно считать, что поток рассеяния сосредоточен в середине участка и делит его пополам. Отсюда следует, что, чем более точным должен быть расчет магнитной цепи, тем на большее количество участков она должна быть разбита.

Для примера разобьем магнитную цепь (рис. 60) на такие участки: якорь, рабочий и нерабочий воздушные зазоры, сердечник, ярмо и основание. Кроме того, сердечник и ярмо разобьем еще на три участка, два из них над магнитной нейтралью и один под ней. Местоположение магнитной нейтрали определяется соотношением воздушных зазоров рабочего и зазора стыка основания с сердечником. Считаем, что поток рассеяния на каждом участке распределен равномерно, а на границах участков изменяется скачком.

Составим схему замещения (рис. 61).

Рис. 60. Деление магнитной цепи Причем, участки l₁, l₂ и l₃ сердечника

на участки и ярма представляем Т-образной схемой замещения (рис. 61, а), так как проводимость рассеяния на каждом из этих участков делит их пополам (согласно принятому условию).

Развернутую схему замещения (рис. 61, а) можно упростить, если учесть, что на участках между точками 1-2 и 2-3 действуют потоки неизменные по всей длине каждого участка, а меняются только на границах участков. В связи с этим, элементы схемы на этих участках можно объединить, т. е.

Рис. 61. Расчетные схемы замещения

(138) 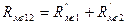; (139)

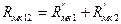; (140)

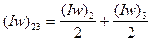; (141) 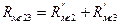; (142)

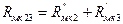. (143)

Таким образом, расчетная схема замещения рассматриваемой магнитной цепи приведена на рис. 61, б.

5.5.3. Расчет магнитных цепей методом участков.

Прямая задача. Дано: рабочий магнитный поток Ф_δ, размеры магнитной цепи, материал задан кривой намагничивания B(H). Найти намагничивающую силу катушки.

1) Определяем магнитное напряжение в якоре

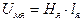, (144)

здесь l_я – длина средней магнитной линии в якоре; H_я – напряженность магнитного поля в якоре, которая определяется из кривой намагничивания B(H) по индукции в якоре B_я, где B_я= Ф_δ/S_я; S_я – площадь сечения якоря.

2) Определяем магнитное напряжение между точками 1–1

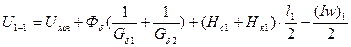. (145)

Значения H_с1 и H_к1 определяются аналогично H_я. При этом

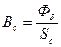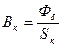, , (146)

S_с и S_к – площади сечений сердечника и ярма.

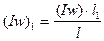, (147)

где l = l₁+l₂+l₃ – длина сердечника; (Iw) – намагничивающая сила катушки (искомая), которой предварительно можно задаться согласно выражению

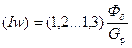. (148)

Здесь 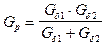– результирующая магнитная проводимость воздушных зазоров.

3) Определяем поток рассеяния 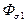и поток Ф₁ на участке l₁

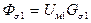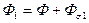, . (149)

Здесь 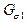– магнитная проводимость рассеяния

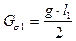. (150)

4) Магнитное напряжение между точками 2–2

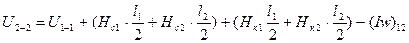. (151)

Здесь H_с2 и H_к2 – напряженности магнитного поля в сердечнике и ярме от действия потока Ф₁. Они определяются из кривой намагничивания по значениям индукции, найденным по формулам:

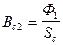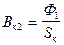, . (152)

5) Поток рассеяния 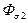и поток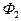

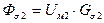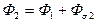, . (153)

6) Аналогично пп. 4 и 5 определяется магнитное напряжение между точками 3–3 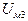, поток рассеяния 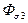и поток .

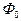7) Магнитное напряжение в основании ярма

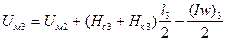. (154)

8) Нескомпенсированная часть МДС катушки

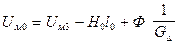, (155)

где H_о – напряженность магнитного поля в основании ярма, определяемая из кривой B(H) по индукции

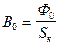. (156)

Если 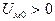, то это свидетельствует о том, что принятая предварительно МДС катушки недостаточна для создания необходимого магнитного потока Ф_δ и нужно задаться ее большим значением. В случае, если 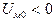, то принятая МДС больше необходимой и нужно задаться меньшим значением. Необходимо стремиться, чтобы погрешность, определяемая как 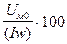%, не превышала (3…5)%.