МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННЫМИ

МАГНИТАМИ

Общие сведения

Постоянный магнит представляет собой брусок из стали или какого-либо другого ферромагнитного сплава, который, будучи намагниченным, устойчиво сохраняет запасенную часть магнитной энергии. Назначение магнита – служить источником магнитного поля, не изменяющимся под влиянием каких-либо внешних факторов. Постоянные магниты применяются в разнообразных устройствах и приборах: реле, электроизмерительных приборах, электрических машинах и др.

Различают следующие основные группы сплавов для постоянных магнитов:

1) мартенситовые стали – углеродистые, волфрамовые, хромистые, кобальтовые;

2) сплавы на основе стали – никеля – алюминия с добавлением в некоторых случаях кобальта и силиция: ални (Fe, Al, Ni), алниси (Fe, Al, Ni, Si), магнико (Fe, Ni, Al, Co);

3) сплавы на основе серебра, меди, кобальта.

Величинами, характеризующими постоянный магнит, являются остаточная индукция Br и коэрцитивная сила H_c (рис. 77). Для определения магнитных характеристик готовых магнитов пользуются кривыми размагничивания, представляющими собой зависимость B = f(-H).

Кривая снимается для кольца, которое сначала намагничивается до индукции насыщения, а затем размагничивается до B = 0 (рис. 77, а).

Магнитный поток в воздушном зазоре. Для использования энергии магнита необходимо изготовить его с воздушным зазором (рис. 77, б). Составляющая МДС, затрачиваемая постоянным магнитом на проведение потока в воздушном зазоре, называется свобод-

Рис. 77. Постоянный магнит ной МДС. Наличие воздушного зазора δ снижает индукцию в магните от B_r до B (рис. 77, б) аналогично тому как, если бы по катушке, надетой на кольцо (рис. 77, а), пропустили размагничивающий ток, создающий напряженность H. Это соображение положено в основу приведенного ниже способа вычисления потока в воздушном зазоре магнита.

При отсутствии зазора вся МДС расходуется на проведение потока через магнит:

(Iw)=H_cl_м B=Br,

где l_м – длина магнита.

При наличии воздушного зазора часть МДС (Iw)_δ будет расходоваться на проведение потока через зазор:

(Iw) = (Iw)_м + (Iw)_δ . (185)

Допустим, мы создали такую размагничивающую напряженность магнитного поля H, что Hl_м = (Iw)_δ и индукция при этом стала равной B.

При отсутствии рассеяния поток в магните равен потоку в воздушном зазоре

BS_м = (Iw)_δ G_δ , (186)

где S_м – площадь сечения магнита; G_δ = μ₀S_δ/δ – магнитная проводимость воздушного зазора; μ_o – магнитная проницаемость воздуха.

Из рис. 78 следует, что

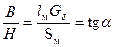. (187)

Рис. 78. Кривая размагничивания Таким образом, зная данные о материале магнита (в виде кривой размагничивания), размеры магнита l_м, S_м, и зазора δ и S_δ, можно вычислить поток в зазоре. Для этого следует провести на диаграмме (рис. 78) прямую Ob под углом α. Отрезок bc определяет индукцию В магнита. Отсюда поток в воздушном зазоре будет

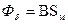. (188)

При определении tgα учитываются масштабы оси ординат и абсцисс:

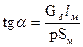, (189)

где p = n/m – отношение масштабов осей B и H.

С учетом рассеяния поток Ф_δ определяется следующим образом. Проводят прямую Ob под углом α, где tgα определяется по (191). Полученное значение В характеризует индукцию в среднем сечении магнита. Поток в среднем сечении магнита

. (190)

Поток в воздушном зазоре

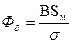, (191)

где σ – коэффициент рассеяния.

Индукция в рабочем зазоре

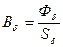. (192)

Прямые магниты. Выражение (192) дает решение задачи для магнитов замкнутой формы, где проводимости воздушных зазоров могут быть вычислены с достаточной для практических целей точностью. Для прямых магнитов задача вычисления проводимостей потока рассеяния весьма трудна. Поток вычисляется с помощью опытных зависимостей, связывающих напряженность поля магнита с размерами магнита.